
TeorVer / 1. Задачи на классическую вероятность
.pdf
1. ЗАДАЧИ НА КЛАССИЧЕСКУЮ ВЕРОЯТНОСТЬ
В качестве численной меры степени объективной возможности случайного события используется вероятность события. Под случайным событием понимается всякий факт, который в результате опыта со случайным исходом может произойти или не произойти. Для полной группы равновозможных и несовместных событий возможен непосредственный подсчет вероятностей по "классической" формуле:
P( A) mnA ;
где: mA – число случаев благоприятных событию A ; n – общее чис-
ло случаев.
Геометрическая вероятность определяется следующим образом. В результате испытания в некоторой области S появляется точка. Вероятность попасть в какую-либо часть области S пропорциональна мере этой части (длине, площади, объему) и не зависит от ее расположения и
формы. Таким образом, если s |
– часть области S , то вероятность со- |
||
бытия A – попасть в область s |
– равна |
||
P( A) |
мера s |
. |
|
|
|
||
|
мера S |
|
|
Так как совокупность всех точек области S бесконечна, то "геометрическую вероятность» можно рассматривать как обобщение понятия "классической вероятности" на случай испытаний с бесконечным числом исходов.
Частотой (частостью) события А в опыте, состоящем из серии испытаний, называется отношение числа испытаний, в кот о- рых появилось событие А, к общему числу испытаний. Частоту
4
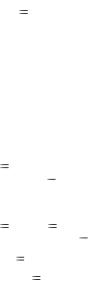
события иногда называют статистической вероятностью и вычисляют по следующей формуле:
* |
|
M A |
|
|
P |
( A) |
|
, |
|
N |
||||
|
|
|
где: M A – число появлений события А в опыте, N – общее число про-
изведенных испытаний.
При вычислении вероятностей по классической формуле часто используются сочетания, размещения и перестановки. Два сочетания отличаются друг от друга хотя бы одним элементом, а размещения отличаются либо самими элементами, либо порядком их следования.
Число сочетаний из п элементов по m вычисляется по формуле
Cm |
n! |
|
, |
|
|
||
n |
m!(n |
m)! |
|
|
|||
а число размещений из п элементов по т:
Am |
Cmm! |
|
n! |
. |
|
|
|||
|
|
|||
n |
n |
(n |
m)! |
|
|
|
|
При n m размещения представляют из себя перестановки из п элементов: Pn n!.
ЗАДАЧИ ДЛЯ АУДИТОРНЫХ ЗАНЯТИЙ
1.1. Из слова "НАУГАД" выбирается наугад одна буква. Какова вероятность того, что: а) это буква "Я"; б) это гласная?
Ответ: а) 0; б)1/2
1.2. В урне имеются 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар:
а) белый; б) черный?
Ответ: а) 3/10; б) 7/10
1.3. При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов?
Ответ: 30
1.4. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что извлеченный наудачу кубик будет иметь две окрашенные грани.
Ответ: 0,096
5

1.5. Брошены три монеты. Найти вероятность того, что выпадут два "герба".
Ответ: 3/8
1.6. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что обрыв произошел между 50-м и 55-м километрами линии?
Ответ: 1/6
1.7. Бросают "правильную" игральную кость. Какова вероятность выпадения номера 5 на верхней грани упавшей на стол кости? Какова вероятность выпадения номера большего или равного 5? ("Правильная" игральная кость представляет собой кубик, грани которого отмечены номерами 1, 2, 3, 4, 5, 6, и сумма чисел на любых двух противоположных гранях равна 7.)
Ответ: 1/6; 1/3
1.8. В партии транзисторов n стандартных и m бракованных. При контроле оказалось, что первые k транзисторов стандартны. Найти вероятность того, что следующий транзистор будет стандартным.
Ответ: p (n k) (n m k)
(n m k)
1.9. Брошены две игральные кости. Какова вероятность выпадения на двух костях в сумме не менее 9 очков? Какова вероятность выпадения единицы, по крайней мере, на одной кости?
Ответ: 5/18; 11/36
1.10. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово "ДВА"?
Ответ: 1/60
1.11. На шахматную доску из 64 клеток наугад ставятся две ладьи разного цвета. Какова вероятность, что они не будут "бить" друг друга?
Ответ: 7/9
1.12. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся черными?
Ответ: 7/15
1.13. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.
Ответ: 1/20
6

1.14. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 студентов третьего курса. Из этого состава выбирают 5 человек. Найти вероятность, что: а) все первокурсники попадут в совет; б) в совет будет избран 1 первокурсник, 2 второкурсника и 2 студента третьего курса.
Ответ: а) 2/91; б) 30/143
1.15. В партии из 50 изделий 5 бракованных. Из партии выбираются наугад 6 изделий. Определить вероятность того, что и среди 6 изделий 2 окажутся бракованными.
Ответ: 0,0938
1.16. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.
Ответ: 0,00005372
1.17. В лифт 8-этажного дома на первом этаже вошли 5 человек. Предполагая, что каждый из них с равной вероятностью может выйти на любом из этажей, начиная со второго, найти вероятность того, что все пятеро выйдут на разных этажах.
Ответ: 0,15
1.18. Имеются r шаров, которые случайным образом разбрасываются по n ящикам. В одном и том же ящике могут находиться несколько шаров, и даже все шары. Найти вероятность того, что в первый ящик попадут ровно r1 шаров, во второй – r2 шаров и т.д., в n-й – rn
шаров, r1 r2 rn r .
Ответ: r! nr r1!...rn!
1.19.Два человека A и B условились встретиться между четырьмя
ипятью часами. Пришедший первым ждет второго в течение 10 минут, после чего уходит. Чему равна вероятность встречи, если приход каждого человека в течение указанного часа может произойти в любое время?
Ответ: 11/36
1.20. Газ, состоящий из n молекул, находится в замкнутом сосуде. Мысленно разделим сосуд на n равных клеток и будем считать, что вероятность каждой молекулы попасть в каждую из n клеток одна и та
7

же, а именно, 1/ n . Какова вероятность того, что молекулы окажутся распределенными так, что в первой клетке окажется m1 молекул, во
второй – m2 молекул, в n-й – mn молекул?
Ответ: P n! nnm1!m2!... mn!
Задача того же типа, что и 1.18 о распределении шаров по ящикам. Клетки играют роль "ящиков", а молекулы "шаров". Вероятность P при
заданном n достигает максимума при m1 |
m2 mn |
1, т.е. при |
равномерном распределении молекул. Например, при n |
100 вероят- |
|
ность равномерного распределения молекул |
равна 9,3 10 43 (очень |
|
мала) |
|
|
1.21. (Задача Бюффона, 1777 г.) На пол, разграфленный параллельными прямыми на полосы ширины L, бросается наугад игла длиной l (l<L). Найти вероятность того, что игла пересечет какую-нибудь прямую.
Ответ: 2l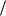 L
L
ЗАДАЧИ ДЛЯ ДОМАШНИХ ЗАДАНИЙ И САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.22. В 25 экзаменационных билетах содержится по два не повторяющихся вопроса. Студент знает ответы только на 45 вопросов. Какова вероятность того, что вытянутый экзаменующимся билет состоит из подготовленных вопросов?
Ответ: 0,8
1.23. Из последовательности чисел 1, 2, ..., n наугад выбираются два числа. Какова вероятность того, что одно из них меньше k, а другое больше k, где 1 k n
Ответ: 2(k 1)(n k) / n(n 1)
1.24. В лотерее разыгрывается 1000 билетов. Среди них два выигрыша по 5000 руб., пять выигрышей по 2000 руб., десять выигрышей по 1000 руб. и 25 по 500 руб. Некто покупает один билет. Найти вероятность: а) выигрыша не менее 2000 руб.; б) какого либо выигрыша.
Ответ: а) 0,007; б) 0,042
8

1.25. A и B и еще 8 человек стоят в очереди. Определить вероятность того, что A и B отделены друг от друга тремя лицами.
Ответ: 2/15
1.26. В чулане находятся n пар ботинок. Из них случайно выбираются 2r ботинок (2r<n). Какова вероятность того, что среди выбранных ботинок: а) отсутствуют парные; б) имеется ровно одна комплектная пара; в) имеются ровно две комплектные пары?
Ответ: а) C2r 22r |
C2r ; б) n 22r |
2 C2r 2 |
C2r |
; |
|
n |
2n |
|
n 1 |
2n |
|
|
в) C2 |
22r 4 C2r 4 |
C2r |
|
|
|
n |
|
n 2 |
2n |
|
1.27. Среди 25 экзаменационных билетов 5 "хороших". Два студента по очереди берут по одному билету. Найти вероятности следующих событий: A={первый студент взял хороший билет}; B={второй студент взял хороший билет}; C={оба студента взяли хорошие билеты}.
Ответ: P(A)=1/5; P(B)=1/5; P(C)=1/30
1.28. На бесконечную шахматную доску со стороной квадрата a бросается наудачу монета диаметром 2r<a. Найти вероятность того, что: а) монета попадет целиком внутрь одного квадрата; б) монета пересечет не более одной стороны квадрата.
Ответ: а) (a 2r)2 / a2 ; б) 1 4r2 / a2
1.29. В партии из 20 радиоприемников 5 неисправных. Для проверки наугад обирается 3 радиоприемника. Найти вероятность того, что в число выбранных войдут один неисправный и два исправных приемника.
Ответ: 35/76
1.30. Какой толщины должна быть монета радиуса R, чтобы вероятность падения на ребро была бы равна 1/3?
Ответ: 0,707R
1.31. Из телефонной книги выбирается случайный номер. Считая, что все номера состоят из 7 цифр, причем все комбинации цифр равновероятны, найти вероятность того, что все цифры номера различны.
Ответ: 0,0605
9

1.32. Группа, состоящая из 8 человек, занимает места за круглым столом случайным образом. Какова вероятность того, что два определенных лица окажутся сидящими рядом?
Ответ: 2/7
1.33. Монета бросается до тех пор, пока два раза подряд не выпадет одной и той же стороной. Каждому возможному исходу, требую-
щему n бросаний, припишем вероятность 2 n . Описать пространство элементарных событий. Найти вероятность следующих событий: а) опыт окончится до 6-го бросания; б) потребуется четное число бросаний.
Ответ: Пространство элементарных событий: ГГ, РР, РГГ, ГРР,...;
а) 15/16; б) 2/3
1.34. Самолет, имеющий радиолокационную станцию с дальностью действия d, осуществляет поиск со скоростью v в достаточно большом районе площадью S, в любой точке которого может находиться в течение времени t подводная лодка. Найти вероятность обнаружения подводной лодки, если время t невелико и лодка обнаруживается при попадании в зону действия радиолокатора.
Ответ: ( d 2 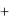
1.35. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равно возможно в течении суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, а второго — два часа.
Ответ: 139/1152
1.36. Два лица независимо друг от друга имеют равную вероятность прийти в метро в любой момент промежутка времени T. Найти
вероятность того, что время ожидания одним другого будет меньше t
(0 t T) .
Ответ: 1 (1 t / T )2
1.37. n человек садятся случайным образом за круглый стол. Найти вероятность того, что: а) два фиксированных лица A и B сядут рядом, причем B слева от A; б) три фиксированных лица A, B и C сядут ря-
10
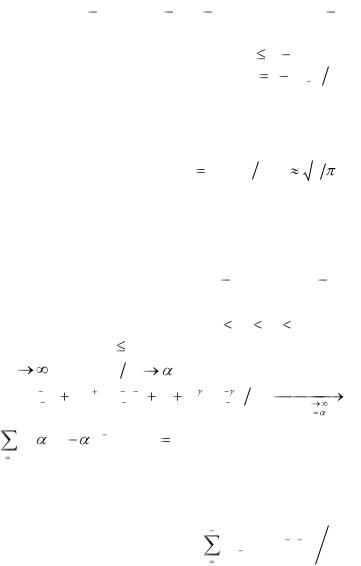
дом, причем A справа от B, а C слева; в) Найти те же вероятности в случае, когда люди садятся по одну сторону прямоугольного стола.
Ответ: а) 1/(n 1) ; б) 1/(n 1)(n 2) ; в) 1/ n , 1/ n(n |
1) |
||
1.38. В лотерее n билетов, из которых m выигрышные. Какова ве- |
|||
роятность выигрыша для того, кто купит k билетов, k |
n |
m ? |
|
Ответ: p |
1 |
Ck |
Ck |
|
|
n m |
n |
1.39. Группа, состоящая из 2N мальчиков и 2N девочек, делится случайным образом на две равные части. Найти вероятность того, что в каждой части число мальчиков и девочек одинаково. Вычислить эту
вероятность, используя формулу Стирлинга. |
|
|
|
Ответ: p (C N |
)2 |
C2 N |
|
2 N |
|||
2 N |
|
4 N |
|
1.40. Каждая из n палок разламывается на две части – длинную и короткую. Затем 2n полученных обломков объединяются в n пар, каждая из которых образует новую "палку". Найти вероятность того, что: а) все обломки объединены в первоначальном порядке; б) все длинные части соединены с короткими.
Ответ: а) 1/(2n 1)!!; б) n!/(2n 1)!!
1.41. Из последовательности чисел 1, 2, ..., N отобраны наудачу n чисел и расположены в порядке возрастания: x1 x2 xn . Како-
ва вероятность того, что xm |
M ? |
Найти предел этой вероятности, |
|
когда M, N |
так, что M N |
>0. |
|
m n m |
|
m 1 |
n m 1 |
Ответ: CM CN M |
|
CM CN M |
|
n |
|
|
|
Ck k |
(1 |
)n |
k , где γ |
n |
|
|
|
... CM CNn |
M CNn |
M , N |
|
|
M / N |
min{n,M}
km
1.42.Найти вероятность того, что при раздаче колоды в 52 карты четырем игрокам первый из них получит ровно n пар "туз–король одной масти".
4 |
n |
|
|
|
Ответ: Cn |
Ck |
2k C13 |
k 2n |
C13 |
4 |
4 n |
44 |
|
52 |
k |
0 |
|
|
|
11
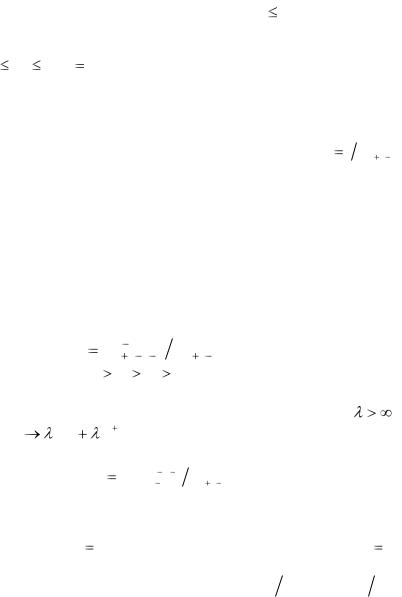
1.43. В статистической механике рассматриваются системы, состоящие из r неразличимых частиц и n ячеек, r n , каждая из частиц попадает в одну из ячеек. Состояние такой системы описывается как распределение r частиц по n ячейкам и определяется набором чисел
0 mi r (i 1, 2, , n) , где mi – число частиц в i-й ячейке. Фотоны, атомные ядра и атомы, содержащие четное число элементарных частиц, подчиняются статистике Бозе – Эйнштейна, в которой рассматриваются только различные состояния и каждому из них приписывается равная вероятность. Найти ее.
Ответ: p 1 Cr |
r 1 |
n |
1.44. Электроны, протоны, нейтроны подчиняются статистике Ферми – Дирака, в которой предполагается, что, во-первых, в одной ячейке не может находиться более одной частицы; и, во-вторых, все различные состояния, удовлетворяющие первому условию, имеют равную вероятность. Найти эту вероятность в случае, когда имеется r частиц и n ячеек.
Ответ: См. задачу 1.43
1.45. Пусть имеется r частиц и n ячеек, причем имеет место статистика Бозе – Эйнштейна (см. задачу 1.43).
1) Доказать, что вероятность нахождения в фиксированной ячейке k
частиц равна qk |
r |
k |
|
r |
r 1 . |
Cn |
r |
k 2 |
Cn |
||
2) Показать, что q0 |
q1 |
|
q2 |
. |
|
3) Доказать, что если n и r неограниченно возрастают, причем среднее
число частиц r/n, приходящихся на одну ячейку, стремится к |
, |
||
то q |
k /(1 |
)k 1 . |
|
k |
|
|
|
4) Доказать, что вероятность того, что ровно m ячеек останутся сво-
бодными, равна p |
m |
CmCn m 1 |
C r |
. |
|
n r 1 |
n r 1 |
|
1.46. Если при распределении r частиц по n ячейкам все nr распределений будут иметь равную вероятность, то говорят о статистике Максвелла – Больцмана (см. задачи 1.43 и 1.45). Найти вероятность то-
го, что: а) при n r ни одна ячейка не останется пустой; б) при n |
r |
останется пустой только одна ячейка. |
|
Ответ: а) n! n r ; б) n!Cn2 |
n r |
