

7. Сравнение интеграла
Лебега с интегралом Римана
Теорема 1 (Лебег). Если для
функции f, заданной на отрезке
[a,b], существует собственный
интеграл Римана, то она интегрируема по Лебегу и ее интеграл Лебега равен интегралу Римана.
Доказательство.
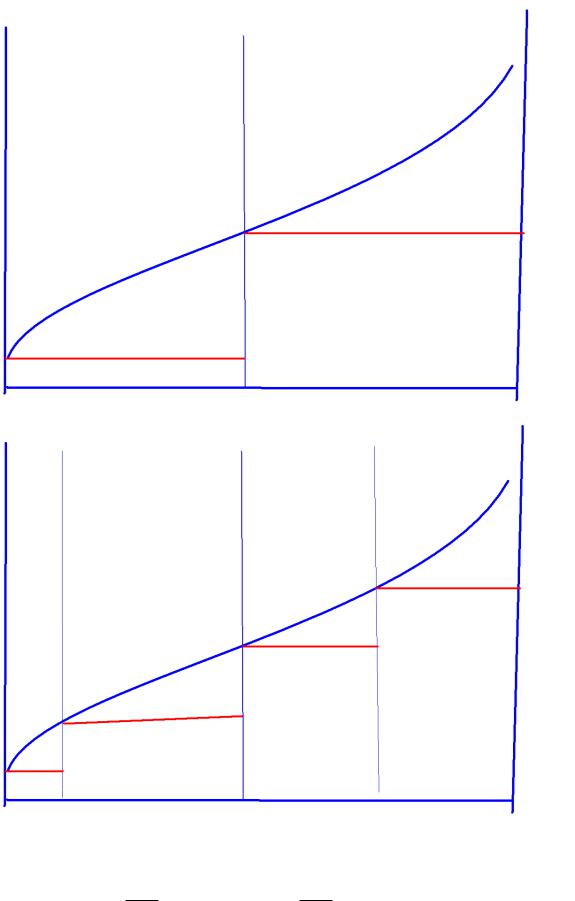
Построим верхнюю и нижнюю
суммы Дарбу для интеграла
Римана. Фиксируем n и отрезок [a,b]
разбиваем на 2n частей точками xk = a + (k/2n)·(b-a), 0≤k≤2n.

Пусть
M nk sup f (x), |
mnk |
inf f (x) |
xk 1 x xk |
|
xk 1 x xk |
Тогда верхняя и нижняя суммы Дарбу определяются равенствами
|
|
2n |
b a |
|
||||
Sn M nk |
|
|||||||
|
|
|
|
|
|
|||
|
|
2 |
n |
|
||||
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
b a |
||
|
|
S n |
|
|
m |
|||
|
|
|
|
|||||
|
2n |
|||||||
|
|
|
|
|
nk |
|||
|
|
|
|
|
k 1 |
|
||
Построим функции
f n (x) M nk , если xk-1≤x<xk; f n (x) mnk , если xk-1≤x<xk.
Это простые функции и
|
n |
|
|
|
|
n (x)d |
S |
|
f |
||||
|
|
[a,b] |
||||
S n |
|
f |
n (x)d |
|||
|
|
|
||||
|
|
[a,b] |
||||
Последовательность f n (x)
монотонно возрастает:
f n (x) f n 1 (x)
Последовательность f n (x)
монотонно убывает:
f n (x) f n 1 (x)
f n (x) f n 1 (x)
Поэтому существуют пределы
lim f (x) f (x) f (x)
n n
lim f n (x) f (x) f (x)
n
f
Так как
f
n
n
(x) sup f (x)
(x) sup f (x)
то по теореме Лебега о
предельном переходе
f (x) и f (x)
– интегрируемые по
Лебегу функции и
|
|
|
|
(x)d lim |
|
|
|
n (x)d lim |
|
n |
||
|
f |
|
f |
S |
||||||||
|
|
|
|
n |
|
|
|
|
|
n |
||
[a,b] |
|
[a,b] |
|
|
|
|||||||
|
f |
(x)d lim |
|
f |
n |
(x)d limS n |
||||||
|
|
n |
||||||||||
[a,b] |
|
n |
[a,b] |
|||||||||
|
|
|
|
|
||||||||

Поскольку функция f интегрируема по Риману, то
|
|
|
|
|
|
|
|
b |
|||||||
|
|
|
lim S n |
f (x)dx I |
|||||||||||
lim S n |
|||||||||||||||
n |
|
n |
a |
||||||||||||
|
|
|
|
|
|
|
|
||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim f |
n (x) f |
(x) d |
|||||||||||||
n [ a,b] |
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f |
(x) f (x) d 0 |
|||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
[ a,b] |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
(x) f (x) |
||||||||||
и значит почти всюду |
f |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(x) f (x) f (x) |
|||||||||||||
Но |
f |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому f(x) интегрируема по Лебегу и
f (x)d I |
■ |
|
[a,b]

Теорема 2. Ограниченная
функция f, заданная на отрезке
[a,b], интегрируема по Риману
тогда и только тогда, когда
множество ее точек разрыва имеет меру нуль.
Пусть f интегрируема по Риману.
Тогда по теореме 1 почти всюду
выполняется равенство f (x) f (x)
Зафиксируем точку x0 и выясним,
что означает равенство f (x0 ) f (x0 )
|
|
|
|
|
|
|
0 n( ) : |
|
f n (x0 ) f |
(x0 ) |
|
||
|
|
|
|
|
n |
|
|
|
|
|
|
||
Пусть x0 оказалась внутренней
точкой интервала (α,β), полученного
при разбиении отрезка [a,b] на 2n
частей. Тогда

( , ) |
( , ) |
f (x) |
sup f (x) inf |
||
f (x) f (x0 ) x ( , )
Значит, функция f непрерывна в
точке x0. В результате непрерывность функции f доказана для всех точек, кроме точек разбиения отрезка (вида k/2n) и точек, где f (x0 ) f (x0 )
Таким образом, функция f
непрерывна почти всюду
Упражнение 1. Проводя рассуждения в обратном порядке, доказать, что если функция f непрерывна почти
всюду, то f (x) f (x)
почти всюду. (Тогда функция f |
■ |
|
интегрируема по Риману.) |
||
|

Теорема 3. Пусть функция f
интегрируема по Риману на любом
отрезке [a,b-ε]. Тогда функция f
интегрируема по Лебегу на
отрезке [a,b] тогда и только тогда, когда ее несобственный интеграл Римана 2 рода сходится
абсолютно.
Теорема 4. Пусть функция f
определена на луче [a,) и
интегрируема по Риману на любом
отрезке [a,b]. Тогда функция f
интегрируема по Лебегу на луче [a,)
тогда и только тогда, когда ее несобственный интеграл Римана
1 рода сходится абсолютно.

Упражнение 2. Привести пример
неограниченной функции f,
которая не интегрируема по Лебегу на отрезке [a,b], но ее несобственный интеграл Римана 2 рода сходится.
