Курсовая работа / Вариант 33 - Богданова - 2006 / вар 33

В ста случаях зарегистрировано время проведения синтеза на химическом производстве. Результаты регистрации сведены в таблицу:

27	51	107	21	20	46	35	27	6	25
16	118	3	3	0	54	85	30	39	43
15	59	3	143	70	10	82	71	64	67
17	29	43	285	3	17	185	42	26	3
88	22	31	6	25	0	29	170	242	22
31	79	117	0	101	55	3	38	13	16
42	316	0	32	52	102	7	63	24	68
67	29	17	4	21	96	112	91	26	9
167	7	58	132	21	20	28	0	5	26
20	58	65	96	19	42	99	30	79	65

Содержание курсовой работы по стандартизации.

1. найти оценку математического ожидания и дисперсии случайной величины Х;

2. найти доверительный интервал для математического ожидания и дисперсии соответствующей заданной доверительной вероятностью;

3. оценить вероятность попадания случайной величины Х в заданный интервал;

4. для этой вероятности из п. 3 найти доверительный интервал, соответствующий заданной доверительной вероятности (1-);

5. построить гистограмму и эмпирическую формулу распределения случайной величины Х;

6. найти и построить доверительную область для плотности распределения f(x) и функции распределения F(x), соответствующие заданной доверительной вероятности;

7. сгладить гистограммы и эмпирическую функцию распределения подходящим законом;

8. используя χ² проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом при заданном уровне значимости α.

Решение

1. Выборочное среднее:

=53,22, где n – общее число значений п=100, x_i – значения

Исправленная дисперсия:

=6147,98

Выборочная дисперсия:

=6086,50

2. 1-α →2Ф(ε_α)=1-α

Две функции равны доверительному интервалу

Функция Ла-Пласа.

=0,4

По таблице значений функции Ла-Пласа находим ε_α = 1,29

Доверительный интервал для математического ожидания:

43,11<Mx<63.33

Доверительный интервал для дисперсии:

5182.74<Dx<7493.29

Интервал (0,6÷1)

31.93<X<53.22

=0.13- частота попадания случайных величин в заданный интервал,

m= 13– сколько значений попало в интервал

4. Доверительный интервал для вероятности

Для 1-α=0.85, ε=1,42, находим 0,089<P<0.185

Заключим все экспериментальные данные в интервал от минимального до максимального значения. Поделим этот интервал на равные разряды по 10.

Таблица 2.

Разряд ( Хi-1,Хi )	Частота попадания случайной величины Х в разряд ( Хi-1,Хi )	Значение гистограммы
( 0;31,6 )	0,5	0,01582
( 31,6;63,2)	0,19	0,00601
( 63,2;94,8)	0,14	0,00443
( 94,8;126,4)	0,09	0,00285
( 126,4;158 )	0,02	0,00063
( 158;189,6 )	0,03	0,00095
( 189,6;221,2 )	0	0
( 221,2;252,8 )	0,01	0,00032
( 252,8;284,4 )	0	0
( 284,4;316 )	0,02	0,00063

Интервал от 1 до 101 делим на 10 частей

n_i – число значений, попавших в этот разряд. Δх – длина разряда

График гистограммы

6. Порядок построения доверительной области для функции распределения.

В данном случае общее число разрядов r равно 10 плюс один полубесконечный разряд, r = 11. Если теперь выбрать доверительную вероятность (1 - ) равную 0,90,то по формуле получим .

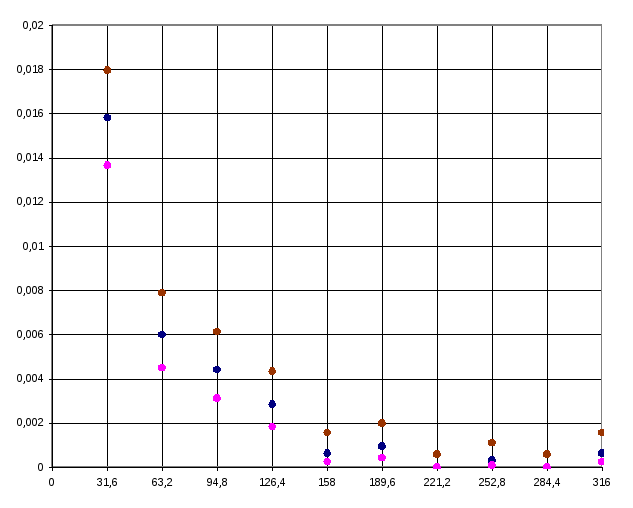
Результирующие доверительные границы для плотности на каждом разряде гистограммы представлены в таблице.

Разряд ( Хi-1,Хi )	Доверительные границы для плотности распределения
(0;31,6)	0,013675……0,017970
(31,6;63,2)	0,004499……0,007888
(63,2;94,8)	0,003135……0,006145
(94,8;126,4)	0,001835……0,004339
(126,4;158)	0,000249……0,001576
(158;189,6)	0,000441……0,002006
(189,6;221,2)	0,000000……0,000583
(221,2;252,8)	0,000088……0,001116
(252,8;284,4)	0,000000……0,000583
(284,4;316)	0,000249……0,001576
(316;379,2)	0,000000……0,000292

Рис: Гистограмма с доверительными интервалами.

Далее по таблице распределения величины (распределение Колмогорова) находим ее величину, соответствующую коэффициенту доверия (1 - ) = 0.90. Она равна = 1.36.

Затем по формуле (15) рассчитываем доверительную область для функции распределения :

где

График этой области представлен на рис.

Рис: Эмпирическая функция распределения

с доверительной областью.

7. Гистограмма

Из формы гистограммы следует, что гипотетическим распределением может быть экспоненциальное распределение с функцией

и с плотностью

где - оценка неизвестного истинного значения. Т.к. , то и, следовательно,

и

Задание 8. χ² – критерий Пирсона.

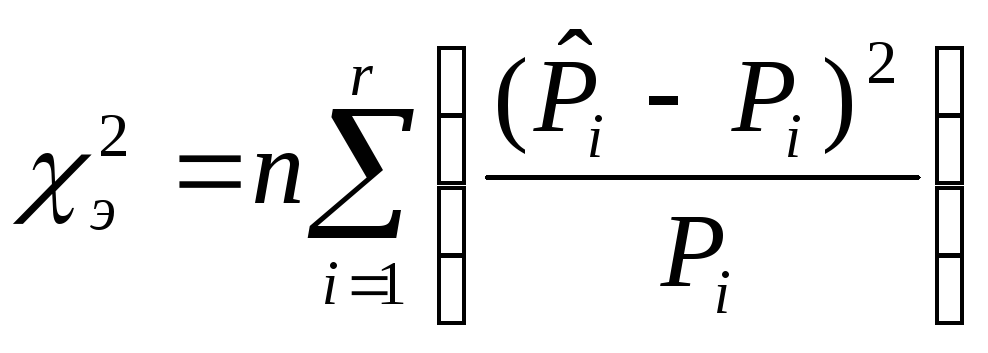, где χ_э² – экспериментальный критерий Пирсона.

Для нормального распределения

Для проверки гипотезы выберем уровень значимости  = 0,05 и используем вначале критерий согласия. Его экспериментальное значение равно.

А его гипотетическое значение при выбранном уровне значимости  = 0.05 и числе степеней свободы s = 11 - 1 - 1 = 9, согласно условию (20) равно . Таким образом, и, следовательно критерий Пирсона не подтверждается. Вывод: гипотеза по критерию согласия является неправдоподобной.

Российский химико-технологический университет им. Д.И.Менделеева

Курсовая работа

Статистическая обработка экспериментальных данных при сертификации продукции

Оценка распределений и параметров

Выполнила:

студентка гр. Ф-41

Галузина Светлана

Преподаватель:

Иванов В.В.

Москва

2006