
Кравчук(mathcad) / 1 семестр / Visual_Basic_6.0._Посiбник_2009
.pdf3.4. Запитання для самоконтролю
1.Як створювати масиви управляючих елементів?
2.Для чого використовується нестандартний управляючий елемент
MSFlexGrid?
3.Дайте визначення масивів. Що таке індекс? Як його можна задати?
4.Які види масивів (за виміром) ви знаєте?
5.Для чого використовується оператор Option Base 1?
6.Для чого використовуються оператори Dim та ReDim? Синтаксис операторів.
7.Яка різниця між статичними та динамічними масивами?
Програмування типових алгоритмів обробки одновимірних масивів.
8.Одновимірні масиви. Які способи введення елементів масиву ви знаєте?
9. . Одновимірні масиви. Які способи виведення елементів масиву ви знаєте?
10.Як сформувати елементи одновимірного масиву в діапазоні цілих чисел на довільному проміжку за допомогою генератора випадкових чисел Rnd?
11.Як обчислити суму та кількість елементів (усіх або за умовою)?
12.Як обчислити добуток та кількість елементів (усіх або за умовою)?
13.Як знайти найменший елемент та його номер серед елементів масиву (усіх або за умовою)?
14.Як знайти найбільший елемент та його номер серед елементів масиву (усіх або за умовою)?
15.Як обчислити середнє арифметичне та середнє геометричне?
16.Як сформувати з існуючого масиву окремий масив по заданій умові?
17.Як відсортувати елементи масиву відповідно заданих умов (за спаданням, за зростанням)?
Програмування типових алгоритмів обробки двовимірних масивів.
18.Двовимірні масиви (таблиці). Які способи введення елементів масиву ви
знаєте?
19. .Двовимірні масиви. Які способи виведення елементів масиву ви знаєте?
20.Як сформувати елементи двовимірного масиву в діапазоні цілих чисел на довільному проміжку за допомогою генератора випадкових чисел Rnd?
21.Яка відмінність типових алгоритмів обробки двовимірних масивів від одновимірних, що перераховані в пунктах 11-16?
22.Як виконати обчислення в таблицях по рядках (стовпцях)?
23.Що таке транспонування матриці?
24.Як здійснити транспонування матриці?
25.У чому переваги модульного програмування? Як добавити модуль до проекту?
26.Для чого використовується процедура типу Function? Як створити таку процедуру?
27.Яка різниця між формальними параметрами та фактичними аргументами?
28.Як звернутися до процедури Function?
29.Для чого використовується процедура типу Sub? Як створити процедуру?
30.Як звернутися до процедури типу Sub?
170
3.5. Самостійна робота студентів (СРС-6...9)
Студенту надається можливість вибрати тип виконуваної СРС (теоретична, або практична).
За кожну виконану теоретичну СРС виставляється 1 бал, за захист відповідної теоретичної СРС додається ще 1 бал. За правильне виконання практичної СРС виставляється 3 бала, за захист відповідної практичної СРС додається ще 1 бал.
3.5.1. Теоретичні завдання для виконання самостійної роботи
ЗМІСТ СРС-6.
Функції форматування виводу мови Visual Basic
6.1.Tab(n)
6.2.Spc(n)
6.3.String$(n,” символ ”)
6.4.Format(<Вираз>[, <Формат>])
6.5.Chr(<Код символа>)
ЗМІСТ СРС-7
Оператори управління
7.1. Порівняння операторів циклу For…Next, While…Wend, Do…Loop.
ЗМІСТ СРС-8
Складні типи даних
8.1.Порівняння операторів Dim та ReDim.
8.2.Функція Array.
ЗМІСТ СРС-9
Засоби створення складних програм
9.1.Порівняння підпрограм – процедур типу Sub…End Sub
та функцій – процедур типу Function…End Function.
Вимоги до оформлення теоретичної СРС
Вимоги для оформлення аналогічні вимогам щодо СРС-4, 5 (див. 2.6.1).
3.5.2. Практичні завдання для виконання самостійної роботи
Скласти схему та програму. Формування матриць виконати за допомогою генератора випадкових чисел Rnd у вигляді підпрограми.
171
№1
Задано дві матриці А та В розмірності n n (n = 4). Знайти компоненти век-
тора z (zi = xi+ yi), де
xi – різниця максимального і мінімального значень елементів рядків матриці А; yi – різниця максимального і мінімального значень елементів рядків матриці В.
Пошук мінімальних та максимальних значень елементів рядків оформити у вигляді підпрограми.
№2
Задано дві матриці А та В розмірності n n (n = 5). Обчислити y c k2 d l2 ,
де c = 0,5; d = 4,89;
k – кількість додатних елементів матриці А, що лежать нижче головної діагоналі; l – кількість додатних елементів матриці B, що лежать нижче головної діагоналі; Обчислення кількості додатних елементів оформити у вигляді підпрограми.
№3
Задано дві матриці A3х3 та B4х4. Розв’язати рівняння
amin x = bmin,
де amin – мінімальний елемент матриці A; bmin – мінімальний елемент матриці B.
Обчислення мінімального елемента оформити у вигляді підпрограми.
№4
Задано дві матриці A3х3 та B4х4..Знайти мінімальні елементи в матрицях А та В. Записати нулі в матриці на ті місця, де вони знаходяться.
Пошук мінімального елемента матриці оформити у вигляді підпрограми.
№5
Задано дві матриці А та В розмірності n n (n = 5). Обчислити скалярний добуток векторів x та y, де
x – вектор, компонентами якого є максимальні елементи рядків матриці A; y – вектор, компонентами якого є максимальні елементи рядків матриці B.
Формування компонент вектора із максимальних елементів рядків матриці оформити у вигляді підпрограми.
№6
Задано дві матриці А та В розмірності n n (n = 3). Розв’язати рівняння c x = d,
де c – сума додатних елементів матриці A; d – сума додатних елементів матриці B.
Обчислення сумидодатнихелементівматриціоформити у виглядіпідпрограми.
172

№7
Задано дві матриці А та В розмірності n n (n = 4). Обчислити p arctg c ln d 4,5 ,
дес–довжинавектораx,компонентамиякогоємінімальніелементирядківматриціA; d–довжинавектораy,компонентамиякогоємінімальніелементирядківматриціB.
Формування компонент вектора із мінімальних елементів рядків матриці та знаходження довжини вектора оформити у вигляді підпрограми.
№8
Задано три матриці A3х3, D2х2, С3х3. Знайти мінімальне значення компонент вектора b bi , i 1,3 , який складається із компонентів:
b1– сума елементів головної діагоналі матриці A; b2 – сума елементів головної діагоналі матриці D; b3 – сума елементів головної діагоналі матриці C;
Обчисленнясумиелементівголовноїдіагоналіматриціоформитиувиглядіпідпрограми.
№9
Задано дві матриці А та В розмірності n n (n = 3). Обчислити f 
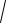 c2 d2 ,
c2 d2 ,
де с – середнє арифметичне вектора x, компонентами якого є добутки елементів стовпців матриці A;
d – середнє арифметичне вектора y, компонентами якого є добутки елементів стовпців матриці B.
Формування компонент вектора із добутків стовпців матриці та знаходження середнього арифметичного оформити у вигляді підпрограми.
№10
Задані дві матриці А3х3 та В4х4. Побудувати таблицю значень функції y=cx2 + d,
де x = {0; 0,1; …; 1};
c- сума діагональних елементів матриці A; d- сума діагональних елементів матриці B;
Обчисленнясумидіагональнихелементівматриціоформитиувиглядіпідпрограми.
№11
Задано дві матриці А та В розмірності n n (n = 5). Обчислити p sin2c 3
 c2 d2 ,
c2 d2 ,
де с – середнє геометричне компонент вектора x, якими суми модулів елементів рядків матриці A;
d – середнє геометричне компонентів вектора y, якими є суми модулів елементів рядків матриці B.
Формування компонент вектора із суми модулів елементів рядків матриці та знаходження середнього геометричного оформити у вигляді підпрограми.
173

№12
Задано дві матриці А та В розмірності n n (n = 3). Розв’язати рівняння
sA x = sB,
де sA – сума елементів матриці А; sB – сума елементів матриці В.
Обчислення суми елементів матриці оформити у вигляді підпрограми.
№13
Задано три матриці A2x2, B2х2 та C3х3. Розв’язати рівняння px2 + qx + r = 0,
де р – мінімальний елемент матриці A;
q– мінімальний елемент матриці B;
r– мінімальний елемент матриці C.
Пошук мінімального елемента матриці оформити у вигляді підпрограми.
№14
Задано дві матриці А та В розмірності n n (n = 3). Обчислити компоненти вектора z = x + y, де
x – вектор, компонентами якого є добутки елементів рядків матриці A; y – вектор, компонентами якого є добутки елементів рядків матриці B.
Формування компонент вектора із добутків елементів рядків матриці оформити у вигляді підпрограми.
№15
Задано дві матриці А3х3 та В4х4. Побудувати таблицю значень функції y=cx2 + d,
де x = { 0; 0,1;…; 1};
с – слід матриці А; d – слід матриці В.
Обчислення сліду матриці оформити у вигляді підпрограми (слідом матриці називається сума елементів головної діагоналі).
№16
Задано дві матриці А та В розмірності n n (n = 4).Обчислити f ln c ,
де с – скалярний добуток векторів x та y;
x – вектор, компонентами якого є мінімальні елементи стовпців матриці A; y – вектор, компонентами якого є мінімальні елементи стовпців матриці B. Формування компонент вектора із мінімальних елементів стовпців матриці
оформити у вигляді підпрограми.
174

№17
Задано дві матриці А та В розмірності n n (n = 5). Обчислити
w arctgc sin2 d ,
де с – сума компонент вектора x, якими є добутки додатних елементів стовпців матриці A;
d – сума компонент вектора y, якими є добутки додатних елементів стовпців матриці B.
Формування компонент вектора із добутків додатних елементів стовпців матриці та знаходження суми компонент вектора оформити у вигляді підпрограми.
№18
Задано дві матриці А та В розмірності n n (n = 4). Розв’язати рівняння c x = d,
де с – добуток додатних діагональних елементів матриці А; d – добуток додатних діагональних елементів матриці B.
Обчислення добутку додатних діагональних елементів матриці оформити у вигляді підпрограми.
№19
Задано дві матриці A = {aij}; i, j = 1, 2; B = {bk,m}; k, m = 1, 3. З’ясувати та надрукувати скільки з них являються симетричними (нуль, одна, дві). Матриця називається симетричною, якщо транспонована матриця рівна початковій.
Транспонування матриці оформити у вигляді підпрограми.
№20
Задано три матриці А, В, С розмірності n n (n = 6). Обчислити p 
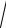 x2 y2 arctg z ,
x2 y2 arctg z ,
де x – сума максимальних елементів рядків матриці А; y – сума максимальних елементів рядків матриці В; z – сума максимальних елементів рядків матриці C;
Пошук максимальних елементів рядків та знаходження їх суми оформити у вигляді підпрограми.
№21
Задано три матриці А, В, С розмірності n n (n = 5). Обчислити
p cos(x y) tg z ,
де x – сума діагональних елементів матриці А; y – сума діагональних елементів матриці В; z – сума діагональних елементів матриці С.
Знаходження суми діагональних елементів оформити у вигляді підпрограми.
175

№22
Задано дві матриці А та B розмірності n n (n = 6). Обчислити
p arctg(x y) cos(x y) ,
де x – максимальне значення добутків стовпців матриці А; y – максимальне значення добутків стовпців матриці В.
Обчислення добутків стовпців та знаходження максимального із цих значень оформити у вигляді підпрограми.
№23
Задано дві матриці А та В розмірності n n (n = 5). Обчислити
cos y sin x ,
де x – різниця максимального і мінімального значень елементів матриці А; y – різниця максимального і мінімального значень елементів матриці В.
Пошук мінімальнихтамаксимальнихзначень оформити увиглядіпідпрограми.
№24
Задано три матриці А, В, С розмірності n n (n = 4). Обчислити
f ln x y cos x z ,
де x – максимальне значення серед мінімальних елементів стовпців матриці А; y – максимальне значення серед мінімальних елементів стовпців матриці В; z – максимальне значення серед мінімальних елементів стовпців матриці С. Пошук мінімальних елементів стовпців та максимального значення серед
них оформити у вигляді підпрограми.
№25
Задано три матриці А, В, С розмірності n n (n = 5) та число k. Обчислити p lg 
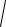 x2 y2 sin(x z) ,
x2 y2 sin(x z) ,
де x – сума діагональних елементів матриці А, більших заданого числа k; y – сума діагональних елементів матриці В, більших заданого числа k; z – сума діагональних елементів матриці С, більших заданого числа k.
Знаходження суми діагональних елементів оформити у вигляді підпрограми.
№26
Задано три матриці А, В, С розмірності n n (n = 6). Обчислити f ln x y tg x z ,
де x – максимальне значення серед сум елементів стовпців матриці А; y – максимальне значення серед сум елементів стовпців матриці В; z – максимальне значення серед сум елементів стовпців матриці С.
Обчислення сум елементів стовпців та максимального значення серед них оформити у вигляді підпрограми.
176

№27
Задано три матриці А, В, С розмірності n n (n = 4). Обчислити
p cos x ey sin z , cos y sin z
де x – мінімальне значення серед максимальних елементів стовпців матриці А; y – мінімальне значення серед максимальних елементів стовпців матриці В; z – мінімальне значення серед максимальних елементів стовпців матриці С. Пошук максимальних елементів стовпців та мінімального значення серед
них оформити у вигляді підпрограми.
№28
Задано три матриці А, В, С розмірності n n (n = 4). Обчислити p arctg x ctg y cos z,
де x – мінімальне значення серед сум елементів рядків матриці А; y – мінімальне значення серед сум елементів рядків матриці В; z – мінімальне значення серед сум елементів рядків матриці С.
Обчислення сум елементів стовпців та мінімального значення серед них оформити у вигляді підпрограми.
№29
Задано дві матриці А та В розмірності n n (n = 4). Обчислити y = x2 + z2,
де x – сума елементів матриці А, розташованих нижче головної діагоналі; z – сума елементів матриці B, розташованих нижче головної діагоналі.
Обчислення суми елементів, розташованих нижче головної діагоналі, оформити у вигляді підпрограми.
№30
Задано три матриці А, В, C розмірності n n (n = 3). Обчислити d = x (z + y),
де x – сума елементів матриці А, розташованих вище головної діагоналі;
y– сума елементів матриці B, розташованих вище головної діагоналі;
z– сума елементів матриці C, розташованих вище головної діагоналі. Обчислення суми елементів, розташованих вище головної діагоналі, офор-
мити у вигляді підпрограми.
Вимоги до оформлення практичної СРС
Вимоги для оформлення аналогічні вимогам щодо СРС-4, 5 (див. 2.6.2).
177
Література
1.Михаэль Райтингер, Геральд Муч.Visual Basic 6.0/Перевод с немецкого – К.: "Ирина". – 2001. – 285с.
2.Джон Кларк Крейг, Джефф Уэбб. Visual Basic 6.0/Перевод с английского.– 5-е изд.–М.: Издательско–торговый дом “Русская Редакция”.–2001. – 720 с.
3.Литвиненко Т.В. Visual Basic 6.0: Учебное пособие для вузов. М.: Горячая линия– Телеком.– 2001. – 140с.
4.Глушаков С.В., Сурядный А.С. Программирование на Visual Basic 6.0/ Харьков: ”ФОЛИО”. – 2002. – 497с.
5.Кульменко В.Г. Visual Basic 6.0. Самоучитель/ М.: ”БИНОМ”. – 2002. –397с.
6.Н.М. Войтюшенко, Ф.І. Останець. Інформатика і комп’ютерна техніка/ Учбовий посібник. Київ. – 2006. – 563с.
Підписано до друку 18.06.2009 р. Формат 60х84/16 Папір офсетний №1. Гарнітура Times.
Вк. 7 Наклад 500. Зам. Л_09_0003
01103, м. Київ, вул. Кіквідзе, 39 Редакційно-видавничий відділ НТУ, тел.: 284-26-26
178

179
