Змістовий модуль 7. Гіпотеза компактності

Як уже зазначалося, будь-який об’єкт при застосуванні дискримінантних методів розпізнавання зображається вектором ознак у деякому n-вимірному просторі, де n – кількість ознак. Таким чином, будь-якому об’єктові відповідає n –вектор X = (x_j; j = 1,…,n);

де x_j – значення j –ї ознаки.

Навчальну вибірку прийнято позначати у вигляді спеціальної матриці, яка часто називається матрицею даних:

Y=( y_ij ; i =1,…, q; j = 1, … , n+1).

де q - загальна кількість представників усіх класів, n - кількість ознак;

y_ij (j = 1, … , n) – значення j–ї ознаки для i-го об’єкта;

y_{i, n+1} - клас, до якого належить i - й об’єкт.

Всі дискримінантні методи так чи інакше спираються на гіпотезу компактності. Відповідно до цієї гіпотези класові відповідає компактна множина точок у деякому просторі ознак.

Слово «компактний» тут використовується у дещо незвичному значенні. Компактною у даному розумінні називається множина точок, для якої:

• число граничних точок мале порівняно з загальним числом точок;

• будь-які дві внутрішні точки можуть бути з’єднані плавною лінією так, щоб ця лінія проходила лише через точки цієї ж множини;

• майже будь-яка внутрішня точка має в достатньо великому околі лише точки цієї ж множини.

Ми будемо для простоти розглядати випадок двох класів, ця методологія поширюється на більш загальний випадок.

Отже, нехай ми маємо два класи: К₁ і К₂. Нехай довільний вектор X описується своїми координатами: X = (x₁, ... , x_n). Кажуть, що вирішувальна функція g(X) розділяє ці класи, якщо для всіх векторів класу К₁ g(X) > 0, а для всіх векторів класу К₂ g(X) < 0.

Побудова і використання вирішувальних функцій є основою багатьох методів розпізнавання. Насправді в робочому режимі ми, як правило, не можемо знати заздалегідь, до якого класу належить даний об’єкт (саме це і потрібно визначити). Натомість, якщо у нас є деяка вирішувальна функція, що є наближенням до справжньої розділяючої функції, ми можемо на основі її аналізу прийняти певне рішення, а саме: рішення про належність вектора x класові К₁, якщо g(X) > 0, і класові К₂, якщо g(X) < 0. Це рішення може, взагалі кажучи, бути помилковим. Таким чином, метою навчання має бути отримання справжньої розділяючої функції, якщо вона існує, або побудова деякої наближеної вирішувальної функції в іншому випадку. Саме такий зміст ми будемо надалі вкладати в поняття « розділяючої (вирішувальної) функції».

Як уже зазначалося, особливо важливим є випадок, коли вирішувальна (вирішувальна) функція є лінійною, тобто є рівнянням гіперплощини і має вигляд

g(X) = w₁x₁+ … + w_nx_n + w_n+1,

коефіцієнти w_i повинні бути визначені в процесі навчання.

Одним з найпростіших методів підбору параметрів є алгоритм персептрона. Алгоритм названий так через свій тісний зв’язок з навчанням персептронів.

Алгоритм полягає в наступному. Задається початковий вектор параметрів w(0), який уточнюється по мірі розпізнавання елементів навчальної вибірки. Правила уточнення наступні:

• якщо черговий елемент навчальної вибірки x⁽ⁱ⁾ належить К₁, а g(X)  0,

то w⁽ⁱ⁺¹⁾: = w⁽ⁱ⁾ + cx⁽ⁱ⁾; c > 0;

• якщо черговий елемент навчальної вибірки x⁽ⁱ⁾ належить К₂, а g(X)  0,

то w⁽ⁱ⁺¹⁾: = w⁽ⁱ⁾ – cx⁽ⁱ⁾; c > 0;

У випадку лінійної роздільності алгоритм збігається.

Кусково-лінійні розділяючі функції є більш складними, ніж лінійні, і побудова їх є більш складною. З іншого боку, кусково-лінійна вирішувальна функція може з достатньою мірою точності апроксимувати практично будь-яку розділяючу функцію.

Важливість належного вибору простору ознак, в якому класам відповідають компактні множини точок, ілюструють наступні приклади. На усіх малюнках представники одного класу позначені кружечками, а іншого – зірочками.

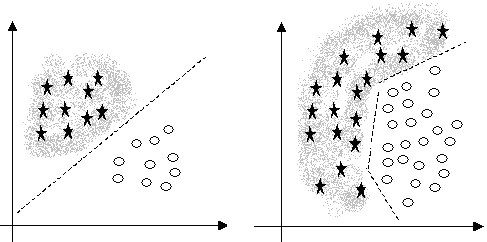
а) б)

Рис. 13. – Лінійна роздільність класів.

У даному випадку ознаки обрані дуже вдало. Класи добре відділені один від одного. Більш того, можна провести пряму лінію так, що всі представники першого класу будуть лежати по один бік цієї лінії, а всі представники другого класу – по інший бік. У такому випадку кажуть, що класи є лінійно роздільними (див. Рис. 13, а).

Лінійна роздільність дуже спрощує задачу розпізнавання. Правило розпізнавання на основі лінійних вирішувальних функцій є дуже простим і не вимагає великих затрат часу і пам’яті. Розділяючу пряму лінію дуже легко побудувати.

У прикладі (див. Рис. 13, б) лінійної роздільності немає. Але все-таки можна побудувати лінію, хоч і не пряму, яка відокремлює один клас від іншого. Процедури навчання і розпізнавання в цьому випадку суттєво ускладнюються.

В випадку (див. Рис. 14, а) надійно відокремити один клас від іншого не вдається, і це значно збільшує кількість помилок при розпізнаванні.

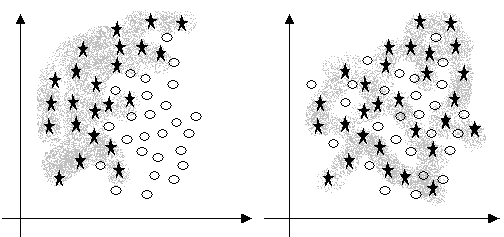
а) б)

Рис. 14. – Класи частково або повністю перекриваються

В випадку (див. Рис. 14, б) ні про яке розпізнавання в такому просторі ознак говорити, очевидно, не доводиться.

Метричні методи відносять екземпляр до того класу, відстань до центру якого менше. Таке поділ буде безпомилковим, якщо класи добре розділяються і мають сферичне угрупування навколо центрів класів.

У ситуації ж, зображеній на Рис. 15. екземпляри класів А і B згруповані навколо центрів класів, але області цих угрупувань витягнуті.

В цьому випадку екземпляр, що належить класу В (позначений «»), метрична класифікація буде помилково відносити до класу А, оскільки по відстані він ближче до А.

Рис. 15. – Окремий випадок помилкової класифікації на основі метричних методів.

Проте, легко бачити, що даний екземпляр знаходиться усередині області, межа якої може бути апроксимована за навчальними даними і цей екземпляр можна було б цілком упевнено віднести до класу В, якби класифікація здійснювалася по приналежності екземпляра до області класу (фігурі, обмеженій деякою поверхнею, що апроксимує межу області класу за точковими даними навчального експерименту).

Нехай в k-вимірному признаковому просторі є однозв'язна область з центром в точці C, обмежена поверхнею L(x), тоді точка x_q знаходитиметься на поверхні L(x), якщо L(x_q) = 0; перебуватиме усередині області з центром в точці C, якщо L(x_q) < 0; і поза областю з центром в точці C, якщо L(x_q) > 0.

Приймемо, що x_q належить області C, якщо L(x_q)0. Тоді, якщо відомі рівняння гіперплощинL^A(X) і L^B(X), апроксимуючих межі областей класів С^A і С^В, то

x_qС^A, якщо L^A(x_q) 0, L^B(x_q) > 0;

x_qС^B, якщо L^B(x_q) 0, L^A(x_q) > 0;

x_qС^A, x_qС^B, якщо (L^A(x_q) > 0 і L^B(x_q) > 0) або (L^A(x_q) < 0 і L^B(x_q) < 0) або (L^A(x_q) = 0 і L^B(x_q) = 0).

Такі правила називатимемо упевненою класифікацією, оскільки вони однозначно визначають приналежність екземпляру.

Вирази гіперповерхонь меж областей класів, як правило, невідомі. Тому їх необхідно апроксимувати на основі точкових значень ознак екземплярів навчальної вибірки, що належать відповідним класам.

Крім того, на практиці відомі на всі можливі екземпляри, що належать С^А і С^В, а лише деяка невелика підмножина таких екземплярів (навчальна вибірка). Тому L^A і L^B, побудовані на основі навчальної вибірки, обмежуватимуть не області класів для генеральної сукупності екземплярів, а області класів для екземплярів навчальної вибірки і забезпечують упевнену класифікацію лише в цих областях. Поза даними областями класифікація на основі вищеописаних правил буде неможлива (відмова від класифікації).

Якщо ввести пріоритети для класів, визначивши, що екземпляр x_q відноситься до класу А, якщо L^A(x_q) 0 і до класуВ – інакше, то це правило дозволить здійснювати класифікацію у всьому признаковому просторі, але при цьому певна частина екземплярів, які належать до класу А, але не потрапляють в область С^А (тобто не входять в навчальну вибірку) можуть бути помилково віднесені до класу В.

Вибір виразу для L^p(x), де p={A, В} позначення класу, проводиться з урахуванням попередньої інформації про характер зосередження екземплярів.

Наприклад, для L^p(x) можна використовувати рівняння гіпереліпсоїда (окремим випадком якого є гіперсфера):

,

де - деякі константи, що визначають напіврадіуси еліпсоїда. Константислід знаходити за даними навчальної вибірки, наприклад, за таким правилом:

.

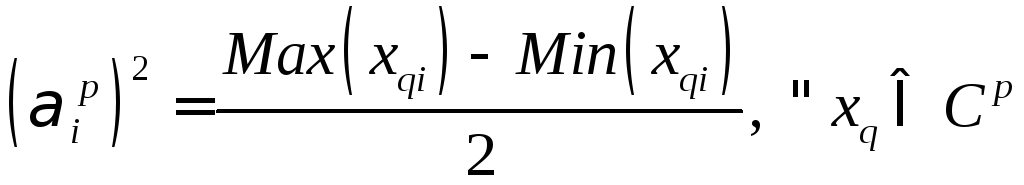Так, як центри еліпсоїдів, апроксимуючих межі областей класів, знаходяться не на початку координат, а зміщені в центри зосередження класів, то в L^p(x) необхідно врахувати цей зсув, який по i-ої координаті буде рівне i-ой координаті центру p-ої області :

.