Konspekt_lektsy_zm_1_2_3977714072-716176886

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет Городского Хозяйства им. А.Н. Бекетова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

; (v ≠ 0) ;

.pdf

Скачиваний:

Добавлен:

28.02.2016

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Логарифмічне диференціювання застосовується у двох випадках:

1) коли функція має вигляд змінної у змінному ступеню і 2) коли функція складається з трьох або більше множників у чисельнику або знаменнику.

У цих випадках спочатку логарифмуємо рівність y = f (x) , а потім візьмемо похідну від обох частин рівності і знайдемо y'.

Приклад. Знайти похідну y = xx .

Розв’язання. Логарифмуємо обидві частини ln y = ln xx = x ln x ; беремо похідну від обох частин рівності ln y = x ln x .

Маємо

y'=1 ln x + x 1 . Таким чином

= ln x +1.

Звідси y'= y(ln x +1) = xx (ln x +1).

Приклад. Знайти похідну y =

x2(x −1)3

(2x

+1)4

(x −1)3

Розв’язання. Логарифмуємо

ln y = ln

(2x +1)4

= ln x2 + ln(x −1)3 − ln(2x +1)4 =2ln x + 3ln(x −1) − 4ln(2x −1).

Беремо похідну від обох частин.

y'= 2 +

−

4 2

x −1

2x +1

(x −1)3

4 2

Звідси y'= y

−

(2x +1)4

x x −1

2x +1

x −1

2x +1

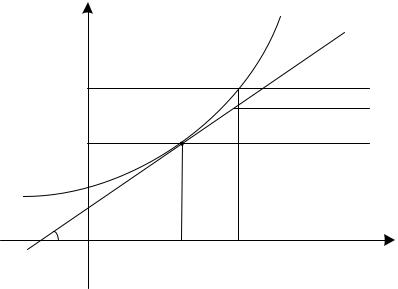
Так як з геометричної точки зору похідна дорівнює кутовому коефіцієнту дотичної функції y = f (x) , у точці x0 , то рівняння дотичної матиме вигляд y − y0 = f '(x0 )(x − x0 ) . Якщо дотична паралельна осі OY , її рівнянням буде x = x0 . Нормаль до кривої y = f (x) перпендикулярна дотичній. Враховуючи умову перпендикулярності, рівняння нормалі матиме

вигляд y − y0	= −	1	(x − x0). Якщо ж нормаль паралельна осі OX , її
		f '(x0)

рівняння буде y = y0 .

Приклад. Скласти рівняння дотичної та нормалі до кривої y = x3 − 3x2 − 2 у точці з абсцисою x0 = 1.

Розв’язання. Знайдемо ординату точки дотику y = 13 − 3 12 − 2 = −4.

Кутовий коефіцієнт дотичної k дорівнює k = y'(x0) = 3x2 − 6x = 3 − 6 = −3. Тоді рівняння дотичної матиме вигляд y + 4 = (−3)(x −1) або y = −3x −1, а


рівняння нормалі – y + 4 = −	1	(x −1) або y =		1	x −			13	.
рівняння нормалі – y + 4 = −		(x −1) або y =			x −				.
	− 3		3				3
Кут між двома кривими			y = f1(x); y = f2 (x)							у		точці		їх перетину
M (x0; y0) обчислюється як кут між дотичними до цих кривих у точці M .
Тангенс цього кута знайдемо за формулою tgϕ =							f '2 (x0) − f '1 (x0 )										.
Тангенс цього кута знайдемо за формулою tgϕ =						1										)	.
						1	+ f ' (x				0	) f '	2	(x	0	)
							1				0		2		0

Фізичний сенс похідної це швидкість руху точки у момент часу t0 , якщо точка рухається прямолінійно за законом S = S(t) , тобто v = S(t) .

Розглядаючи похідні більш високих порядків відзначимо, що похідною другого порядку або другою похідною функції y = f (x) називається похідна від її першої похідної, тобто y"= (y')'. Другу похідну позначають ще й

так yn = ∂n y = (yn−1)' .

∂xn

Якщо S = S(t) закон прямолінійного руху точки, то друга похідна від

путі по часу ∂2s є прискорення руху цієї точки.

∂t2

Якщо функція задана у параметричній формі x =ϕ(t) , y =ψ (t), то

похідні більш високих порядків обчислюються по формулам y'x = y't ; x't

(y'x )

(y"

)'t

; y'''

xxx

і так далі.

x't

Наприклад.

x't y"tt −x"tt y't

y"tt x't −x"tt y't

(x'

)2 x'

(x' )3

	5. Диференціал
Диференціалом	функції	y = f (x)	називається	головна	частина
приросту функції, лінійна відносно приросту аргумента (рис. 14).
Диференціалом	аргумента	називається приріст		аргумента	dx =	x .
Диференціал функції дорівнює добутку похідної на диференціал аргументу
dy = f '(x)dx.
у(х + х)		α (	х)
	у	α (	х)
	у
у(х)		А	х = у' dx = dy
у(х)
				х = dx
α		х
	х	х + х		х

Рис. 14

З геометричної точки зору диференціал є приріст ординати дотичної до графіка функції у точці M (x; y).

Основні властивості диференціала:

1)dc = 0, де с = const ;

2)dcu = cdu ;

3)d(u ± v) = du ± dv;

4)d(uv) = udv + vdu ;

6) df (u) = f '(u)du .

Приріст функції дорівнює диференціалу (головна частина приросту) і

величині більш високого порядку малості ніж																						x .

																y = dy + 0( x)					.

Якщо x → 0, то 0(														x)		тим паче прямує до нуля. Таким чином при,
x → 0,		y ≈ dy, або							y(x +					x) − y(x) ≈ dy = y'(x)											x .

Тоді										y(x +					x) ≈ y(x) + y'(x)						x				.

Ця формула використовується для наближених обчислень, якщо x
мале.
Приклад. Обчислити наближене значення 4																											.
Приклад. Обчислити наближене значення 4																							16,2				.
																	1
Розв’язання. 4											= (16 + 0,2)4 , де x =16,
Розв’язання. 4							16,2				= (16 + 0,2)4 , де x =16,														x = 0,2.
			1					1				1		−		3					1 '					1		3
Тоді (16 + 0,2)			4	≈ (16)				4	+															=			x	−
			4					4																				−
												4	16			4 0,2, так як x4										4		4 .
												4														4

	4		≈ 4			+				1					0,2			= 2 +		0,1						= 2 +			0,1	= 2,00625.
Звідси		16,2			16					1					0,2					0,1									0,1
Звідси		16,2			16														2 2 2 2
									4			4 16			16 16				2 2 2 2									16

Диференціалом другого порядку називається диференціал від диференціала першого порядку: d2 y = d(dy). Взагалі dn y = d(dn−1y).

Диференціали другого і вищого порядку обчислюються за формулами:

d2 y = y"(dx)2 ; d3 y = y"(dx)3 ; dn y = y"(dx)n .

Приклад. Обчислити диференціали першого, другого і третього

порядку від функції y = (ax + b)3 .
Розв’язання.	dy = 3(ax + b)2 adx ;	d 2 y = 6(ax + b) a2(dx)2 ;
d3 y = 6a a2 (dx)3 =6a3(dx)3.

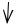
6. Основні теореми диференціального числення

Розглянемо теореми, що мають велике теоретичне й прикладне значення.

Теорема Ролля (теорема про корені похідної). Якщо функція f (x)

неперервна

на

відрізку

[a,b],

диференційована на

інтервалі (a,b) і

f (a) = f (b), то знайдеться хоча б одна точка c (a,b) в якій f '(c) = 0 .

Доведення. Так як функція

f (x)

неперервна на [a,b], то вона досягає

свого найбільшого M й найменшого значення m на цьому відрізку.

Якщо M = m , то f (x)

стала на [a,b] ,тоді f '(x) = 0 у будь-якій точці

відрізку і теорема доведена.

Якщо M ≠ m , то f (x)

досягає найбільшого або найменшого значення

у внутрішній точці, так як

f (a) = f (b).

Нехай

f (c) = M , де c (a,b): f (c) ≥ f (x).

Тоді f (c +

x) − f (c) ≤ 0 як при

x > 0 так і при

x < 0.

Отже

f (c +

x) − f (c)

≤ 0, коли

x > 0 ,

f (c +

x) − f (c)

≥ 0, коли

x < 0 .

Перейдемо до границі при

x → 0.

lim

f (c +

x) − f (c)

= f '(c) ≤ 0, коли

x > 0;

x→0

lim

f (c +

x) − f (c)

= f '(c) ≥ 0, коли

x < 0 ,

x→0

а це можливо лише тоді, коли f '(c) = 0. Геометрично це означає що дотична до графіка y = f (x) у точці c паралельна осі абсцис.

Якщо ж f (a) = f (b) = 0, то це означає, що між двома коренями функції існує хоча б один корінь похідної.

Теорема Коші. (про відношення приросту двох функцій). Якщо функції f (x) і ϕ(x) неперервні на відрізку [a,b], диференційовані на інтервалі (a,b),


причому ϕ'( x )		ніде не		обертається		у нуль, то знайдеться	така	точка
c (a,b), що	f (b) − f (a)		=	f '(c)	.
				ϕ'(c)
	ϕ(b) − ϕ(a)
Доведення.		Зауважимо,			що	f (b) − f (a) ≠ 0 , так	як	якщо

f (b )− f ( a ) = 0 , то за теоремою Ролля знайдеться така точка c , де ϕ'(c) = 0, а це не так, за умовою теореми.

Визначимо число Q рівністю	f (b) − f (a)	, складемо допоміжну
	ϕ(b) −ϕ(a)

функцію F(x) = f (x) − f (a) − Q[ϕ(x) −ϕ(a)]. Ця функція задовольняє умовам теореми Ролля: неперервна і диференційована на [a,b], F(b) = F(a) = 0 . Тоді

знайдеться		хоча		б одна	точка x = c (a,b), така, що F'(c) = 0 .		Але
	F'(x) = f '(x) − Qϕ'(x), отже				F'(c) = f '(c) − Qϕ'(c) = 0, звідси Q =	f '(c)	. Тоді
	F'(x) = f '(x) − Qϕ'(x), отже				F'(c) = f '(c) − Qϕ'(c) = 0, звідси Q =	ϕ'(c)	. Тоді
						ϕ'(c)
	f (a) − f (b)	=	f '(c)	, що й треба було довести.


	ϕ(a) −ϕ(b)		ϕ'(c)
	ϕ(a) −ϕ(b)		ϕ'(c)

Теорема Лагранжа (про скінченні прирости функції). Якщо функція f (x) неперервна і диференційована на відрізку [a,b], то знайдеться хоча б одна точка c (a,b), така що f (b) − f (a) = f '(c)(b − a).

Доведення. Теорема Лагранжа є частковим випадком теореми Коші.

Дійсно, поклавши ϕ(x)

ϕ'( c ) = 1. Тоді з формули

що й треба було довести.

= x, знаходимо			ϕ(b)	−ϕ(a) = b − a , ϕ'(x) = 1,
f (b) − f (a)	=	f '(c)	, або	f (b) − f (a) = f '(c)(b − a),
ϕ(b) − ϕ(a)	=	ϕ'(c)	, або	f (b) − f (a) = f '(c)(b − a),
ϕ(b) − ϕ(a)		ϕ'(c)

Геометрично це означає, що на дузі графіка функції y = f (x) знайдеться точка C між A і B , у якій дотична паралельна хорді, яка з’єднує точки A і B (рис. 15).

y
		C	y=f(x)
		C	B
α		A
α	α
	α
0	a	c	b

Рис. 15

Правило Лопіталя розкриття невизначеностей.

Теорема. Нехай функції f (x) і ϕ(x) диференційовані у ε -околі точки x0 і

ϕ'(x) ≠ 0.

Якщо

lim f (x) =

lim

ϕ (x) = 0 ,

або

lim f (x) = lim ϕ (x) = ∞ ,

тобто

x→x0

частка

точці

x = x0

представляє

собою

невизначеність

виду

, або

∞

, то lim

f (x)

f '(x)

, при умові, що існує границя відношення

∞

x→x0

ϕ(x)

ϕ'(x)

похідних. Доведення спирається на доведення теореми Коші при умові, що

x ≠ a, x (a, x) і	f (a) = ϕ(a) = 0 . Тоді				f (x)		=	f '(x0 )	.
x ≠ a, x (a, x) і	f (a) = ϕ(a) = 0 . Тоді						=		.
0				ϕ(x)				ϕ'(x0 )
				ϕ(x)				ϕ'(x0 )
Якщо частка		f '(x0 )	у точці x = x			також є невизначеність виду				0	або
Якщо частка			у точці x = x			також є невизначеність виду					або
		ϕ'(x0 )		0			0
		ϕ'(x0 )					0

∞∞ і похідні f '(x) і ϕ'(x) задовольняють відповідним умовам, то переходимо до відношення других похідних і так далі.

У випадку

невизначеностей

виду

0 ∞ або ∞ ∞ треба провести

алгебраїчні перетворення.

Наприклад.

0 ∞ =

або

0 ∞ =

∞

∞ .

∞

У випадку невизначеностей виду 00 , ∞0 , 1∞ треба прологарифмувати дану функцію і знайти границю її логарифма, або скористатися наступною таблицею:

a) ∞0 = eln ∞0 = e0 ln ∞ = e0 ∞ = e1/ ∞ = e0 ;

b) 00 = eln 00 = e0 ln 0 = e0 ∞ = e1/ ∞ = e0 ;

c)1∞ = eln1∞ = e∞ ln1 = e∞ 0 = e1/ ∞ = e0 .

Розглянемо приклади.

sin x

x − tgx

1−

−2

= −

1 .

Приклад. lim

= lim

cos2 x

= lim

cos3 x

x→0

2x3

x→0

6x2

x→0

12x

Приклад.

ln(x − а)

∞

ex − eа

lim

= lim

x − а

= e−а lim

eх

=1.

∞

x→а ln(ex − eа )

x→а

x→а x − а

x→а

ex − eа

Приклад

∞ − ∞

1 −1

−1

ln x − x +1

lim

−

= lim

= −

(x −

1)ln x

ln x

x→1

x −1

x→1

ln x + (x −1)

x→1 1

Приклад.

lim

ln x

lim

−cos x

limsin xln x

x→0

lim xsin x =

= e

sin x = e

sin2 x = e0

=1.

= ex→0

x→0

(−sin 2x) 2

1∞

lim

lncos2x

3lim

cos2x

Приклад. lim(cos2x)x2 =

= ex→0 x2

= e x→0

sin2x

x→0

~ 2x

−3lim2x

cos2x → 1

= e

x→0 x = e−6.

x→0

7. Застосування похідної

Умови монотонності функції. Екстремуми

Функція f (x) називається зростаючою у точці x0 , якщо при достатньо малому h > 0 виконуються умови

f (x0 − h) < f (x0 ) < f (x0 + h) .

Функція f (x) називається спадаючою у точці x0 , якщо при достатньо малому h > 0 виконуються умови

f (x0 − h) > f (x0 ) > f (x0 + h).

Функція f (x) називається зростаючою на інтервалі (a,b), якщо для будь яких двох точок x1 та x2 , що належать (a,b) , за умови x1 < x2 , виконується нерівність f (x1) < f (x2 ) .

Функція f (x) називається спадаючою на інтервалі (a,b) , якщо для будь яких двох точок x1 та x2 , що належать (a,b), за умови x1 < x2 , виконується нерівність f (x1) > f (x2 ).

Ознаки зростання та спаду функцій

1)Якщо f '(x0 ) > 0, то функція f ( x ) зростає у точці x0 .

2)Якщо f '(x0 ) < 0, то функція f ( x ) спадає у точці x0 .

Значення f (x0 ) називається максимумом функції f (x) , якщо при достатньо малому h > 0 виконуються умови

f (x0 − h) < f (x0 ) та f (x0 + h) < f (x0 ).

Точка x0 , у цьому випадку, має назву точки максимуму функції.

Значення f (x0 ) називається мінімумом функції f (x) , якщо при достатньо малому h > 0 виконуються умови

f (x0 − h) > f (x0 ) та f (x0 + h) > f (x0 ).

Точка x0 , у цьому випадку, має назву точки мінімуму функції.

Максимум і мінімум функції називаються екстремумами функції, а точка максимуму або мінімуму – точкою її екстремуму.

Необхідна умова існування екстремума

Теорема. Якщо диференційована функція y = f (x) має у точці x0 екстремум, то, її похідна у цій точці дорівнює нулю, тобто f '(x0 ) = 0, або не існує.

Доведення цієї теореми спирається на теорему Ролля.

Точка x0 у якій f '(x0 ) = 0 має назву стаціонарної точки.

Точки у яких f '(x) = 0 або f '(x) не існує мають назву критичних точок першого роду. Не кожна критична точка є точкою екстремуму. Розглянемо достатні умови екстремуму.

Перша умова.

Теорема. Якщо неперервна функція y = f (x) диференційована у

ε -околі критичної точки x0 (крім, може бути, самої цієї точки) при переході через цю точку зліва направо f '(x) змінює знак з плюса на мінус, то функція f (x) у точці x0 має максимум, а якщо з мінуса на плюс, то функція f (x) у

точці x0 має мінімум.

Доведення. Розглянемо ε -окіл точки x0 . Нехай виконуються умови:


f '(x) > 0,		x (x0 − ε, x0 ) і f '(x) < 0, x (x0 , x0 + ε ).			Тоді функція f (x)
зростає на		інтервалі	(x0 − ε; x0 )	і спадає на інтервалі	(x0 , x0 + ε ) . Отже
значення функції f (x)			у точці x0	є найбільшим на інтервалі (x0 − ε, x0 + ε ) ,
тобто	f (x) < f (x0 ) для усіх x (x0 − ε, x0 ) U (x0 , x0 + ε ), а це й означає, що
точка	x0 – точка максимуму функції.

Графічно інтерпретація доведення теореми представлена на рис. 16.

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.02.2016792.06 Кб71KL_EA_2004.doc
#
28.02.2016228.45 Кб6Kobylyakova.docx
#
27.02.2016821.76 Кб130Konspekt_lektsiy_OP_v_galuzi_EO_ES_MA.doc
#
27.02.20161.6 Mб73konspekt_lektsyy_el_aparati3.doc
#
27.02.2016709.12 Кб53Konspekt_lektsy_TBO.doc
#
28.02.20161.39 Mб6Konspekt_lektsy_zm_1_2_3977714072-716176886.pdf
#
28.02.2016876.74 Кб22Konspekt_mikroprotsesorna_tekhnika.pdf
#
27.02.201615.06 Mб169Kopia_KL_Prikl_gidroekologia_modul1-4.doc
#
27.02.20161.85 Mб22KP.doc
#
27.02.2016514.56 Кб182KR_OGG_2_semestr2013.doc
#
27.02.2016154.11 Кб14kursovaya_3.doc