
Konspekt_lektsy_zm_1_2_3977714072-716176886
.pdf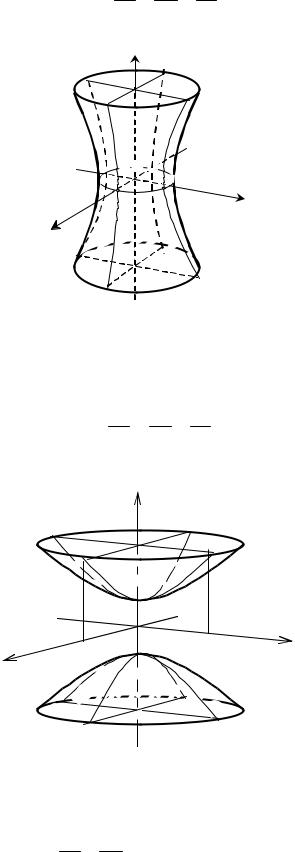
x2 y2 z2
однопорожнинний гіперболоїд a2 + b2 − c2 =1 (рис. 31);
z
c
a |
b |
y |
|
|
|
x |
|
|
Рис. 31
x2 y2 z2
двопорожнинний гіперболоїд a2 + b2 − c2 = −1 (рис. 32);
z
2c
|
c |
|
a |
b |
y |
|
|
x
Рис. 32
еліптичний параболоїд x2 + y2 = 2z ( p > 0, q > 0) (рис. 33);
pq
101
z
y
x
Рис. 33
гіперболічний параболоїд x2 − y2 = 2z ( p > 0, q > 0) (рис. 34).
pq
z
x
y
Рис. 34
Таким чином, існує дев’ять поверхонь другого порядку: три циліндри – еліптичний, гіперболічний та параболічний, конус, еліпсоїд, однопорожнинний гіперболоїд, двопорожнинний гіперболоїд, еліптичний параболоїд, еліптичний параболоїд та гіперболічний параболоїд.
Слід зауважити, що загальне рівняння поверхонь другого порядку може також визначати сукупність двох площин, точку, пряму і, навіть, не мати геометричного змісту (визначати уявну поверхню).
102
Приклад. З’ясувати геометричний сенс рівняння
x2 + 4y2 + 9z2 +12yz + 6xz + 4xy − 4x − 8y −12z + 3 = 0
Розв’язання. Здійснюючи алгебраїчні перетворення, отримаємо
рівняння |
|
|
|
|
|
|
(x + 2y + 3z)2 − 4(x + 2y + 3z) + 3 = 0 або |
(x + 2y + 3z −1)(x + 2y + 3z − 3) = 0 . |
|||||
Таким чином, |
рівняння визначає сукупність двох |
площин |
||||
x + 2y + 3z −1= 0 та x + 2y + 3z − 3 = 0. |
|
|
|
|||
Приклад. |
Звести |
до |
канонічного |
виду |
рівняння |
|
x2 + y2 + 4z2 − 2xy − 8z + 5 = 0. |
|
|
|
|
||
Розв’язання. |
|
Згрупуємо |
члени |
наступним |
чином |
|
(x − y)2 + 4(z −1)2 = −1. |
|
|
|
|
|
|
Це рівняння не має геометричного сенсу, бо ліва частина не може бути від’ємною для будь-яких дійсних x, y,z .
Приклад. Звести до канонічного виду рівняння 4x2 + 9y2 + 36z2 − 8x −18y − 72z +13 = 0 .
Розв’язання. Виділимо повні квадрати:
4(x2 − 2x +1−1) + 9(y2 − 2y +1−1) + 36(z2 − 2z +1−1) +13 = 0.
4(x −1)2 + 9(y −1)2 + 36(z −1)2 = 36 .
Поділимо обидві частини на тридцять шість.
(x −1)2 |
+ |
(y −1)2 |
+ |
(z −1)2 |
=1 або |
(x −1)2 |
+ |
(y −1)2 |
+ |
(z −1)2 |
=1 |
|
9 |
4 |
1 |
32 |
22 |
12 |
|||||||
|
|
|
|
|
|
це рівняння еліпсоїда, піввісі якого дорівнюють: a = 3; b = 2; c =1, а центр знаходиться у точці O(1;1;1) .
Приклад. З’ясувати, яку поверхню визначає рівняння x2 = yz .
Розв’язання. Треба перейти до нових координат, а саме: зробити поворот на кут, що дорівнює 45°, від вісі Oy до вісі Oz проти годинникової
103

стрілки. Тоді |
|
x = x′; y = y′cos45° − z′sin 45°; |
z = y′sin 45° + z′cos45° , |
або |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x = x′; |
y = |
|
|
2 |
(y′ − z′) ; |
z = |
2 |
|
(y′ + z′) , |
так |
як |
sin 45° = cos45° = |
2 |
. |
||||||||||||||||
2 |
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
Підставляючи |
|
ці |
вирази |
|
|
для |
|
x; y;z |
|
у |
рівняння |
x2 = yz отримаємо: |
||||||||||||||||||
|
2 |
|
(y′)2 |
|
|
(z′) |
2 |
|
2 |
|
|
(y′)2 |
|
(z′)2 |
|
|
|
|
|
|
|
|
||||||||
(x′) |
|
= |
|
|
− |
|
|
або (x′) |
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
= 0. |
|
|
|
|
|
|||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
2)2 |
|
2)2 |
|
|
|
|
|
|
|
|
|||||||
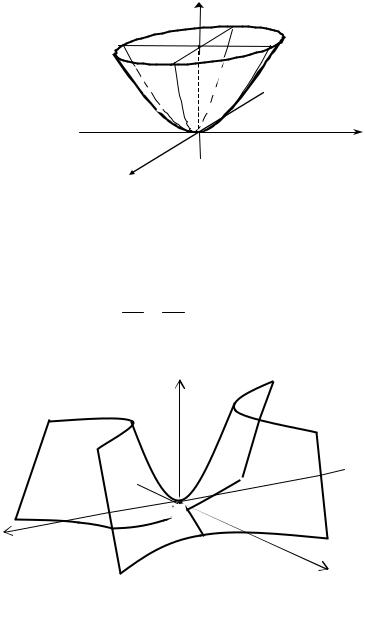
Це рівняння конусу другого порядку, віссю якого є вісь Oy′ у нових координатах.
104
Список використаних джерел
1.Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М. Наука. 1973. – 720 с.
2.Данко П.Е., Попов А.Г., Кожевникова, Высшая математика в упражнениях и задачах ч. I – М. Высш. школа, 1980. – 320 с.
3.Берман Г.Н. Сборник задач по курсу математического анализа. – М. Наука. 1985. – 384 с.
4.Станишевский С.О. Вища математика. – Харків. ХНАМГ, 2005, – 270 с.
5.Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. – М.: Физматгиз, 1966. – 366 с.
6.Дубовик В. П., Юрик І. І. Вища математика. – Київ: «Видавництво А.С.К.», 2003. – 648 с.
7.Печеніжський Ю.Є., Станішевський С.О., Тихонович О.Ю.
Посібник для розв’язування задач з вищої математики. – Х.: ХНАМГ, 2003. – 125 с.
105

Навчальне видання
БОРАКОВСЬКИЙ Олександр Васильович
Вища математика: конспект лекцій, модуль І. (для студентів 1-го курсу денної і заочної форм навчання за напрямами підготовки 6.040106 – «Екологія, охорона навколишнього середовища та збалансоване природокористування (ЕОНС)»)
Редактор М. З. Аляб’єв
План 2009, поз. 66 Л
Підп. до друку 24.12.2009 |
Формат 60х84 1/16 |
Друк на ризографі. |
Ум. друк. арк. 4,4 |
Зам. № |
Тираж 50 пр. |
Видавець і виготовлювач:
Харківська національна академія міського господарства, вул. Революції, 12, Харків, 61002
Електронна адреса: rectorat@ksame.kharkov.ua Свідоцтво суб’єкта видавничої справи: ДК №731 від 19.12.2001
106
