4. Примеры решения задач

Пример 1. Электрическое поле создано бесконечной плоскостью, заряженной с поверхностной плотностью заряда =400 нКл/м, и бесконечной прямой нитью, заряженной с линейной плотностью =100 нКл/м. Определить напряженность электрического поля в точке, находящейся на расстоянии 10 см от нити, если эта точка и нить лежат в плоскости, параллельной заряженной плоскости.

Решение

Согласно принципу суперпозиции вектор напряженности электрического поля равен векторной сумме напряженностей полей и , создаваемых соответственно плоскостью и нитью в данной точке: . (1)

Поле, создаваемое бесконечной заряженной плоскостью, однородно. Вектор его напряженности в любой точке окружаю-

щего пространства направлен нормально по отношению к плоскости. Модуль этого вектора равен:

, (2)

где - электрическая постоянная.

Поле, создаваемое бесконечной заряженной нитью, неоднородно. Вектор напряженности электрического поля нити направлен радиально от нити. Его модуль в точке на расстоянии r от нити определяется выражением:

. (3)

Как видно из рисунка, векторы и взаимно перпендикулярны, следовательно: .

Подставим выражения (2), (3) в эту формулу и проведем вычисления:

.

Вектор направлен под углом к заряженной плоскости. Из рисунка видно, что . Используя формулы (2) и (3), получим:

.

Произведя вычисления, получим . Следовательно, .

Пример 2. Электрон, имевший скорость 60 Мм/с, влетел в пространство между пластинами плоского конденсатора, заряженного до разности потенциалов U =1000 В, по линии АВ, параллельной пластинам и проходящей на одинаковом расстоянии от них. Расстояние d между пластинами равно 2 см. Длина L₁ пластин конденсатора в направлении полета электрона равна 20 см. Определить: 1) работу электрического поля по изменению скорости электрона, прошедшего сквозь конденсатор; 2) расстояние ВС на экране Э, отстоящем от конденсатора на L₂=1 м.

Решение

1. В соответствии с законом сохранения механической энергии искомая работа поля а будет равна разности кинетических энергий электрона на выходе из конденсатора (Ек) и на входе в него (е0) :

. (1)

Скорость электрона при вылете из конденсатора в точке М можно представить в виде двух составляющих: вертикальной - и горизонтальной - (см. рисунок.). Тогда:

.

Между пластинами конденсатора электрон движется равноускоренно под действием постоянной силы электростатического поля конденсатора, направленной вертикально вниз (силой тяжести, действующей на электрон, можно пренебречь ввиду ее малой величины). Следовательно,

По второму закону Ньютона ,

где - сила, с которой электрическое поле напряженностью Е действует на электрон, е – модуль заряда электрона, m - его масса.

Напряженность поля между пластинами плоского конденсатора связана с разностью потенциалов U между ними соотношением: , где d - расстояние между пластинами. Тогда ускорение . (2)

Время полета электрона внутри конденсатора найдем из формулы пути равномерного движения , откуда

, (3)

где - длина конденсатора в направлении полета электрона.

Используя выражения для (2) и (3), получим:

. (4)

Подстановка данных и расчет дают: м/с, м/с.

Тогда по формуле (1) работа: Дж.

2. На выходе из конденсатора (в точке М) электрон будет иметь смещение по вертикали (см.рис.). На участке МС движение электрона прямолинейное, с постоянной скоростью . На этом участке электрон смещается по вертикали на расстояние относительно точки М.

Очевидно, что искомое расстояние: .

Пользуясь формулой длины пути равноускоренного движения, найдем

(5)

где а - ускорение, полученное электроном под действием поля конденсатора; t - время полета электрона внутри конденсатора.

Подставляя в формулу (5) последовательно значения a и t из соответствующих выражений, получим:

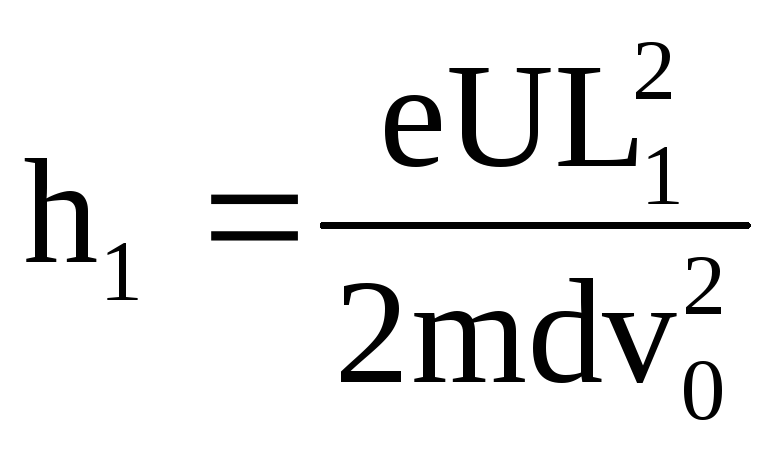. (6)

Из треугольника MDC (см. рис.) длина отрезка равна:

, (7)

где - угол между векторами скоростей и .

Из рисунка видно, что . (8)

После подстановки выражений (8) и (4) в уравнение (7), получим: .

Окончательно для искомого расстояния будем иметь:

.

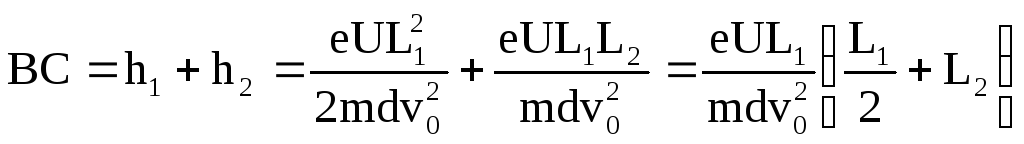Подставив значения величин в последнее выражение и произведя вычисления, получим м.

Пример 3. Конденсаторы емкостями =1 мкФ, =2 мкФ и =3 мкФ образуют цепь, показанную на рисунке. Разность потенциалов на концах цепи равна 10 В. Определить: 1) общую емкость системы; 2) разность потенциалов на каждом конденсаторе; 3) заряд каждого конденсатора; 4) энергию электрического поля каждого конденсатора и общую энергию системы.

Решение

1. Чтобы определить емкость системы, разобьем данную цепь на два участка.

Первый содержит конденса- торы и , включенные па- раллельно. Емкость этого участка:

. (1)

Последовательно к первому участку цепи подключен второй, содержащий конденсатор .

Общая емкость при последовательном включении этих участков определяется из соотношения:

,

откуда

.

Используя выражение (1), получим:

.

После подстановки численных значений найдем: С= Ф.

2. Пусть - разности потенциалов на каждом из конденсаторов, соответственно. Конденсаторы и включены параллельно, следовательно

.

Разность потенциалов на концах всей цепи:

. (2)

Первый и второй участки включены последовательно. При последовательном соединении заряд каждого участка один и тот же и равен заряду всей батареи конденсаторов. Следовательно, суммарный заряд первого участка равен заряду третьего конденсатора :

, (3)

где - заряды первого, второго и третьего конденсаторов.

Используя определение емкости конденсатора, можно записать:

; ; . (4)

Выразив из (4) и подставив в уравнение (3), получим соотношение

_,

из которого найдем: . (5)

Подставляя последнее выражение в уравнение (2), получим:

.

Отсюда . (6)

Проведя подстановку данных в выражения (5) и (6) и соответствующие расчеты, получим:5 В; = 5 В.

3. Заряды конденсаторов найдем, используя выражение (4):

; ; .

Кл; Кл; Кл.

4. Энергия электрического поля конденсатора равна:

.

После расчета с использованием соответствующих значений зарядов и емкостей, получим:

Тогда полная энергия системы равна

.

Пример 4. С каким коэффициентом полезного действия работает свинцовый аккумулятор, ЭДС которого = 2,15 В, если во внешней цепи с сопротивлением R = 0,25 Ом течет ток I=5 А? Какую максимальную полезную мощность может дать этот аккумулятор во внешней цепи? Какой КПД соответствует этой мощности?

Решение

По определению коэффициент полезного действия есть отношение полезной мощности, выделяемой во внешней цепи, ко всей мощности, выделяемой аккумулятором:

.

После подстановки численных значений получим: .

Известно, что полезная мощность электрической цепи (мощность, выделяемая на внешнем сопротивлении)равна:

. (1)

Воспользовавшись законом Ома для замкнутой цепи

, (2)

получим: . (3)

Из формулы (3) очевидно, что величина мощности Р, выделяемой во внешней цепи, зависит от величины внешнего сопротивления цепи (R). Чтобы найти экстремум функции (3) возьмем первую производную от этого выражения по R, приравняем ее нулю.

.

Проведя преобразования, получим: R = r.

Следовательно, во внешней цепи выделяется максимальная мощность, если ее сопротивление равно внутреннему сопротивлению источника тока.

Из закона Ома (2) определим внутреннее сопротивление источника тока

Ом.

Подставив в (3) значение R = r и проведя вычисления, получим:

Вт.

При этом коэффициент полезного действия

.

Пример 5. Источники тока с = 10 В и = 4 В включены в цепь, как показано на рисунке. Определить силы токов, текущих в сопротивлениях и , если == 2 Ом и == 4 Ом. Сопротивлениями источников тока пренебречь.

Решение

Силы токов в разветвленной цепи можно определить с помощью правил Кирхгофа.

Выберем направления токов, как показано на рисунке.

По первому правилу Кирхгофа для узла В имеем:

(1)

По второму правилу Кирхгофа имеем для контуров , , , соответственно:

, (2)

, (3)

. (4)

Подставив в равенства (2) - (4) значения сопротивлений и ЭДС и объединив с (1), получим систему уравнений:

Поскольку нужно найти только два тока, то для решения этой системы линейных уравнений удобно воспользоваться методом Крамера. Запишем полученную систему уравнений в виде:

Искомые значения токов найдем из выражений:

, (5)

где

Расчеты дают следующие значения определителей:

; ; .

Отсюда, по формулам (5), получаем: .

Знак минус у значения силы тока свидетельствует о том, что при первоначальном выборе направлений токов, указанных на рисунке, направление тока было выбрано противоположно истинному.

Пример 6. Два параллельных бесконечно длинных тонких проводника, по которым текут в одном направлении токи I=60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию в точке, отстоящей от одного проводника на расстояние , а от другого - на .

Решение

Для нахождения магнитной индукции в указанной точке А определим по правилу правого винта направления векторов индукций и полей, создаваемых каждым проводником в отдельности (см.рисунок). По принципу суперпозиции:

.

Модуль результирующего вектора найдем по теореме косинусов:

. (1)

Значения индукций и рассчитаем по формулам для индукции магнитного поля, создаваемого бесконечным прямым проводником с током:

, ,

где Гн/м – магнитная постоянная.

Подставляя эти выражения в (1) и вынося общий множитель за знак корня, получим:

. (2)

Из треугольника DAC несложно найти . По теореме косинусов, в наших обозначениях,

.

Отсюда: .

Подставляя данные, получим .

Подставив в формулу (2) значения всех входящих в нее величин, найдем искомую величину: В = Тл.

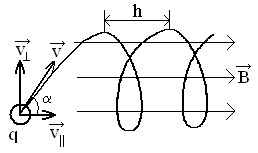
Пример 7. Электрон, имея скорость v = 2 , влетел в однородное магнитное поле с индукцией В = 30 мТл под углом к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.

Решение

Известно, что на заряженную частицу, движущуюся в однородном магнитном поле, действует сила Лоренца:

.

Модуль этой силы: где q - заряд частицы, - угол между направлением скорости и вектором магнитной индукции.

Вектор скорости электрона, влетевшего под углом в магнитное поле, можно представить в виде двух составляющих (см. рис.): , где - составляющая скорости, параллельная линиям индукции магнитного поля, - составляющая скорости, перпендикулярная индукции магнитного поля. Очевидно, что сила Лоренца, действуя в направлении, перпендикулярном скорости частицы, изменяет только направление , сообщая электрону нормальное ускорение .

По второму закону Ньютона .

Тогда .

Отсюда найдем радиус R винтовой линии, по которой будет двигаться электрон.

или .

Подставив значения величин m, v, e, B, и произведя вычисления, получим:

м.

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью за время Т, которое понадобится электрону для того, чтобы совершить один оборот: где - период вращения электрона.

Подставив выражения для Т, и в формулу для шага h, получим:

.

Используя значения величин R , и произведя вычисления, получим:

.

Пример 8. Плоский прямоугольный контур (рамка) со сторонами а = 10 см и b = 15 см, по которому течет ток силой I=100 А, свободно установился в однородном магнитном поле (В=1 Тл). Определить:1) работу , совершаемую внешними силами при повороте контура на угол относительно оси, проходящей через середины его больших сторон; 2) среднюю ЭДС, возникающую при этом, если поворот совершается за две секунды. Считать, что при повороте контура сила тока в нем поддерживается неизменной.

Решение

При перемещении контура с током в магнитном поле, поле совершает работу:

,

где Ф₁ - магнитный поток, пронизывающий контур до перемещения; Ф₂ - то же, после перемещения, I - сила тока в контуре. Из закона сохранения энергии следует, что работа внешних сил

.

По определению магнитный поток: , где S – площадь контура, - угол между вектором индукции и магнитным моментом контура (см.рис.).

По условию задачи в начальном положении контур свободно установился в магнитном поле. Такое положение контура возможно, если векторы и совпадают по направлению.

Тогда .

В конечном состоянии (после поворота на угол ) магнитный поток, пронизывающий контур:

.

Следовательно:

(Дж).

Среднее значение ЭДС найдем по закону Фарадея-Максвелла:

.

Подстановка данных приводит к результату: .

Пример 9. Толстая стеклянная пластинка покрыта тонкой пленкой и находится в воздухе. На нее падает нормально параллельный пучок монохроматического света с длиной волны 0,6 мкм. Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину пленки, если показатель преломления стекла равен 1,5, а пленки – 1,4.

Решение

Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения , показан на рисунке. В точках А и В пучок частично отражается и частично преломляется. Отраженные лучи света падают на собирающую линзу, пересекаются в ее фокусе и интерферируют между собой.

Так как показатель преломления воздуха () меньше показателя преломления вещества пленки (), который, в свою очередь, меньше показателя преломления стекла (), то в точках А и В отражение происходит от среды, оптически более плотной, чем среда, в которой идет падающая волна. При этом фаза колебаний обоих интерферирующих лучей при отражении изменяется на радиан, что приводит к уменьшению оптической длины пути каждого из пучков на . Следовательно, результат интерференции этих лучей будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого луча не было.

Как видно из рисунка, оптическая разность хода интерферирующих лучей равна:

. (1)

В результате интерференции лучи будут ослаблены, если выполняется условие минимума интенсивности:

, (2)

где k = 0, 1, 2 . . .

При угле падения , , . Приравняв правые части уравнений (1) и (2), получим:

.

Отсюда искомая толщина пленки

.

Полагая k=0, 1, 2, . . ., получим ряд возможных значений толщины пленки:

м; м и т.д.

Пример 10. На диафрагму с круглым отверстием радиусом 1 мм падает нормально параллельный пучок света с длиной волны =0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.

Решение

При дифракции Френеля на круглом отверстии в центре дифракционной картины будет наблюдаться темное пятно, если в размер отверстия укладывается четное число зон Френеля.

Следовательно, разбив отверстие диафрагмы на зоны Френеля, расстояние АО от края отверстия до точки наблюдения (см. рисунок) можно записать в виде:

АО = ,

где k = 2, 4, 6 . . .- число зон Френеля, укладывающихся в размер отверстия.

Тогда по теореме Пифагора:

.

Так как , то слагаемым, содержащим , можно пренебречь. Последнее равенство при этом перепишется в виде: .

Отсюда , где k = 2, 4, 6 . . .

Очевидно, что максимальное значение b получится при k = 2:

.

Произведя вычисления по последней формуле, найдем = 1 м.

Пример 11. На щель шириной 0,1 мм нормально падает параллельный пучок света от монохроматического источника ( = 0,6 мкм). Определить ширину центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L=1 м.

Решение

Центральный дифракционный максимум интенсивности света занимает область между ближайшими от него минимумами интенсивности. Поэтому ширину центрального максимума примем равной расстоянию между этими двумя минимумами (см. рис.).

Минимумы интенсивности света при дифракции на одной щели наблюдаются под углами , определяемыми условием:

, (1)

где k - порядок минимума. В нашем случае k равен единице.

Как видно из рисунка, . Отсюда расстояние между двумя минимумами на экране: .

Так как при малых углах , то

. (2)

Выражая из формулы (1) и подставляя в (2), получим расчетную формулу:

.

Произведя вычисления для k=1, получим м.

Пример 12. На дифракционную решетку нормально к ее поверхности падает параллельный пучок света с длиной волны =0,5 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L=1 м. Расстояние между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20, 2 см. Определить: 1) постоянную дифракционной решетки; 2) общее число максимумов, которое дает дифракционная решетка; 3) максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму.