Эконометрика / 11

 

1.     Классы нелинейных регрессий.

2.     Параболическая форма зависимости.

3.     Гиперболическая форма зависимости.

4.     Экспоненциальная форма зависимости.

5.     Степенная форма зависимости.

 

Между экономическими явлениями существуют нелиней­ные соотношения, которые выражаются с помощью нелинейных функций.

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам Примерами таких регрессий являются функции:

—полиномы разных степеней;

—равносторонняя гипербола.

2. К нелинейным регрессиям по оцениваемым параметрам от­носятся функции:

—степенная;

—показательная;

—экспоненциальная.

 

Нелинейная регрессия по включенным переменным определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), так как эти функции линейны по параметрам.

1.     Параболическая форма зависимости.

Уравнение регрессии параболы 2-го порядка имеет следующий вид:

         Нормальные уравнения метода наименьших квадратов для параболической зависимости таковы:

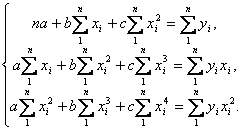
         Решая эту систему уравнений, получаем значения параметров a, b и c.

Парабола второй степени при b > 0 и с < 0 симметрична относительно точки максимума, изменяю­щей направление связи, а именно рост на падение. Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста, с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника.

При b < 0 и с > 0 парабола второго порядка симметрична относительно минимума функции в точке, меняющей направление связи, а именно  снижение на рост.

 

     2. Гиперболическая форма зависимости.

Уравнение регрессии гиперболы имеет следующий вид:

Из системы нормальных уравнений метода наименьших квадратов для гиперболы:

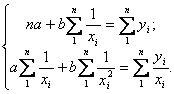
определяются значения коэффициентов гиперболического уравнения регрессии a и b.

Гиперболическая зависимость может быть использована на микро- и макроуровне - например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая соотношение между нормой безработицы и процентомприроста заработной платы.

 

Рассмотрим регрессию, нелинейную по оцениваемым пара­метрам

3.Экспоненциальная форма зависимости.

Общий вид экспоненциального уравнения регрессии:

 или .

Для упрощения алгоритма обработки выборочной совокупности проводится линеаризация экспоненциального уравнения регрессии путем логарифмирования второго из представленных  уравнений

.

 Проведя замену ln y на z, получается линейное уравнение вида:

z=a+bx.

Далее используя систему нормальных уравнений для линейной зависимости

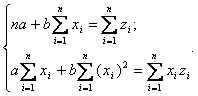
определяем параметры уравнения регрессии  a и b. Производя обратную замену,  получаем эмпирические значения результирующего признака.

4. Степенная форма зависимости.

Общий вид степенного уравнения регрессии:

.

Логарифмирование дан­ного уравнения приводит его к линейному виду:

Оценки параметров a и b уравнения могут быть найдены МНК. Система нормальных уравнений имеет вид:

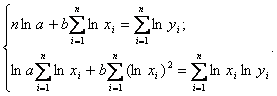
Параметр b определяется из системы, а параметр a – потенцированием выражения lna.

Показателем тесноты нелинейной корреляции является индекс корреляции, вычисляемый по формуле:

,                                                    

где - индивидуальные значения у  по уравнению связи.

Индекс корреляции находится в границах: 0 < R < 1 и чем ближе к единице, тем теснее связь рассматриваемых признаков, более надежно найденное уравнение регрессии.

Индекс детерминации R²  используется для проверки статистической значимости в целом уравнения нелинейной регрессии по -критерию Фишера:

,

где  – число параметров при переменных х;  – число наблюдений.

Если , то гипотеза Н₀ о статистической не значимости  уравнения регрессии отклоняется.

Для степенной функции , гиперболы , экспоненты  формула -критерия имеет вид:

.

Для параболы второй степени :

.