95

§ 11. Приложение метода резолюций для анализа силлогизмов Аристотеля.

По Аристотелю «силлогизм же есть речь, в которой при предположении чего-нибудь из него с необходимостью вытекает нечто отличное от утверждённого и, [именно] в силу того, что это есть».

Известно, что каждый силлогизм Аристотеля можно представить как некоторую комбинацию предложений следующих видов:

основании истинности двух посылок указанного вида. Силлогизм обозначают тремя буквами по виду посылки и виду заключения. Так, например, силлогизм ААА можно представить в виде:

всякий М есть P,

всякий Р есть Q,

следовательно, всякий М есть Q.

В зависимости от положения среднего термина в посылках, различают четыре фигуры силлогизма. Модусами силлогизма называются разновидности силлогизма отличающиеся качественной и количественной характеристикой посылок и заключения. Силлогизмам присваивают собственные имена, например, силлогизм ААА называется Barbara (в слове “ Barbara” гласными являются три буквы а).

Можно подсчитать, что количество различных модусов силлогизмов Аристотеля равно 256 (по 64 в каждой фигуре). Сколько же среди этих модусов правильных, когда из истинности посылок следует истинность заключения? Известно, что правильных, модусов 24. Рассмотрим применение метода резолюций для выяснения правильности модусов.

Рассмотрим силлогизм Барбара построенный по первой фигуре. В символьной записи он означает, что из истинности формул

x (S(x) P(x)),x (P(x) Q(x))

нужно получить истинность формулы

x(S(x) Q(x)),

т. е. доказать, что из формул x(S(x) P(x)) и x(P(x) Q(x)) логически следует формула x(S(x) Q(x)). Известно, что если формула

является противоречием, то указанное логическое следствие будет доказано. Так как формула С содержит только одноместные предикатные буквы (S,P,Q), то выяснение противоречие С или нет можно было бы свести к

96

проблеме разрешимости алгебры высказываний. При этом получили бы нетривиальную задачу в силу следующего. В формуле С три предикатные буквы, следовательно, нужно было бы взять множество, содержащее 23 =8 элементов, положим М ={1,2,…,8}. Тогда каждый предикат порождает на М по 8 высказываний: S(1),…,S(8); P(1),…,P(8) ; Q(1),…,Q(8). Следовательно, в

пропозициональной форме, построенной для С, будет 24 переменных и таблица истинности будет содержать 224 строк. Ясно, что составление такой таблицы сложно даже с помощью ЭВМ. При применении метода резолюций вычисления оказываются совсем незначительными.

Следуя указанной в параграфе 10 процедуре, нужно получить сколемовскую стандартную форму Сs для формулы С, которая имеет вид (3.9). Сначала переименуем вхождения х во второй посылке на у, а в заключении силлогизма на z (в первой посылке переменную х не переименовываем). Легко видеть, что первые два дизъюнкта в Сs будут следующими:

1)S(x) P(x),

2)P(у) Q(у)

которые, очевидно, получены из посылок силлогизма. Заключение силлогизма в (3.9) взято с отрицанием: z(S(z) Q(z)). Преобразуя последнюю формулу, получим: z(S(z)& Q(z)). При нахождении сколемовской стандартной формы квантор существования можно вынести первым и затем, удаляя его, вводим постоянную а вместо переменной удаляемого квантора (переменной z). В результате в стандартной форме Сs будут еще два дизъюнкта:

3)S(a),

4)7 Q(a),

которые получены из заключения силлогизма. Теперь к множеству дизъюнктов 1)-4) применяем метод резолюций. Тогда имеем последовательно:

5)P(a) из 3) и 1),

6) P(a) из 4) и 2),

7) из 5) и 6).

Таким образом, получили пустой дизъюнкт, следовательно, силлогизм ААА

верен.

Рассмотрим силлогизм Darii (AII по 3-ей фигуре). В символической записи имеем:

x (P(x) S(x))x (P(x) & Q(x))

---------------------------------

x (S(x) & Q(x)).

Преобразуя, как выше, получим:

1)P(x) S(x)

2)P(a)

3)Q(a)

97

4) S(y) Q(y)

Далее получаем следующие бинарные резольвенты:

5)S(a) из 1) и 2),

6)S(a) из 3) и 4),

7) из 5) и 6).

Следовательно, силлогизм AII верен.

Рассмотрим ещё силлогизм, который в символьной записи имеет вид:

x (P(x) S(x)),x (Q(x) P(x)),

-----------------------------------

x (Q(x) S(x)) .

Преобразовав формулы, получим:

1) P(x) S(x),

2) Q(y) S(y),

3)Q(a),

4)S(a),

Далее получаем бинарную резольвенту:

5) 7P(a) из 2) и 3).

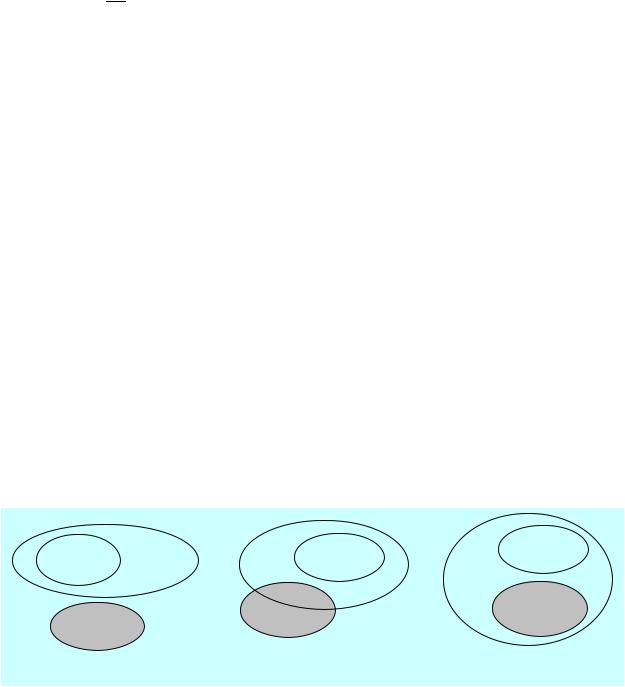
Никаких других резольвент получить нельзя, в том числе нельзя получить пустой дизъюнкт, тогда из теоремы полноты метода резолюций следует, что из посылок не будет (не всегда будет) следовать заключение. Невыполнимость этого силлогизма можно пояснить на Рис. 3.1. Возможны различные варианты расположения областей истинности предикатов, см. Рис. 3.1, на котором области истинности обозначены теми же буквами, что и сами предикаты. В варианте изображённом на Рис. 3.1 а) видно, что из истинности посылок следует истинность заключения. В вариантах изображённых на Рис. 3.1 б), в) из истинности посылок не следует истинность заключения.

§ 12. Использование метода резолюций в языке ПРОЛОГ

Язык программирования ПРОЛОГ существенно опирается на метод

98

резолюций. Само название ПРОЛОГ есть сокращение, означающее программирование в терминах логики. Вычисления на ПРОЛОГе можно рассматривать как доказательство теорем с использованием метода резолюций и применением дизъюнктов специального вида – хорновских дизъюнктов.

Отметим следующую принципиальную отличительную черту языка ПРОЛОГ. В языках программирования таких как АЛГОЛ, ФОРТРАН, C++ описывается как решать ту или иную задачу. Программирование на ПРОЛОГе указывает только что нужно (необходимо) сделать, т.е. указывается цель, а не процедура решения. Программист должен дать определение ситуации и формулировать задачу, а система сама решает задачу. При решении задачи используется метод резолюций.

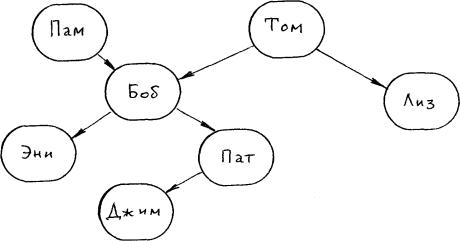
Рассмотрим простейший пример. Пусть задано следующее дерево родственных отношений, изображенное на следующем рисунке 3.2.

Рис.3.2. Дерево родственных отношений.

То, что Том является родителем Боба можно записать на Прологе

так:

родитель (том, боб).

Все приведенное дерево родственных отношений описывается следующей

пролог-программой:

99

родитель (боб, пат). (3.14)

родитель (пат, джим). (3.15)

Отметим, что каждое предложение пролога заканчивается точкой. После ввода такой программы в пролог-систему этой системе можно задавать вопросы, касающиеся отношения родитель. Например, является ли Боб родителем Пата? Этот вопрос ставится следующим образом:

? - родитель (боб, пат).

Далее из (3.14) и (3.16) бинарной резолюцией получаем пустой дизъюнкт , что и означает положительный ответ.

Другим вопросом мог бы быть такой

? - родитель (пам, лиз).

Система ответит

Этот дизъюнкт ни с одним из дизъюнктов (3.10)-(3.15) не дает пустого дизъюнкта. По идеологии вопросно-ответных систем система должна была бы организовать отрицание вопроса, т.е. дизъюнкт:

родитель (пaм, лиз). (3.18)

Но и этот дизъюнкт вместе с (3.10)-(3.15) не порождает пустого дизъюнкта. Следовательно, система должна была бы ответить: "недостаточно информации". Но в реализации ПРОЛОГа этого не будет. Система рассмотрит только дизъюнкты (3.10)-(3.15) и (3.17) и так как они не дают пустой дизъюнкт, то получим ответ: No (нет). Это происходит оттого, что считается, что в программу включены все возможные знания об объектах. Тогда, поскольку нет никакой информации является ли Пам родителем Лиз, то система говорит: No (нет), а не будет строить дизъюнкт (3.18).

Можно задавать и такие вопросы: "Кто является родителем Лиз?" в

виде:

? - родитель (X,лиз).

100

Система ответит: Х = том Покажем, как находится ответ на этот вопрос.

Вопрос, как и выше, можно было бы преобразовать в дизъюнкт:

родитель (Х, лиз).

Здесь имеется переменная Х. Если подставлять вместо Х постоянные (пам, том, боб, пат) и сравнивать с (3.10)-(3.15), можно получить пустой дизъюнкт при Х равном «том». Получится пустой дизъюнкт, означающий, что Х=том истинно, но полученный ответ не сохранится. Для сохранения ответа вводится специальная функция, зависящая от Х, называемая ANSпредикатом (от answer – ответ).

Следовательно, к исходным дизъюнктам (3.10)-(3.15) нужно добавить дизъюнкт соответствующий вопросу:

Применяя метод резолюций из (3.12) и (3.19) система получит: ANS(том) и выдаст результат (на печать): Х=том

Вопрос: "Кто дети Боба?" можно передать системе в виде:

?- родитель (боб,Х).

Вданном случае ответ не единственен.

Взависимости от вариантов ПРОЛОГа система может выдавать один из ответов, например:

Х = пат

иждать введения точки с запятой, после чего выдает второй ответ:

X = эни

В других реализациях ПРОЛОГа могут выдаваться последовательно все возможные ответы без дополнительного запроса.

Системе можно задавать и другие вопросы, например,

1)"Кто родитель Боба?":

?- родитель (X,боб).

Система ответит: Х = пам; Х=тoм

2)"Кто чей родитель?":

?- родитель (Х,Y).

Система распечатает возможные значения Х и Y.

3) "Кто внуки Тома? Так как в системе не введено понятие внуков, то строим сложный вопрос.

?-родитель (том, Х ), родитель (X, Y).

Запятая между предложениями воспринимается как конъюнкция. Составной вопрос интерпретируется: найти X,Y, удовлетворяющие двум требованиям

родитель(том,X) и родитель (X,Y).

Конъюнкция коммутативна, поэтому можно вопрос сформулировать и иначе

?-родитель(X,Y), родитель(том,X)