Методические указания к выполнению

КОНТРОЛЬНОЙ РАБОТЫ

Часть 2.3

Основные законы и формулы

Теория Бора

1.Момент импульса электрона ( второй постулат Бора)

L_n =m v_n r_n= n(h/2),

где m- масса электрона; v_n- скорость электрона на n-й орбите;

r_n – радиус n-ой стационарной орбиты; h- постоянная Планка;

n- главное квантовое число (n=1,2….).

2.Радиус n-й стационарной орбиты:

r_n = a_o n²,

где a_o=0,529 ^. 10^-10 м –первый Боровский радиус.

3.Энергия электрона в атоме водорода.

E_n = - E_i /n²,

где Е_i- энергия ионизации атома водорода.

4.Энергия , излучаемая атомом водорода.:

E = (h/2) = E_n2-E_n1 = E_i (1/n - 1/n),

где n₂ и n₁ – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.

5.Спектроскопическое волновое число:,

где λ – длина волны излучения или поглощения атомом,

R – постоянная Ридберга.

Волновые свойства частиц.

6.Длина волны де Бройля:

где p – импульс частицы.

7.Импульс частицы и его связь с кинетической энергией Т:

а) p=m;

б) p=m=,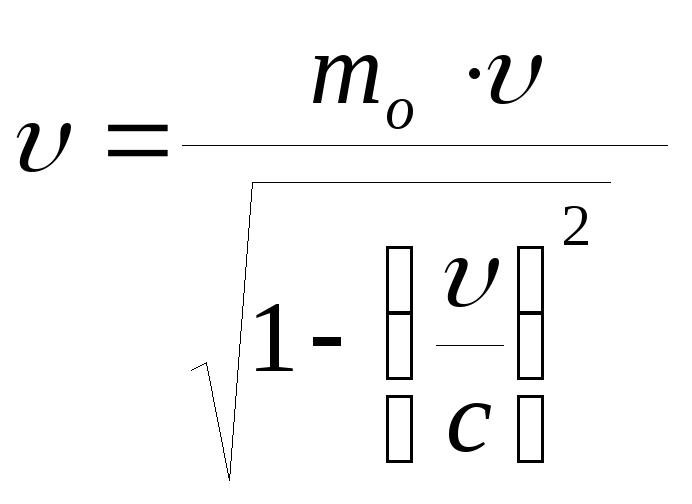

где m_o –масса покоя частицы; m- релятивистская масса;

- скорость частицы; с- скорость света в вакууме;

- энергия покоя частицы.

8.Соотношение неопределённостей:

а) для координаты и импульса:

,

где - неопределённость проекции импульса на осьx ;

неопределённость координаты.

б) для энергии и времени:

,

где- неопределённость энергии;

-время жизни квантовой системы в данном энергетическом состоянии.

9.Одномерное уравнение Шредингера для стационарных состояний:

,

где - волновая функция, описывающая состояние частицы,

m- масса частицы, Е – полная энергия, U – потенциальная энергия частицы.

10.Плотность вероятности:

,

где - вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участкеdx.

11.Вероятность обнаружения частицы в интервале от х₁ до х₂;

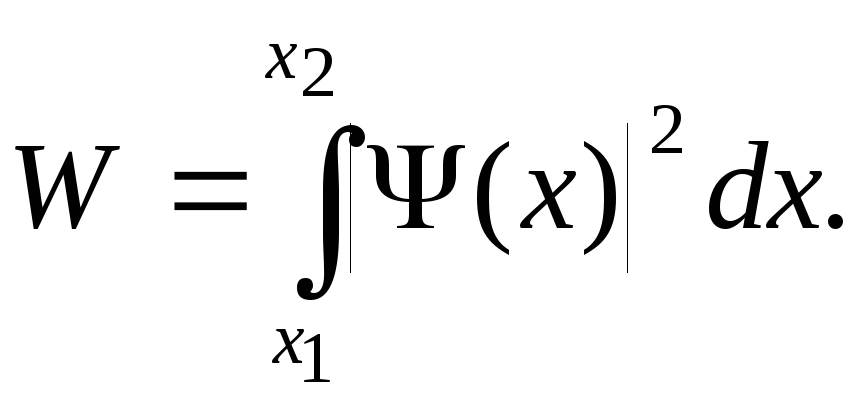
12.Решение уравнения Шредингера для микрочастицы в одномерном бесконечно глубоком прямоугольном потенциальном ящике:

а) собственные нормированные волновые функции:

б) собственные значения энергии:

,

где n =1,2,3,…- квантовое число, - ширина ящика,- масса микрочастицы.

.

Пространственная решётка кристалла.

13.Молярный объём кристалла:

,

где - молярная масса;- плотность кристалла.

14.Объём элементарной ячейки для решётки кубической сингонии:

,

где – параметр решётки.

15.Число элементарных ячеек в одном моле кристалла:

.

16.Если кристалл состоит из одинаковых атомов, то

,

где - число одинаковых атомов, приходящихся на элементарную ячейку;N_A - постоянная Авогадро.

17.Число элементарных ячеек в единице объёма кристалла:

.

18.Если кристалл состоит из одинаковых атомов, то

19.Параметр кубической решётки из одинаковых атомов:

20.Расстояние между соседними атомами в кубической решётке:

а) d= ( гранецентрированной);

б) d= (объёмноцентрированной).

Полупроводники.

21.Удельная проводимость собственных полупроводников:

где – элементарный заряд;

- концентрация носителей заряда ( электронов и дырок);

и - подвижности электронов и дырок ,соответственно.

22.Напряжение на гранях прямоугольного образца при эффекте Холла (холловская разность потенциалов):

U_H=R_HBja,

где R_H- постоянная Холла, В – магнитная индукция,

j- плотность тока, а – ширина пластины (образца).

23.Постоянная Холла для полупроводников типа алмаз, германий, кремний и др., обладающих носителями заряда одного вида (n или р);

R_H = ,

где - концентрация носителей заряда.

Атомное ядро. Радиоактивность.

24.Массовое число ядра (число нуклонов в ядре) :

A = Z + N ,

где Z – зарядовое число (число протонов);

N- число нейтронов.

25.Закон радиоактивного распада:

dN = - Ndt или N = N₀ ,

где dN - число ядер, распадающихся за интервал времени dt;

N – число ядер, нераспавшихся к моменту времени t;

N_o – число ядер в начальный момент (t=0); λ- постоянная радиоактивного распада.

26.Число ядер, распавшихся за время t :

27.В случае , если интервал времени ∆t, за который определяется число распавшихся ядер, много меньше периода полураспада

, то число распавшихся ядер можно определить по формуле

28.Зависимость периода полураспада от постоянной радиоактивного распада:

29.Среднее время жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшается в

e раз.

30.Число N атомов, содержащихся в радиоактивном изотопе:

,

где m- масса изотопа;

- молярная масса;

N_A – постоянная Авогадро.

31.Активность А радиоактивного изотопа:

,

где dN- число ядер, распадающихся за интервал времени dt;

А_о – активность изотопа в начальный момент времени.

32.Удельная активность изотопа:

.

33.Дефект массы ядра:

,

где Z – зарядовое число (число протонов в ядре ); А- массовое число (число нуклонов в ядре ); -масса протона ;- масса нейтрона ;- масса ядра .

34.Энергия связи ядра :

,

где ∆m- дефект массы ядра ; с – скорость света в вакууме.

35.Во внесистемных единицах энергия связи ядра равна

МэВ,

где дефект массы ∆m в а.е.м.; 931 – коэффициент пропорциональности (1 а.е.м. ~ 931 МэВ)