
- •28. Ряды
- •28.1. Числовые ряды. Знакоположительные ряды
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.2. Знакопеременные числовые ряды
- •Задания
- •Задания
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.5. Ряд Фурье
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.6. Интеграл Фурье
- •Задания
- •I уровень
- •II уровень
- •III уровень
Задания
I уровень
1.1. Разложите в ряд Фурье периодическую функцию (с периодом 2). Запишите первые три его слагаемых. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
1.2.Разложите
в ряд Фурье функцию, заданную на промежутке![]() как на полупериоде:
как на полупериоде:
а) по синусам; б) по косинусам.
Запишите первые три члена полученного ряда. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
7)
 8)
8)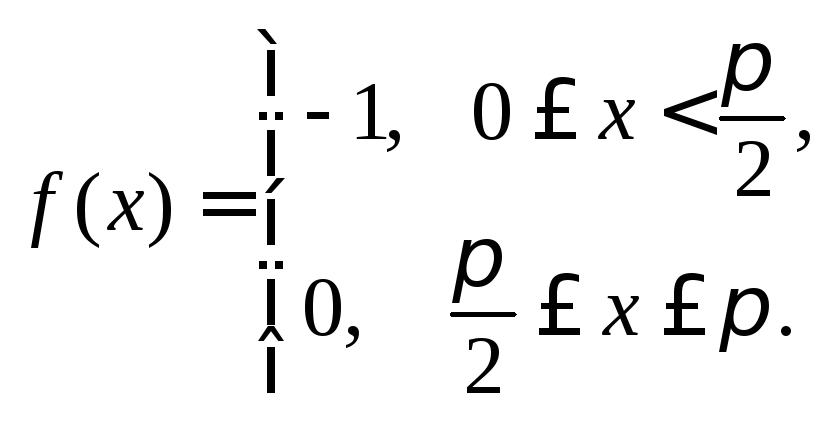
II уровень
2.1. Разложите в ряд Фурье периодическую функцию (с периодом 2). Запишите первые три его слагаемых. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
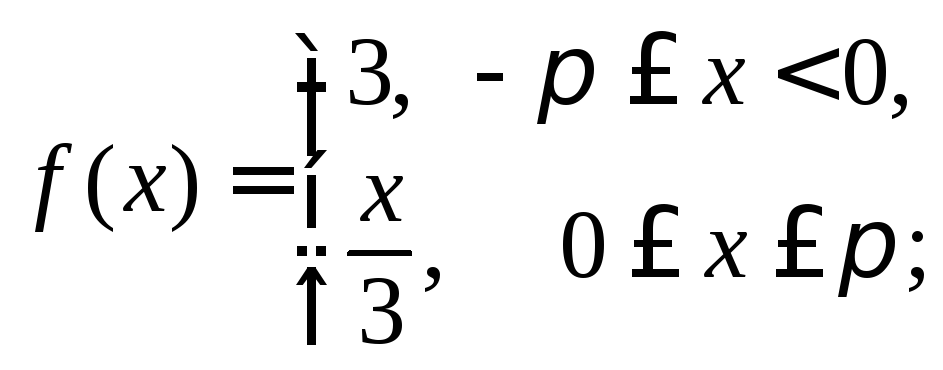 6)
6)

7)
![]() 8)
8)
![]()
2.2.Разложите в ряд Фурье функцию, заданную на промежутке [0; l], как на полупериоде:
а) по синусам; б) по косинусам.
Запишите первые три члена полученного ряда. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
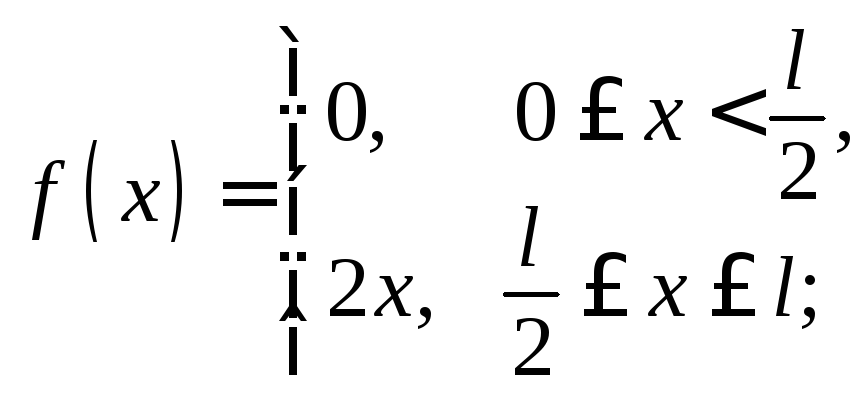 8)
8)
2.3.Разложите в ряд Фурье 2l-периодическую функцию. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда.
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
2.4. Разложите в ряд Фурье функцию, заданную на промежутке, как на полупериоде, продолжив ее четным и нечетным образом. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
III уровень
3.1. Разложите в ряд Фурье функцию, заданную на указанном промежутке, как на полупериоде:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]()
3.2. Разложите в ряд Фурье периодическую функцию (с периодом 2). Запишите первые три его слагаемых. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
4)
![]() 5)
5)![]()
6)
![]()
3.3.Разложите в ряд Фурье 2l-периодическую функцию. Исследуйте ряд на сходимость:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
3.4. Разложите в ряд Фурье функцию, заданную на промежутке, как на полупериоде, продолжив ее четным и нечетным образом. Исследуйте ряд на сходимость. Постройте графики данной функции и суммы ряда:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
28.6. Интеграл Фурье
Если функция f(x) определена на всей числовой оси, абсолютно интегрируема на бесконечном промежутке, и удовлетворяет условиям теоремы Дирихле в любом конечном промежутке, то справедливо следующее интегральное представление функции f(x):
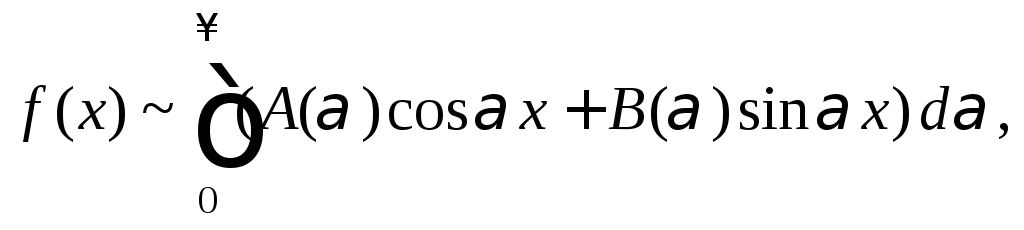 (28.34)
(28.34)
где
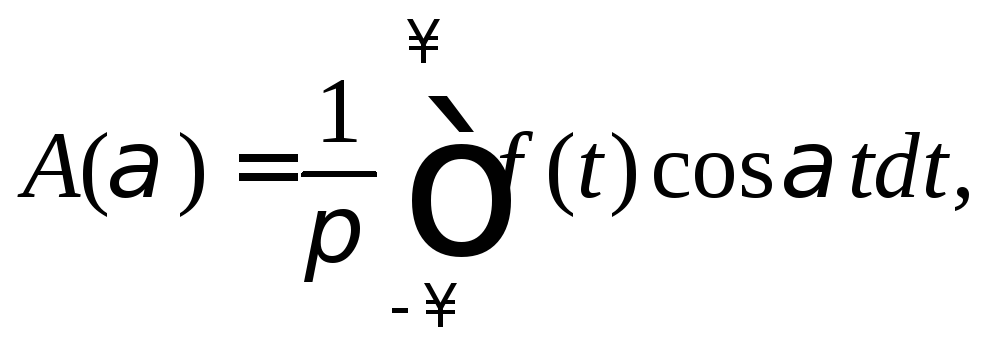

которое называется интегралом Фурье для функции f(x).
Интеграл Фурье
для функцииf(x)сходится к самой функции в точках
непрерывности. В каждой точке разрыва![]() функции ее интеграл Фурье
сходится к полусумме односторонних
пределов функции при стремленииxк
функции ее интеграл Фурье
сходится к полусумме односторонних
пределов функции при стремленииxк![]() слева и справа, т. е.
дает значение, равное
слева и справа, т. е.
дает значение, равное![]()
Комплексная форма интеграла Фурье:
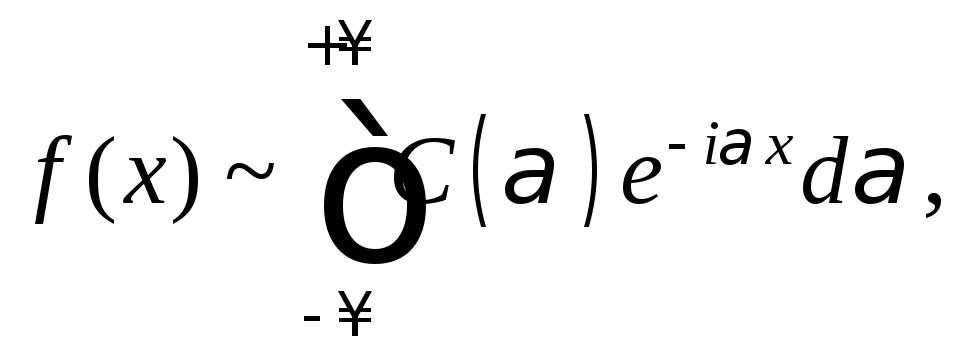 (28.35)
(28.35)
где
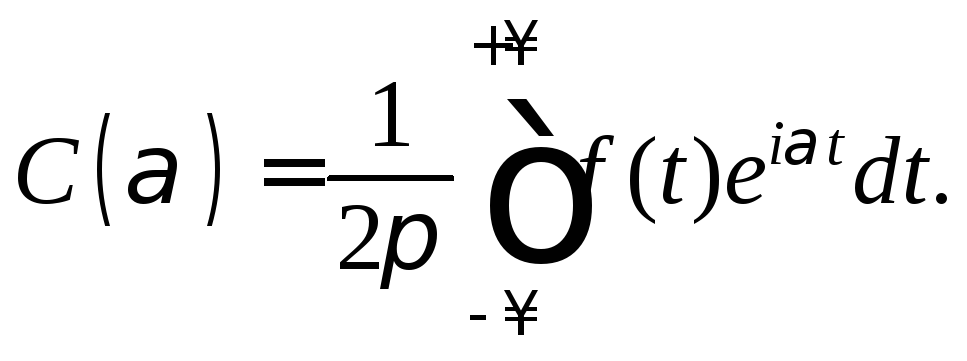
Частные случаи представления функции f(x) интегралом Фурье
1. Если
функцияf(x)являетсячетной![]() то ееинтеграл Фурье содержит только
косинусы:
то ееинтеграл Фурье содержит только
косинусы:

![]()
 (28.36)
(28.36)
2. Если
функцияf(x)являетсянечетной![]() то ееинтеграл Фурье содержит только
синусы:
то ееинтеграл Фурье содержит только
синусы:
![]()
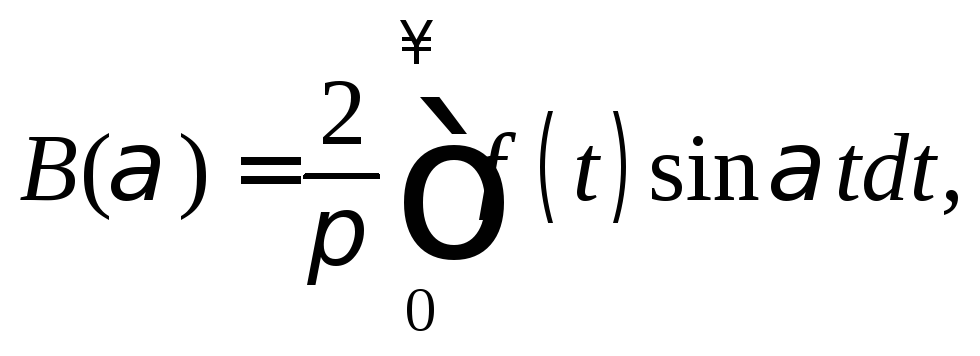
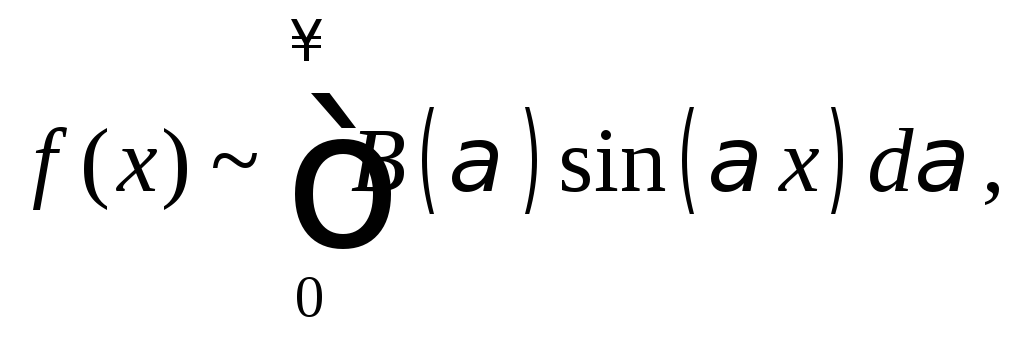 (28.37)
(28.37)
3. Если
функция f(x)
задана на промежутке
![]() то ее интеграл
Фурье может
быть получен следующими двумя способами:
то ее интеграл
Фурье может
быть получен следующими двумя способами:
а) по формуле
(28.36) при четном продолжении функции на
промежутке
![]() (график данной функции продолжается на
промежутке
(график данной функции продолжается на
промежутке![]() симметрично относительно оси ординат,
рис. 28.14),
симметрично относительно оси ординат,
рис. 28.14),
Рис. 28.14
б) по формуле
(28.37) при нечетном продолжении функции
на промежутке
![]() (график данной функции продолжается на
промежутке
(график данной функции продолжается на
промежутке![]() симметрично относительно начала
координат, рис. 28.15).
симметрично относительно начала
координат, рис. 28.15).

Рис. 28.15
Пример 1. Заданную функцию представить в виде интеграла Фурье.
1)
![]() 2)
2)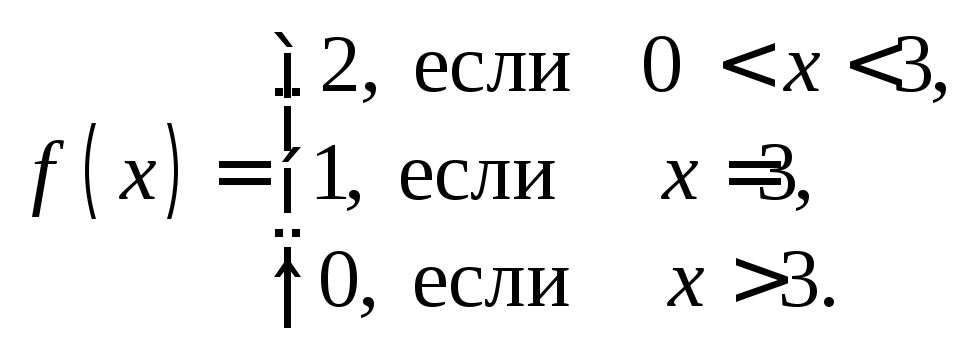
Решение. 1) Заданная функция нечетная (рис. 28.16)

Рис. 28.16
Поэтому,
согласно формуле (28.37),
![]()
Вычисляем:
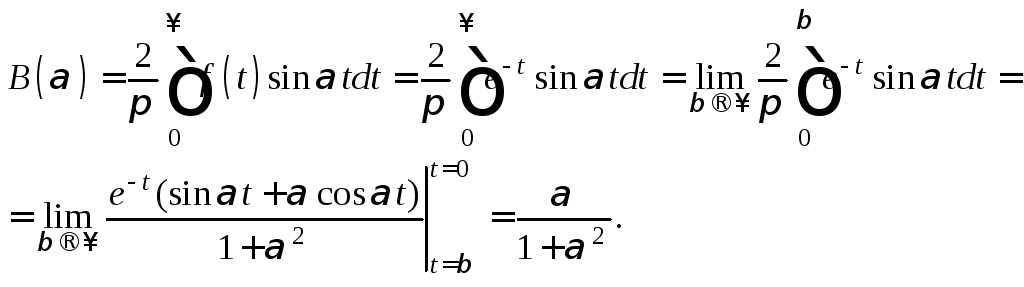
Тогда
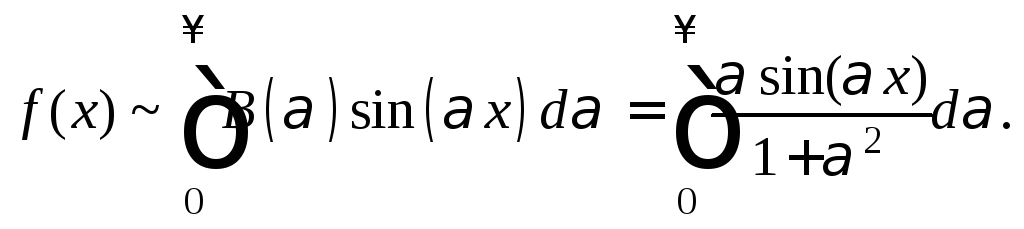
На
всей числовой оси, кроме точки
![]() интегралФурье
сходится к функции
f(x),
а в точке
интегралФурье
сходится к функции
f(x),
а в точке
![]() интегралФурье
равен
интегралФурье
равен
![]()
2)
Заданная функция f(x)
определена только на промежутке
![]() поэтому ее можно представить интегралом
Фурье двумя способами:
поэтому ее можно представить интегралом
Фурье двумя способами:
1-й
способ. При
четном продолжении заданной
функции f(x)
на промежутке
![]() (рис. 28.17), согласно формуле (28.35), получим:
(рис. 28.17), согласно формуле (28.35), получим:

![]()
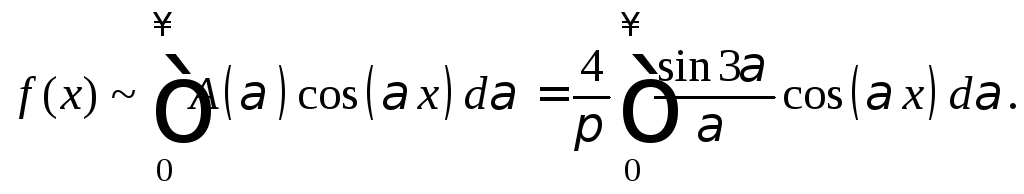

Рис. 28.17
2-й
способ.
При нечетном продолжении заданной
функции f(x)
на промежутке
![]() (рис. 28.18), согласно формуле (28.36), получим:
(рис. 28.18), согласно формуле (28.36), получим:
![]()
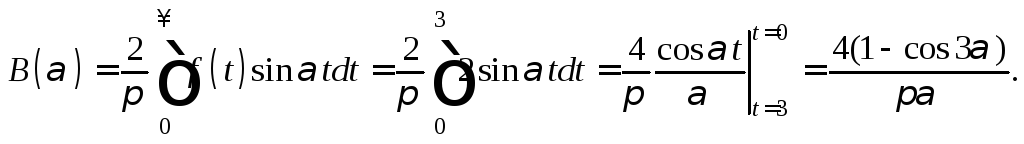
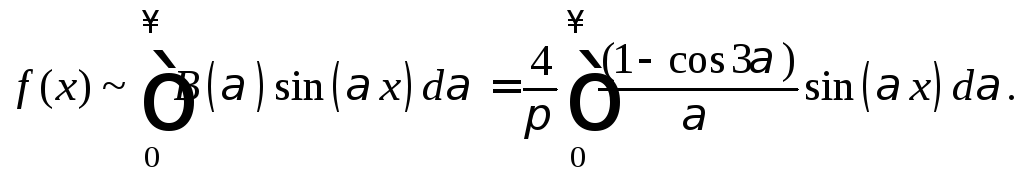

Рис. 28.18
Оба
полученных интеграла Фурье представляют
заданную функцию во всей области ее
определения, включая и точку
![]() в которой функция имеет разрыв, поскольку
в этой точке значение каждого из
полученных интегралов равно:
в которой функция имеет разрыв, поскольку
в этой точке значение каждого из
полученных интегралов равно:
![]()
