Задания

I уровень

1.1. Найдите область сходимости функционального ряда:

1) 2)3)4)

5) 6)7)8)

II уровень

2.1. Найдите область сходимости функционального ряда:

1) 2)3)

4) 5)6)

7) 8)

III уровень

3.1. Найдите область сходимости функционального ряда:

1) 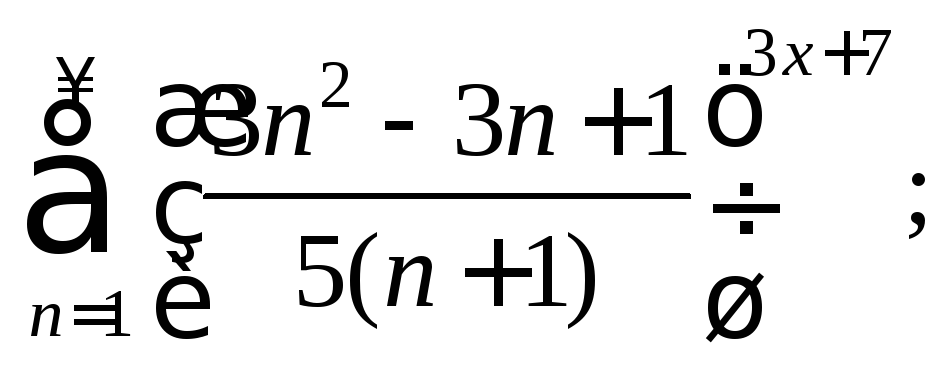2)

3) 4)

5) 6)

7) 8)

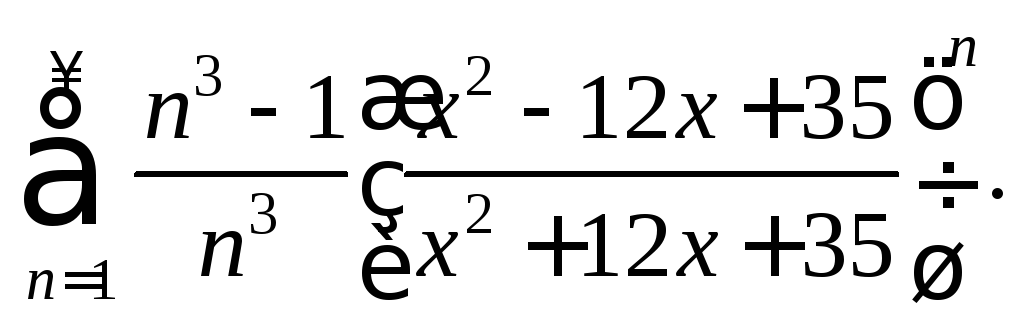
28.4. Степенные ряды

Cтепенным рядом называется функциональный ряд вида

(28.18)

где числа– коэффициенты ряда.

Ряд (28.18) также называется степенным рядом с центром в точке a.

Для степенного ряда находят радиус сходимости rпо одной из формул

(28.19)

если эти пределы существуют.

Ряд (28.18) сходится, причем абсолютно, на интервале сходимостигдеи расходится наПриряд (28.18) сходится только в точкеa, при– на всей числовой оси.

Для определения области сходимости заданного степенного ряда следует найти его радиус сходимости по формулам (28.19),далее определить его интервал сходимости и выяснить, сходится или расходится ряд в граничных точках этого интерваладля чего эти значения подставляют в заданный ряд и исследуют полученные числовые ряды.

Замечание. Поскольку степенной ряд является функциональным, то для определения области сходимости степенного ряда можно также использовать признаки абсолютной сходимости Д’Аламбера или Коши, а затем те значения x, для которых эти признаки не решают вопрос о сходимости ряда исследуются отдельно с использованиемдостаточных признаков сходимости числовых рядов (см. параграф 28.3). Однако целесообразно решать эту задачу через нахождение радиуса сходимости r.

Свойства степенных рядов

1.СуммаS(x) степенного ряда является непрерывной функцией на его интервале сходимости.

2.Степенной ряд с суммойS(x) можно почленно дифференцировать и интегрировать на его интервале сходимости любое количество раз:

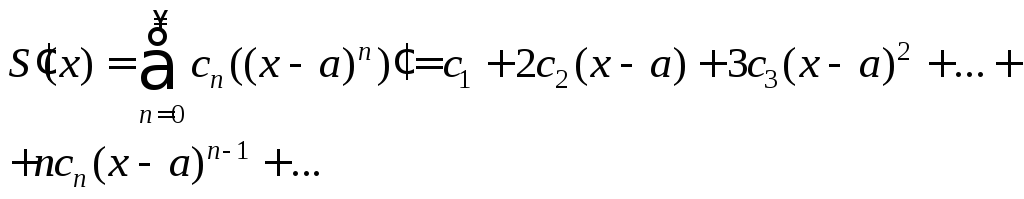
Интервал сходимости при этом не меняется. Сходимость может измениться только в граничных точках интервала сходимости.

Операции почленного дифференцирования и интегрирования позволяют в некоторых случаях найти сумму степенного ряда.

Если существует такой степенной ряд (28.18), который на определенном промежутке Dсходится к функцииf(x), то говорят, чтофункция f(x) разлагается на промежутке D в степенной ряд (по степеням x – a),а выражение вида

, (28.20)

где называетсяразложением функции в степенной ряд (по степеням x – a). Такое разложение единственно.

Рядом Тейлора функции f(x) в окрестности точки a (по степенямx – a),называется степенной ряд вида

(28.21)

Критерий сходимости ряда Тейлора.Ряд Тейлора (28.21) функцииf(x) сходится к ней на некотором интервалетогда и только тогда, когда остаточный членформулы Тейлора для функцииf(x) при всехстремится к нулю с ростомn:

Признак сходимости ряда Тейлора.Если в интервалефункцияf(x) бесконечно дифференцируема и все ее производные ограничены в совокупности, то в этом интервале функцияf(x) разлагается в ряд Тейлора по степеням(является его суммой).

Рядом Маклорена функции f(x) называется ряд Тейлора (28.21)функцииf(x) в окрестности точки(по степенямx):

(28.22)

На области сходимости ряды Маклорена для основных элементарных функций имеют указанный ниже вид:

При разложении функции f(x) в ряд используют следующие правила:

1) непосредственное разложение функции f(x) в ряд Тейлора (28.21)или Маклорена (28.22);

2) использование известных рядов Маклорена для основных элементарных функций;

3) использование сложения и вычитания рядов и умножения ряда на число;

4) использование дифференцирования и интегрирования рядов.

Пример 1. Найти область сходимости степенного ряда:

1) 2)

3) 4)

Решение. 1) Формула коэффициентов ряда:

По формуле (28.19) найдем радиус сходимости степенного ряда:

Поэтому (–1; 1) является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (–1; 1). При получаем гармонический ряд, который расходится:

.

При получаем знакочередующийся ряд, который сходится по признаку Лейбница:

.

Следовательно, областью сходимости данного ряда является полуоткрытый интервал

2) Имеем степенной ряд с центром в точке

Формула коэффициентов ряда

По формуле (28.19) найдем радиус сходимости степенного ряда:

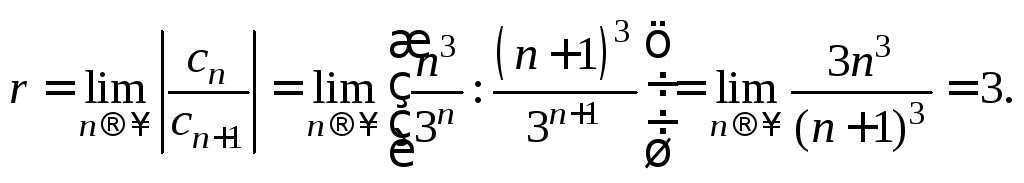
Поэтому является интервалом сходимости данного ряда. Исследуем сходимость ряда на концах интервала (–4; 2). При получаем знакочередующийся рядкоторый расходится, поскольку для него не выполняется необходимый признак сходимости:

При получаем знакоположительный ряд

который также расходится, поскольку для него не выполняется необходимый признак сходимости.

Следовательно, областью сходимости заданного ряда является открытый интервал: (–4; 2).

3) Имеем степенной ряд с центром в точке Формула коэффициентов рядаПо формуле (28.19) найдем радиус сходимости степенного ряда:

Следовательно, областью сходимости заданного ряда является вся числовая ось:

4) Имеем степенной ряд с центром в точке Формула коэффициентов ряда:По формуле (28.19) найдем радиус сходимости степенного ряда:

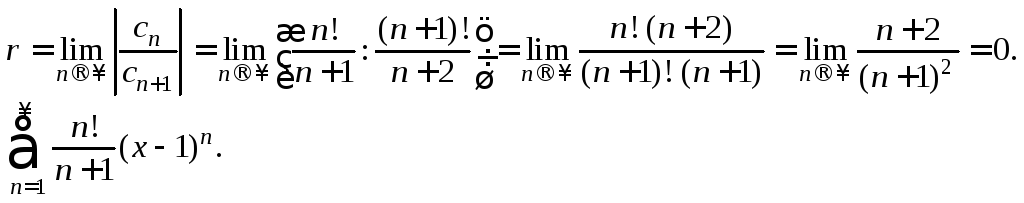
Следовательно, заданный ряд сходится только в точке

Пример 2. Найти сумму ряда и указать область сходимости:

1) 2)

Решение. 1) Интервал сходимости заданного ряда: (– 1; 1). Значит, его можно почленно дифференцировать и интегрировать в его интервале сходимости. Выполним дифференцирование:

Полученный ряд представляет собой сумму бесконечно убывающей при геометрической прогрессии:

откуда

Таким образом, сумма заданного ряда

2) Область сходимости заданного ряда [–1; 1], что следует из признака абсолютной сходимости Д’Аламбера и сходимости ряда при (убедитесь в этом самостоятельно). Значит, его можно почленно дифференцировать и интегрировать в его интервале сходимости:

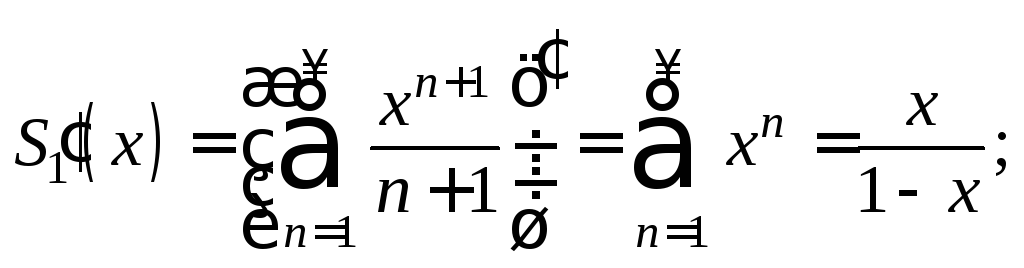
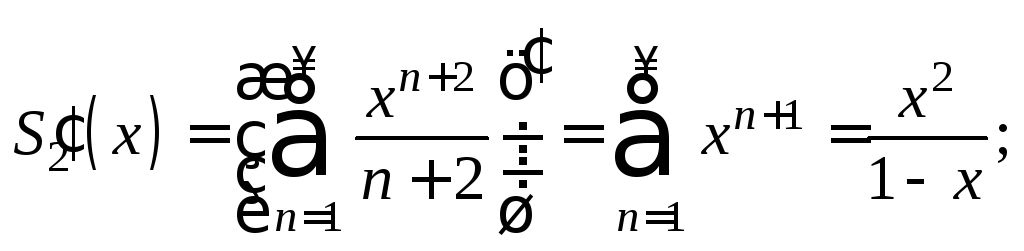
Окончательно имеем:

Пример 3. Разложить функцию в ряд Тейлора по степенямx.

Решение. Используем прием непосредственного разложения.

Составим для данной функции ряд Тейлора. С этой целью найдем числовые значения производных всех порядков функции в точке

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Подставив найденные значения производных в выражение (28.21) при получим ряд Тейлора для функциипо степенямx:

По формуле (28.19) найдем радиус сходимости полученного степенного ряда:

Следовательно, областью сходимости данного ряда является вся числовая ось:

Пример 4. Разложить функцию в ряд Маклорена.

Решение. Полагаем и используем известное разложение в ряд Маклорена для функции

.

Тогда, с учетом того, что получаем:

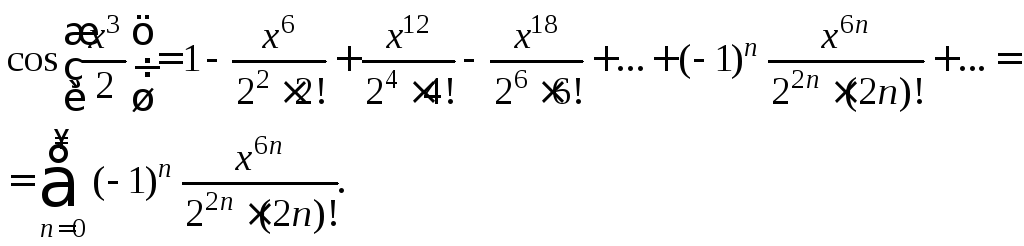
Так как разложение в ряд Маклорена функции имеет место для всехто и разложение в ряд Маклорена заданной функцииимеет место для всех

Пример 5. Разложить в ряд по степеням x функцию

Решение. Замечаем, что функцию можно получить интегрированием функции Поэтому разложим в ряд по степенямx функцию и затем проинтегрируем полученный степенной ряд. Посколькуиспользуем табличное разложение для функции

Полагая получим:

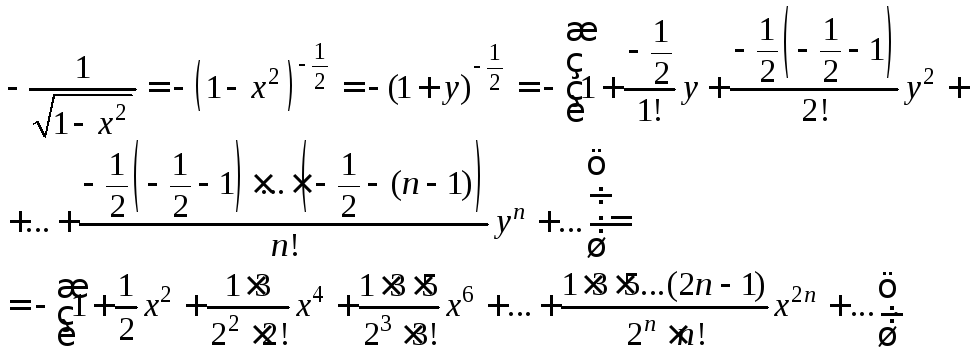
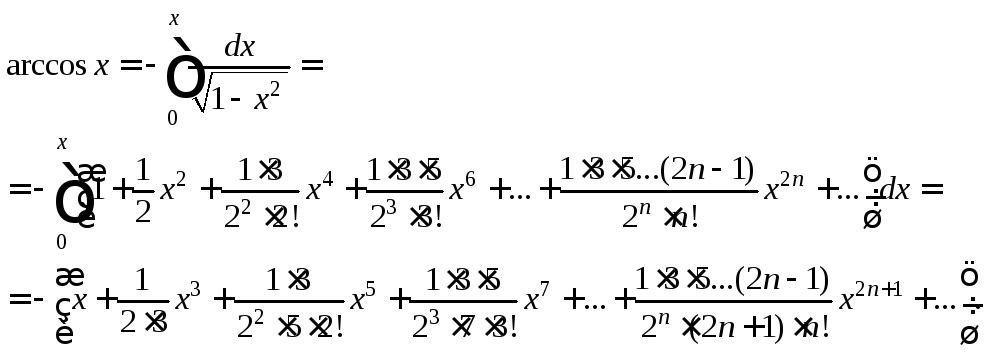
Так как при интегрировании интервал сходимости степенного ряда не меняется, то найденное разложение имеет место для

Пример 6. Разлагая функцию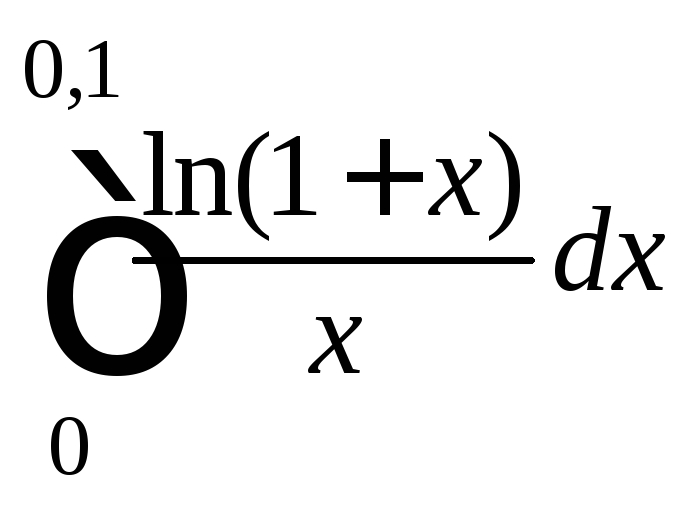в ряд, вычислить с точностью 0,001.

Решение. Используя разложение в степенной ряд, получим

Мы взяли два слагаемых, так как третье по модулю меньше требуемой точности Поэтому, начиная с третьего, все последующие слагаемые отбрасываем.