
- •28. Ряды
- •28.1. Числовые ряды. Знакоположительные ряды
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.2. Знакопеременные числовые ряды
- •Задания
- •Задания
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.5. Ряд Фурье
- •Задания
- •I уровень
- •II уровень
- •III уровень
- •28.6. Интеграл Фурье
- •Задания
- •I уровень
- •II уровень
- •III уровень
Задания
I уровень
1.1. Напишите пять первых членов ряда, и проверьте, выполняется ли для него необходимый признак сходимости:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
1.2. Исследуйте сходимость ряда по признакам сравнения:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
1.3. Исследуйте сходимость ряда по признаку Д’Аламбера:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
1.4. Исследуйте сходимость ряда по признаку Коши:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
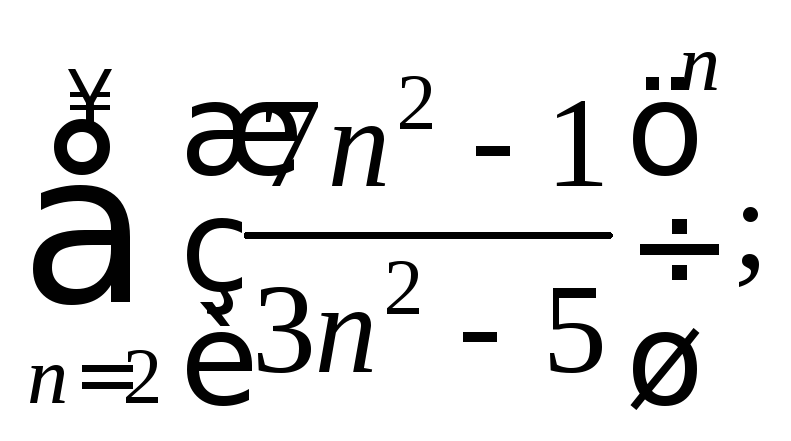 5)
5)![]() 6)
6)![]()
1.5. Исследуйте сходимость ряда по интегральному критерию:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
II уровень
2.1. Найдите сумму ряда:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
2.2. Исследуйте сходимость ряда по признакам сравнения:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
2.3. Исследуйте сходимость ряда по признаку Д’Аламбера:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
2.4. Исследуйте сходимость ряда по признаку Коши:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
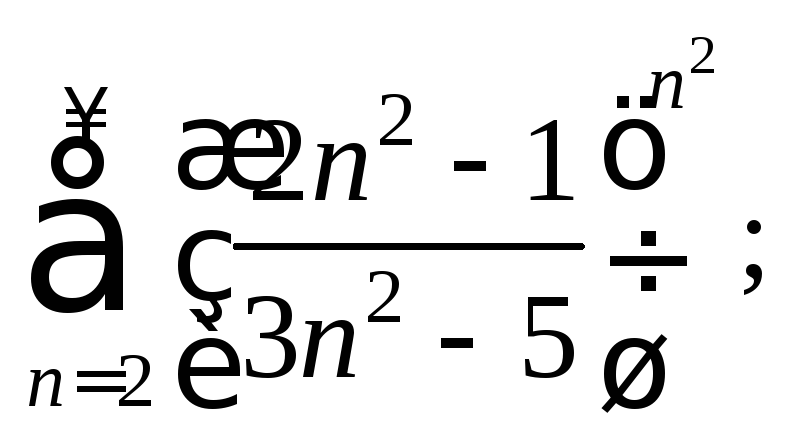 5)
5)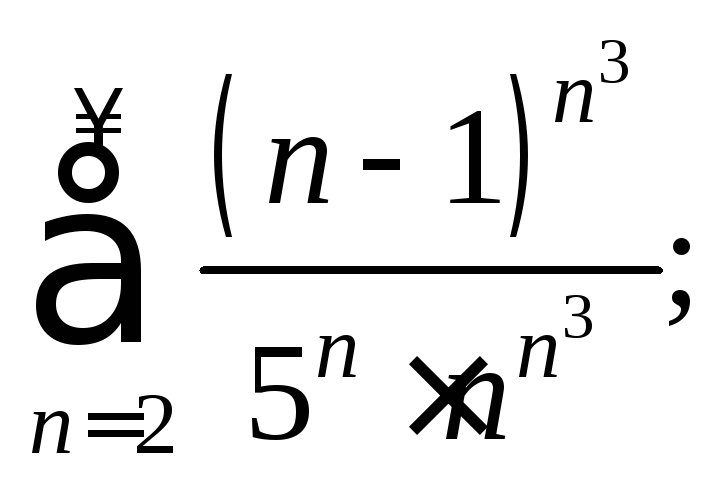 6)
6)![]()
2.5. Исследуйте сходимость ряда по интегральному критерию:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
2.6. Исследуйте сходимость ряда с положительными членами:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)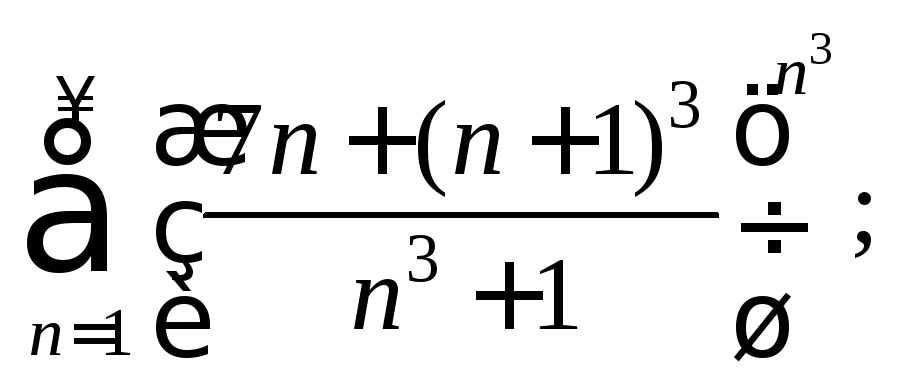
9)
![]() 10)
10)![]()
III уровень
3.1. Найдите сумму ряда:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() .
.
3.2. Исследуйте сходимость ряда с положительными членами:
1)
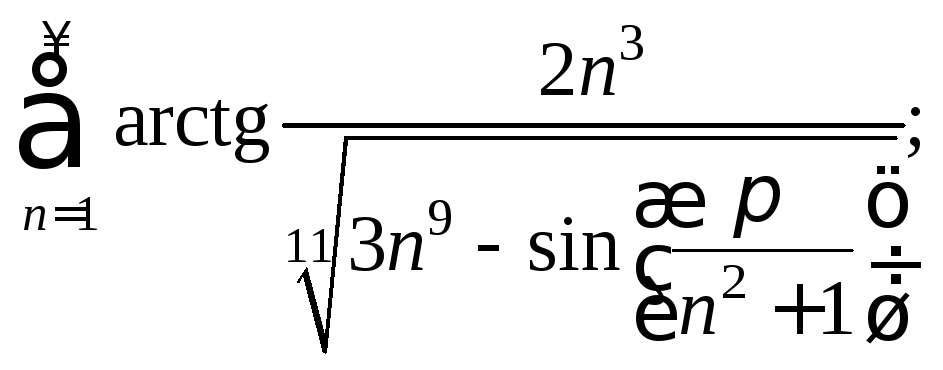 2)
2)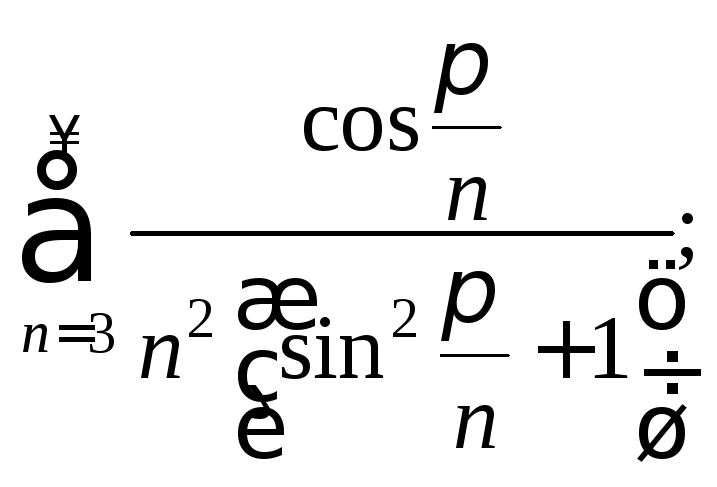
3)
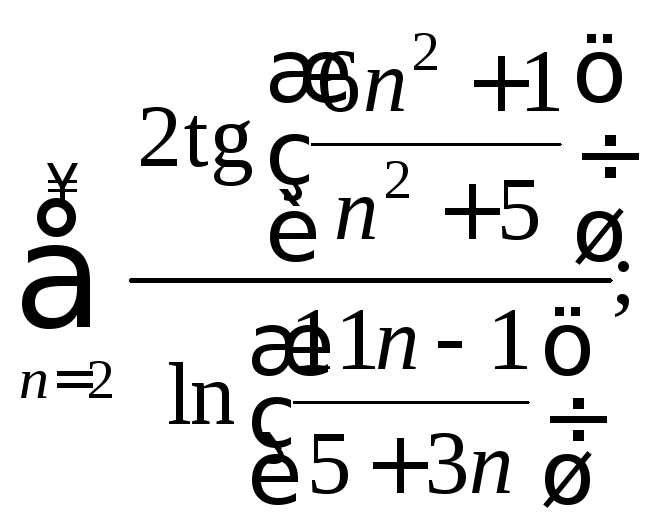 4)
4)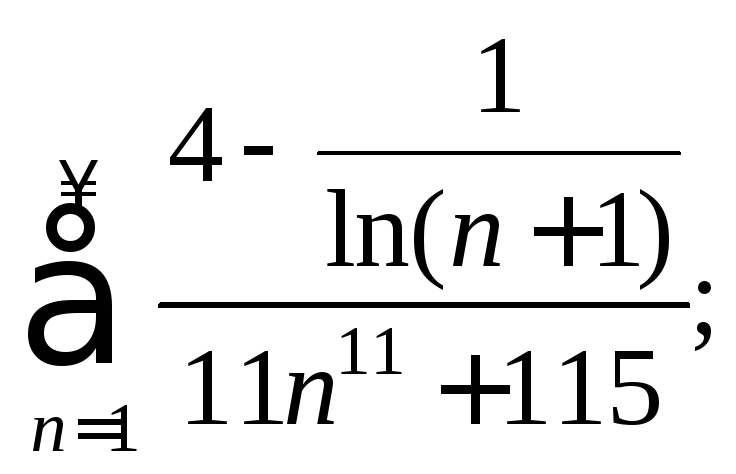
5)
![]() 6)
6)![]()
7)
![]() 8)
8)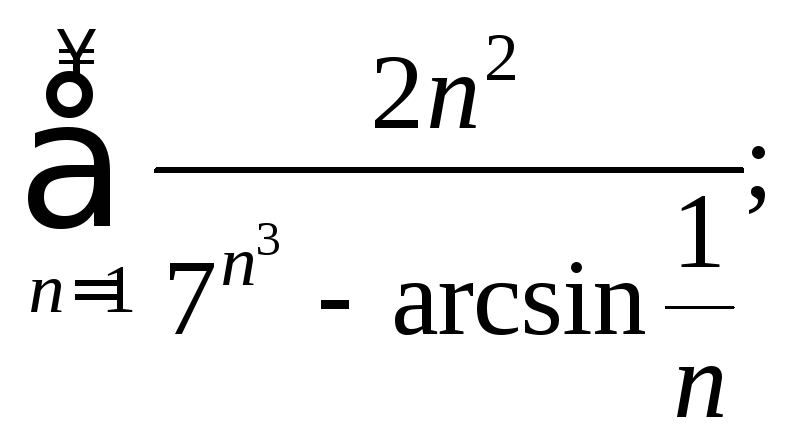
9)
![]() 10)
10)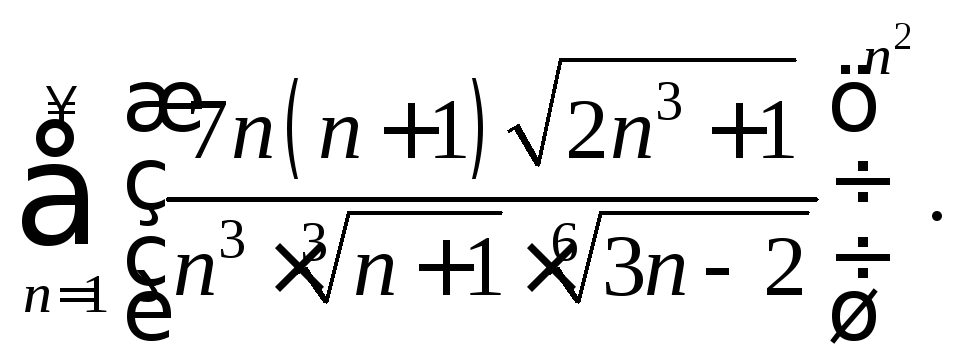
28.2. Знакопеременные числовые ряды
Для знакопеременного ряда
![]() (28.9)
(28.9)
составляют ряд из абсолютных значений его членов, т. е.
![]() (28.10)
(28.10)
Для исследования на сходимость ряда (28.10) используют признаки сходимости знакоположительных рядов.
Знакопеременный ряд (28.9) называется абсолютно сходящимся, если сходится ряд (28.10).
Теорема.Всякий абсолютно сходящийся ряд сходится.
Если знакопеременный ряд не сходится абсолютно, то нельзя утверждать, что он не сходится. Необходимо провести дополнительное исследование.
Знакопеременный ряд называется условно сходящимся, если он сходится, но не сходится абсолютно.
Для исследования на сходимость знакопеременного ряда вида
![]() (28.11)
(28.11)
используют следующие две теоремы.
Признак Дирихле. Пусть для ряда (28.11) выполняются условия:
1) последовательность
частичных сумм ряда
![]() является ограниченной;
является ограниченной;
2)
последовательность
![]() монотонно
убывает, стремясь к нулю.
монотонно
убывает, стремясь к нулю.
Тогда ряд (28.11) сходится.
Признак Абеля. Пусть для ряда (28.11) выполняются условия:
1) последовательность
![]() является монотонной и ограниченной;
является монотонной и ограниченной;
2) ряд
![]() сходится.
сходится.
Тогда ряд (28.11) сходится.
Важным частным случаем знакопеременного ряда является знакочередующийся ряд.
Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки.
Признак Лейбница.Пусть для знакочередующегося ряда
![]() (28.12)
(28.12)
где
![]()
![]() выполняются условия:
выполняются условия:
1) абсолютные значения его членов образуют монотонно невозрастающую последовательность, т. е.
![]()
2)
![]()
Тогда ряд (28.12) сходится.
Ряд, удовлетворяющий условиям признака Лейбница, называется рядом Лейбница.
С
л е д с т в и е 1. Если для знакочередующегося
ряда (28.12) выполняются условия признака
Лейбница, то для его суммы S
справедлива оценка
![]()
С
л е д с т в и е 2. Для остатка
![]() знакочередующегося ряда, который
удовлетворяет признаку Лейбница,
справедлива оценка
знакочередующегося ряда, который
удовлетворяет признаку Лейбница,
справедлива оценка![]()
![]()
Пример 1. Исследовать сходимость знакопеременного ряда (определить, является ли он абсолютно сходящимся, условно сходящимся или расходящимся):
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Решение.
1)
Чтобы установить, сходится ли заданный
ряд абсолютно, исследуем знакоположительный
ряд
![]() составленный из абсолютных величин
членов данного ряда. Воспользуемся
предельным признаком сравнения с
расходящимся гармоническим рядом
составленный из абсолютных величин
членов данного ряда. Воспользуемся
предельным признаком сравнения с
расходящимся гармоническим рядом![]()
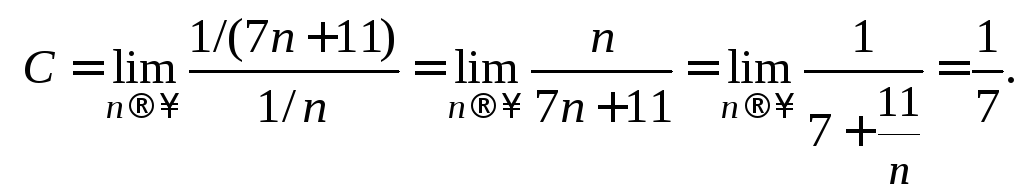
Получен
конечный, отличный от нуля предел.
Сравниваемые ряды ведут себя одинаково.
Поэтому, согласно предельному признаку
сравнения, знакоположительный ряд из
модулей расходится. Для исследования
на условную сходимость используем
признак Лейбница. Поскольку члены
данного знакочередующегося ряда убывают
по абсолютному значению, стремясь к
нулю:
![]() и
и![]() то, согласно признаку Лейбница, заданный
ряд сходится. Следовательно, заданный
ряд является условно сходящимся.
то, согласно признаку Лейбница, заданный
ряд сходится. Следовательно, заданный
ряд является условно сходящимся.
2)
Исследуем знакоположительный ряд
![]() составленный из абсолютных величин
членов данного знакопеременного ряда.
Поскольку
составленный из абсолютных величин
членов данного знакопеременного ряда.
Поскольку![]() то воспользуемся признаком сравнения
с рядом
то воспользуемся признаком сравнения
с рядом![]() который, согласно предельному признаку
Д’Аламбера, сходится. Действительно:
который, согласно предельному признаку
Д’Аламбера, сходится. Действительно:![]()
![]()
Поэтому, согласно признаку сравнения, полученный знакоположительный ряд также сходится, а значит, заданный ряд является абсолютно сходящимся.
3)
Чтобы установить, сходится ли заданный
ряд абсолютно, исследуем знакоположительный
ряд
![]() составленный из абсолютных величин
членов данного ряда. Используем
интегральный критерий:
составленный из абсолютных величин
членов данного ряда. Используем
интегральный критерий:
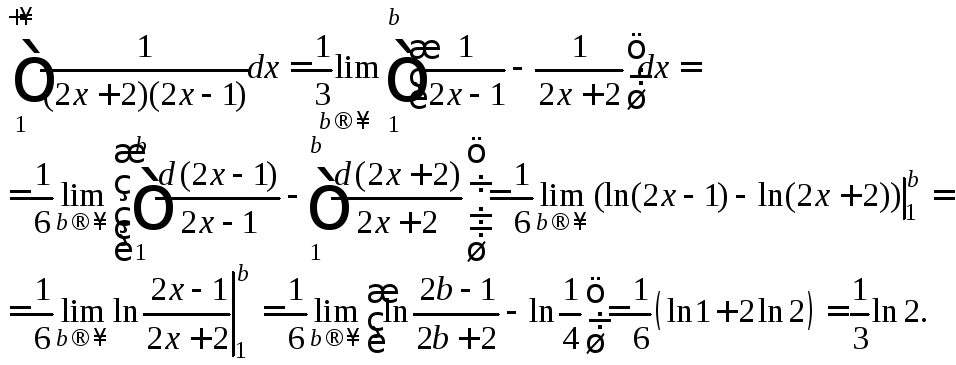
Следовательно, заданный знакочередующийся ряд является абсолютно сходящимся.
4) Для заданного знакопеременного ряда не выполняется необходимый признак сходимости:
![]() –не
существует (
–не
существует (![]() «колеблется» между –1 и 1, не стремясь
ни к какому определенному числу).
Следовательно, заданный знакопеременный
ряд расходится.
«колеблется» между –1 и 1, не стремясь
ни к какому определенному числу).
Следовательно, заданный знакопеременный
ряд расходится.
Пример
2. Установить
сходимость ряда
![]() и вычислить приближенное значение его
суммы с точностью до 0,01.
и вычислить приближенное значение его
суммы с точностью до 0,01.
Решение.
Поскольку члены данного знакочередующегося
ряда убывают по абсолютному значению,
стремясь к нулю:
![]() и
и![]() то согласно признаку Лейбница заданный
ряд сходится. Чтобы обеспечить точность
в 0,01, нужно вычислить несколько
последовательных первых членов ряда,
пока не получим такой член, абсолютное
значение которого меньше
то согласно признаку Лейбница заданный
ряд сходится. Чтобы обеспечить точность
в 0,01, нужно вычислить несколько
последовательных первых членов ряда,
пока не получим такой член, абсолютное
значение которого меньше![]()
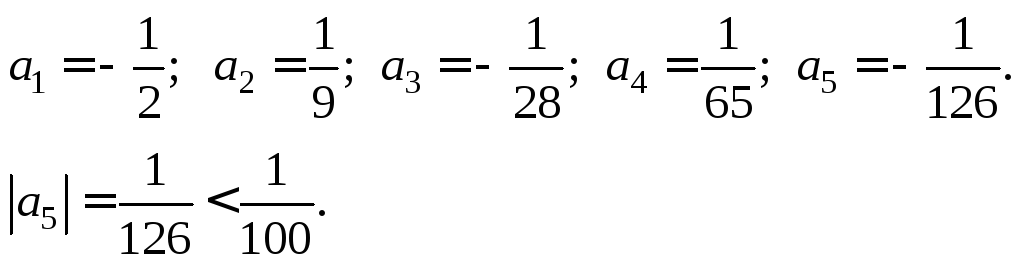
Следовательно, чтобы обеспечить точность до 0,01, нужно взять четыре члена ряда:
![]()
