3.7. Индукция
Закон Фарадея о магнитной индукции гласит, что индуцированное напряжение или электродвижущая сила (э.д.с.) в контуре численно равна и противоположна по знаку скорости изменения магнитного потока Фв, сквозь поверхность ограниченную этим контуром, т.е.
(3.35)
(3.36)
где N — число витков. Это уравнение можно переписать в виде:
(3.37)
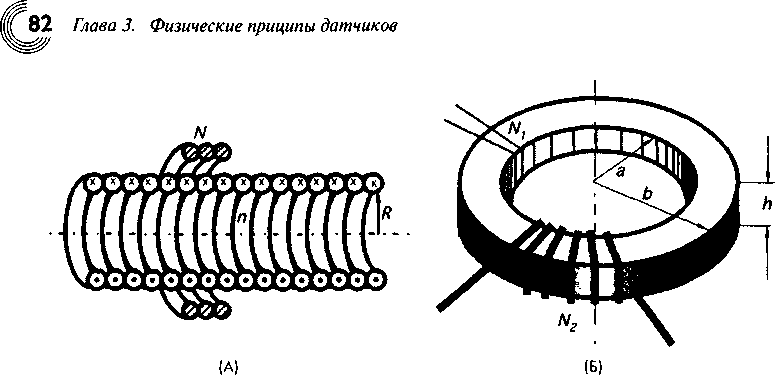
Рис. 3.15 Определение взаимной индуктивности: А — в соленоиде, Б — в тороиде
3.8. Сопротивление
В любых материалах
движение электронов напоминает поведение
газа в закрытом сосуде. Их общие черты:
произвольное направление перемещения
и одинаковая средняя концентрация
электронов в любом месте (считается,
что материал имеет однородную структуру).
Рассмотрим стержень из произвольного
материала длиной 
.
При подключении концов стержня к
источнику напряжения V(рис.
3.16) внутри материала появится электрическое
поле с напряженностью Е:
(3.49)
Скорость потока электрических зарядов (количество зарядов в единицу времени) через поперечное сечение стержня называется электрическим током:
(3.50)
3.9 Удельное сопротивление
Если изготовить два геометрически идентичных стержня из разных материалов (например, из меди и стекла) и приложить к ним равное напряжение, ток, протекающий по ним, не будет одинаковым. Для каждого материала есть характеристика, описывающая его способность пропускать электрический ток. Она называется удельным сопротивлением. При этом говорят, что материал обладает электрическим сопротивлением, которое можно определить по закону Ома:
(3.51)
Для чисто резистивных элементов (не обладающих ни емкостью, ни индуктивностью) напряжение и ток совпадают по фазе.
Сопротивление является характеристикой любого устройства. Его величина определяется как самим материалом, так и геометрией резистора. Материал, как правило, характеризуется величиной удельного сопротивления ρ:
(3.52)
где j — плотность тока: j=i/a (a — площадь поперечного сечения материала).
Удельное сопротивление материала можно выразить через среднее время между столкновениями электронов с атомами вещества τ, заряд электрона е, его массу т и число электронов проводимости в единичном объеме п:
(3.53)
3.10 Температурная чувствительность
Проводимость материала зависит от изменений температуры t, и в сравнительно узком диапазоне она может быть выражена при помощи температурного коэффициента сопротивления (ТКС) α:
(3.55)
3.11 Тензочувствительность
Обычно при механической деформации материала его электрическое сопротивление изменяется. Это явление называется пьезорезистивньш эффектом. С одной стороны, в некоторых случаях этот эффект является причиной возникновения погрешностей. С другой стороны, на его основе можно реализовать тензодатчики, реагирующие на механическое напряжение σ.
(3.60)
где Е— модуль Юнга материала, a F— приложенная сила. В этом уравнении отношение dl/l = e называется относительной деформацией материала.
На рис. 3.19 показан цилиндрический проводник (провод), растянутый при помощи силы F. Объем провода v остается постоянным, тогда как его длина увеличивается, а площадь поперечного сечения уменьшается. В результате уравнение (3.54) может быть переписано в виде:
(3.61)
После дифференцирования получим выражение для определения чувствительности сопротивления к удлинению провода:
(3.62)
Из этого выражения можно сделать вывод, что чувствительность повышается при увеличении длины провода и его удельного сопротивления, а также при уменьшении поперечного сечения. Относительное изменение сопротивления провода является линейной функцией от деформации е и может быть выражено в виде:
(3.63)
где Se — коэффициент тензочувствителъности или чувствительность тензоэлемента. Для металлических проводов он лежит в пределах 2...6, а для полупроводников — 40...200.
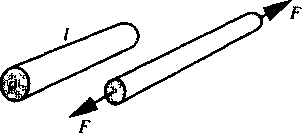
Рис. 3.19 Механическое напряжение приводит к изменению геометрии проводника и его сопротивления