Шпоры / Шпоры по сопромату по 20 тем / Чистый сдвиг

3.3. Чистый сдвиг

Рассмотрим частный случай плоского напряженного состояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку (рис. 3.5,а).

Т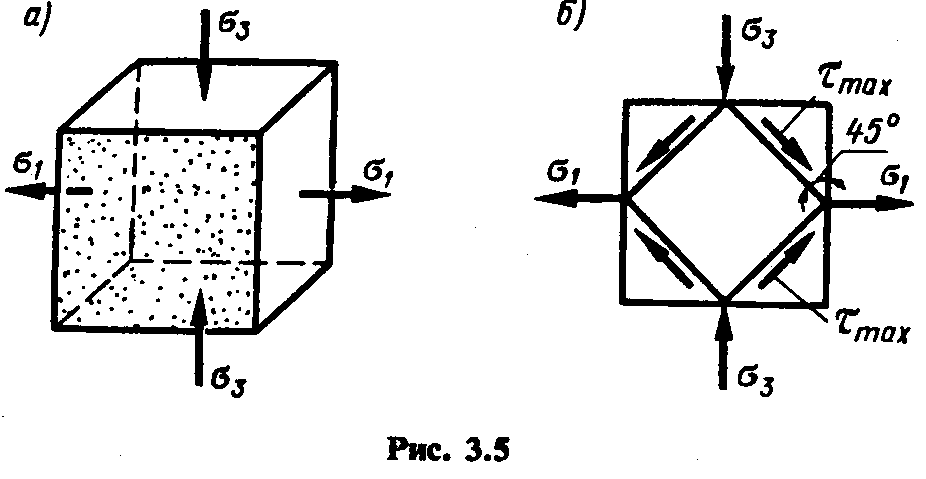вое напряженное состояние носит название чистого сдвига (происхождение этого названия разъяснено несколько ниже). Максимальное главное напряжение следует обозначить о минимальное, а по условию промежуточное главное напряжение = О.

На рис. 3.5,б показана проекция элемента на плоскость, совпадающую с нулевой главной площадкой (отмечена на рис. 3.5,а точками). Для серии площадок, перпендикулярных плоскости чертежа, на основании формул. (3.2), (3.3) и условия имеем;

Максимальное для исследуемой серии площадок касательное напряжение определим, положив в формуле (3.5) . Это напряжение максимально для данной точки тела, а не только для исследуемой серии площадок, так как эти площадки параллельны вектору а~ (см. с. 98 и 99).

Итак, при чистом сдвиге

т|з=т =а, = аз. (3.6)

Подставив в формулу (3.4) а=45' (или и=135'), обнаружим, что т. е. на площадках действия максимальных касательных напряжений нормальные напряжения отсутствуют; эти площадки показаны на рис. 3.5,б.

Чистый сдвиг — единственный случай плоского напряженного состояния, когда через точку можно провести две взаимно перпендикулярные площадки, на которых касательные напряжения максимальны, а нормальные напряжения отсутствуют.

Итак, наряду с определением чистый сдвиг — это частный случай плоского напряженного состояния, при котором не равные нулю главные напряжения равны по значению и противоположны по знаку,—

возможно и другое определение, вытекающее из проведенного исследования:

чистым сдвигом называют такое плоское напряженное состояние, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четырех его гранях были только равные между собой касательные напряженна.

Это последнее определение можно рассматривать как объяснение названия, принятого для данного напряженного состояния.

В качестве примера, иллюстрирующего возникновение чистого сдвига, рассмотрим кручение тонкостенной трубы (рис. 3.6, а). Из условия равновесия отсеченной части трубы, изображенной отдельно на рис. 3.6,6, следует, что в поперечном сечении (любом) возникает лишь один внутренний силовой фактор — крутящий момент М численно равный внешнему моменту М. В поперечном сечении трубы возникают касательные напряжения, так как только касательные силы дают момент относительно продольной оси z бруса. Без большой погрешности, учитывая тонкостенность трубы, можно принять, что по толщине стенки напряжения распределены равномерно. Совершенно очевидно, что все точки трубы, расположенные на любой прямой, параллельной оси z, находятся в одинаковых условиях. Таким образом, во всех точках трубы напряженное состояние одинаково — однородное напряженное состояние. Это обстоятельство повышает надежность и точность экспериментального исследования, поэтому опытное изучение чистого сдвига проводят путем испытания на кручение тонкостенных трубчатых образцов.

Убедимся, что напряженное состояние в любой точке трубы — действительно чистый сдвиг.

Двумя поперечными сечениями, отстоящими друг от друга на расстоянии dz, и двумя радиальными сечениями, угол между которыми дф, вырежем из стенки трубы бесконечно малый элемент (рис. 3.6,а). Он изображен отдельно на рис. 3.7,а. В силу бесконечной малости элемента можно рассматривать его как прямоугольный параллелепипед с ребрами, равными dz, Ь и (D/2)dф. На площадках, соответствующих поперечным сечениям, как было установлено, возникают касательные напряжения т. Соответствующие им внутренние силы образуют пару. Если предположить, что возникают только эти напряжения, равновесие элемента не будет обеспечено, следовательно, на гранях параллелепипеда, совпадающих с продольными (радиальными) сечениями трубы, также должны возникнуть внутренние касательные силы (напряжения т'). Они образуют пару, момент которой уравновешивает момент сил, возникших по площадкам поперечных сечений (рис. 3.7, б). Остальные две грани элемента от напряжений свободны, так как они принадлежат наружной и внутренней поверхностям трубы, к которым никаких сил не приложено. Итак, на четырех гранях выделенного элемента есть только касательные напряжения, а две грани от напряжений свободны, что соответствует второму определению понятия «чистый сдвиг».

Составим уравнение равновесия сил, действующих на выделенный элемент, учитывая, что напряжения т действуют на площади 6-0,50 , а напряжения — на площади Ь dz и плечи соответствующих пар сил равны dz и 0,50дф:

откуда

Этот результат не содержит ничего нового: составив и решив уравнение равновесия, мы просто иначе, чем ранее, доказали закон парности касательных напряжений. Достоинство этого доказательства состоит в том, что при рассмотрении условия равновесия элемента становится особенно ясным, что парные касательные напряжения направлены оба одновременно либо к ребру, либо от ребра пересечения площадок, на которых они возникают.

Рассмотрим теперь вопрос о деформации сдвига. Изобразим элемент, выделенный площадками, на которых возникают только касательные напряжения, в проекции на плоскость, параллельную свободной от напряжений грани (рис. 3.8). Учитывая, что нас интересуют деформации элемента, а не его перемещения как твердого тела, будем считать одну из граней неподвижной. В . результате деформации элемент примет форму, показанную на рис. 3.8 штриховыми линиями. Мерой деформации сдвига служит изменение первоначального прямого угла между гранями элемента, называемое углом сдвига и обозначаемое у. Угол сдвига выражается в радианах.

В известных пределах, зависящих от свойств материала, между углом сдвига и соответствующим касательным напряжением существует прямая пропорциональность — закон Гука при сдвиге. Математическая запись этого закона имеет вид

Здесь G — упругая постоянная материала, характеризующая его жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости 2-ro рода. Очевидно, размерность модуля сдвига та же, что и напряжения.

Можно доказать, что для изотропного тела между тремя упругими постоянными — модулем продольной упругости Е, коэффициентом Пуассона и модулем сдвига G — существует следующая зависимость:

Как известно, значение коэффициента Пуассона лежит в пределах . Следовательно, модуль сдвига составляет 0,33...0,5 от модуля продольной упругости. Для многих металлов и сплавов, в частности для стали, ; в среднем для стали

Удельная энергия деформации при чистом сдвиге определяется по формуле

аналогичной выражению (2.20), определяющему удельную энергию деформации при одноосном (линейном) напряженном состоянии.