
ПСОД студенты / Корреляционный анализ
.pdf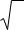
Проверка на однородность случайных ошибок
Для проверки на однородность дисперсии D(ε)=const. Целесообразно воспользоваться методом Гольфельда. Последовательность значений случайной величины Y разбивается на две последовательности объемом n1 и n2 , где (n1+n2=n). Для каждой последовательности вычисляются дисперсии
воспроизводимости S12 и S22 . Тогда отношение
F = S2
2 ,
S2
1
при S12 < S22 будет иметь распределение Фишера со степенями свободы
f1= n1 − k −1 ; f2= n2 − k −1 . Если значение F превышает табличное, то гипотеза об однородности дисперсии отклоняется. Чувствительность критерия увеличивается, если исключить средние наблюдения.
В случае, если дисперсии оказались неоднородными, часто оказывается полезным изменение масштаба для выходной переменной. Вводится
некоторая функция от выходной переменной, например ln y или y.
Проверка на автокорреляцию случайных ошибок
Наличие автокорреляции ошибок можно проверить с помощью критерия Дарбина-Уотсона:
|
n |
|
|
DW = |
∑(ei −ei−1)2 |
. |
|
i=2 |
|
||
|
n |
||
|
|
∑ei2 |
|
|
|
i=1 |
|
Критерий Дарбина-Уотсона изменяется в диапазоне 0 ≤ DW ≤ 4. При отсутствии автокорреляции DW=2. В приложении 3 приводятся нижние и верхние границы критерия dн и dвдля степеней свободы f1=n; f2=k.
Если |
≤ DW ≤ dн, есть положительная автокорреляция, |
||
0 |
|||
4–dн ≤ DW ≤ 4, |
есть отрицательная автокорреляция, |
||
dв |
≤ DW ≤ 4–dв, |
автокорреляция отсутствует, |
|
|
dн |
< DW < dв или 4–dв ≤ DW ≤ 4–dн, нужны дополнительные |
|
исследования.

П р а к т и ч е с к и й с о в е т: желательно область неопределенности подключить к области отклонения гипотезы об отсутствии автокорреляции.
2.6.ОПИСАНИЕ ТИПОВОГО ПРИМЕРА
Втабл. 2.2 приведены значения выходной переменной yi при данном значении входной переменной xi . Модель ищется в виде
~y = a0 +a1 x .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|||
Y |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
7 |
|||
1. Вычислим оценки |
математических |
|
ожиданий, смещенные и |
|||||||||||||||||||||||||||||||||
несмещенные оценки дисперсий и средних квадратических отклонений: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
1 |
∑xi = 2,5 , |
|
|
= |
1 |
∑yi = 4,5 , |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x |
y |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
n |
|
||||||||||||||||||||||||||
Sх2 |
= |
|
1 |
∑(xi − |
|
)2 |
=1,250 , |
Sy2 |
= |
1 |
|
∑( yi − |
|
|
)2 |
= 3,251, |
||||||||||||||||||||
|
x |
y |
||||||||||||||||||||||||||||||||||
|
|
|
n |
|||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Sхн2 |
|
1 |
|
|
∑(xi − |
|
)2 =1,666 , |
|
Sy2н |
|
|
1 |
∑( yi − |
|
)2 |
|
||||||||||||||||||||
= |
|
|
x |
|
= |
|
|
|
= 4,333, |
|||||||||||||||||||||||||||
|
|
|
y |
|||||||||||||||||||||||||||||||||
n − |
1 |
|
|
n |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sх |
= |
1 |
∑(xi − x)2 |
=1,118 |
, |
Sy |
= |
|
|
|
1 |
∑( yi − y)2 |
=1,803, |
|||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
Sхн = |
1 |
|
|
∑(xi − x)2 =1,291 |
, |
Syн |
= |
|
|
|
|
1 |
∑( yi − y)2 = 2,082 . |
|||||||||||||||||||||||
|
|
n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n −1 |
|
|
|
|
|
|
|
|||||||
2. Определим модель. Вычислим соответствующие суммы и составим систему двух линейных уравнений:
Σxi=10, Σyi=18, Σxi2=30, Σxiyi=53, Σyi2=94,

|
|
a0 |
+ 10 |
a1 |
=18 , |
|||
4 |
|
|
|
a1 |
||||
|
|
|
a0 |
+30 |
= 53, |
|||
10 |
|
|
|
|||||
решая которую, получаем: |
|
|
a0 = 0,5, a1 =1,6. Модель имеет вид |
|||||
|
~ |
= 0,5 +1,6x |
||||||
|
y |
|||||||
3. Рассчитаем модельные значения, подставляя в уравнение значения входной переменной (табл. 2.3).
|
|
|
|
|
|
|
|
|
Таблица 2.3 |
|
|
~ |
|
2,1 |
|
3,7 |
|
5,3 |
|
6,9 |
|
|
|
|
|
|
|
|||||
|
y |
|
|
|
|
|
||||
4. Определим адекватность модели, для этого вычислим общую сумму квадратов, сумму квадратов, относящуюся к регрессии, и сумму квадратов остатков:
Q = ∑( y |
− |
|
)2 = ∑ y2 − |
(∑ y)2 |
=94 − |
(18)2 |
|
=13 |
|
|||||||||||
y |
; |
|||||||||||||||||||
|
|
|||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
~ |
|
|
|
|
|
2 |
|
~2 |
|
(∑ y)2 |
|
|
(18)2 |
|
|
|
||||
|
|
|
y ) |
|
|
|
|
|
|
|
||||||||||
Q R = ∑ ( y i − |
|
|
= |
∑ y |
− |
|
|
= 93,8 − |
|
|
|
=12,8 ; |
||||||||
|
|
n |
|
4 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Qe=Σei2=(2–2,1)2+(4–3,7)2+(5–5,3)2+(7–6,9)2=0,2 .
Для проверки полученных расчетов необходимо, чтобы Q =QR +Qe .
В нашем случае равенство выполняется. Расчетное значение критерия Фишера равно
F = |
|
QR / k |
|
= |
S2R |
= |
12,8 /1 |
=128. |
|
Qe |
/(n −k |
−1) |
S2 |
0,2 /(4 −1−1) |
|||||
|
|
|
|
Расчетное значение критерия Фишера больше, чем табличное значение
F > FТАБЛ.=F0,05;1;2=18,512.
Вывод 1: модель адекватна, исходные данные хорошо согласуются с моделью.
5. Оперативно адекватность модели можно проверить по коэффициентам детерминации или корреляции. Коэффициент
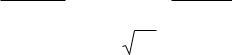
детерминации, скорректированный коэффициент детерминации и коэффициент корреляции определяются следующим образом:
R2 = |
Q R |
= |
Q R = |
12,8 |
= 0,9846 , |
|
Q R + Q e |
|
|
||||
|
|
Q |
13 |
|
||
R*2 =1− n −n −k 1−1(1−R2) =1− 44−−1−11(1−0,9846) =0,977,
R = R2 = 0,9922 .
Полученное значение коэффициента детерминации больше, чем 0,75 следовательно, модель можно считать адекватной.
6. Определим значимость параметров модели. Вычислим средние квадратические отклонения ошибок коэффициентов регрессии:
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
S2 ∑xi2 |
|
|
0,1 30 |
|
|||
2 |
2 |
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
Sa0 |
=S |
( |
|
+ |
|
|
|
|
|
|
|
|
) |
|
= |
|
|
|
|
= |
|
|
|
=0,15; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 30−(10)2 |
||||||||||||
n |
∑(xi −x)2 |
|
n∑xi2 −(∑xi)2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Sa2 |
= |
|
|
s2 |
|
|
|
= |
|
|
|
|
nS2 |
= |
|
4 0,1 |
|
=0,02; |
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|||||||
|
|
1 |
|
|
∑(xi −x) |
|
|
|
|
|
|
2 |
|
4 30−(10) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
n∑xi |
−(∑xi) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
S a 0 |
= 0,387 ; |
S a 1 |
= |
0 ,141 . |
|
|
|
|||||||||||||
Табличное значение Стьюдента t2;0,025=4,303. Получаем расчетные значения Стьюдентов:
ta0 =0,5/0,387=1,291; ta1 =1,6/0,141=11,31.
Вывод 2: параметр a1 будет значим так, расчетное значение Стьюдента
будет больше, чем табличное, параметр a0 – незначим.
Аналогичный вывод можно сделать иначе, вычисляя доверительные интервалы для параметров модели:
a0 =0,5±4,303·0,387=0,5±1,665; a1 = 1,6±4,303·0,141= 1,6±0,607.

Так как абсолютное значение параметра a1 будет больше, чем его доверительный интервал, то параметр значим. Параметр a0 незначим.
7. Оценка |
среднеквадратического |
отклонения |
ошибки |
S = S2 = 0,1 =0,316. Разделив все отклонения (остатки) |
на эту |
||
величину, получим нормированные отклонения, которые все находятся в интервале [-2; +2].
Вывод 3: первая предпосылка выполняется, случайная ошибка имеет нормальный закон распределения с нулевым математическим ожиданием.
8. Критерий Дарбина-Уотсона вычисляем следующим образом:
DW = ((0,3+0,1)2+(–0,3–0,3)2+(0,1+0,3)2) / 0,2=3,4
1,5 < DW < 4–1,5 (dв примерно равно 1,5 (прил. 3)).
Вывод 4: вторая предпосылка не выполняется, между текущими значениями случайной величины присутствует отрицательная автокорреляция.
В завершении работы приведем итоговую таблицу остатков и нормированных отклонений (табл. 2.4).
|
|
|
|
Таблица 2.4 |
|
|
|
|
|
|
|
N/N |
Значение Y |
Оценка Y |
Остатки |
Нормированные |
|
|
|
|
|
отклонения |
|
1 |
2 |
2,1 |
–0,1 |
–0,316 |
|
2 |
4 |
3,7 |
0,3 |
0,948 |
|
3 |
5 |
5,3 |
–0,3 |
–0,948 |
|
4 |
7 |
6,9 |
0,1 |
0,316 |
|
2.7. STATISTICA. |
ПРОВЕРКА |
РЕЗУЛЬТАТОВ КОНТРОЛЬНОГО |
|
ПРИМЕРА MULTIPLE REGRESSIN |
|
||
Для проведения расчетов с модулем предварительной обработки |
|||
необходимо выполнить следующие действия: |
|
||
• запустить |
программу |
STATISTICA |
командой |
Пуск/Программы/Statistica/Statistica;
•выделить строку Basic Statistica/Tables и нажать кнопку Switch To;
•в открывшемся окне Basic Statistica/Tables закрыть все окна документов и выполнить команду File/New Data. Появится таблица для ввода данных (рис. 2.1);

Рис. 2.1
•введите исходные данные для переменных X и Y в столбцы VAR1 и
VAR2;
•выделите блок колонок VAR3-VAR10 и нажмите на панели инструментов кнопку Vars. В появившемся меню выберите команду Delete, а затем в диалоговом окне нажмите кнопку OK;
•выделите блок строк 5–10 и нажмите на панели инструментов кнопку Cases. В появившемся меню выберите команду Delete, а затем в диалоговом окне нажмите кнопку OK;
•щелкните правой клавишей мыши по столбцу VAR1 и выберите команду Variable Specs.... (Спецификации переменной). Появится диалоговое окно (рис. 2.2).
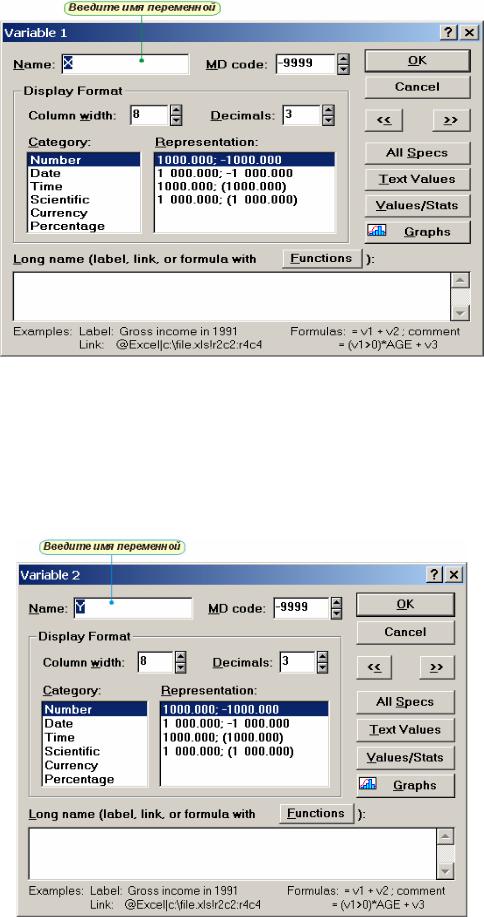
Рис. 2.2
•введите имя переменной X и нажмите OK;
•щелкните правой клавишей мыши по столбцу VAR2 и выберите команду Variable Specs.... (Спецификации переменной). Появится диалоговое окно (рис. 2.3);
Рис. 2.3

•введите имя переменной Y и нажмите OK;
•в результате вы должны получить таблицу данных следующего вида
(рис. 2.4);
Рис. 2.4
•сохраните полученный файл данных командой File/Save As под именем lab1.sta в предназначенной для работы папке;
•сделайте активным окно с таблицей данных, а затем выполните команду Analysis/Resume Analysis (Анализ/Резюме анализ). Появится окно
(рис. 2.5);
Рис. 2.5
• выберете пункт Descriptive statistics (Описательные статистики) и
нажмите OK. Появится окно (рис. 2.6);
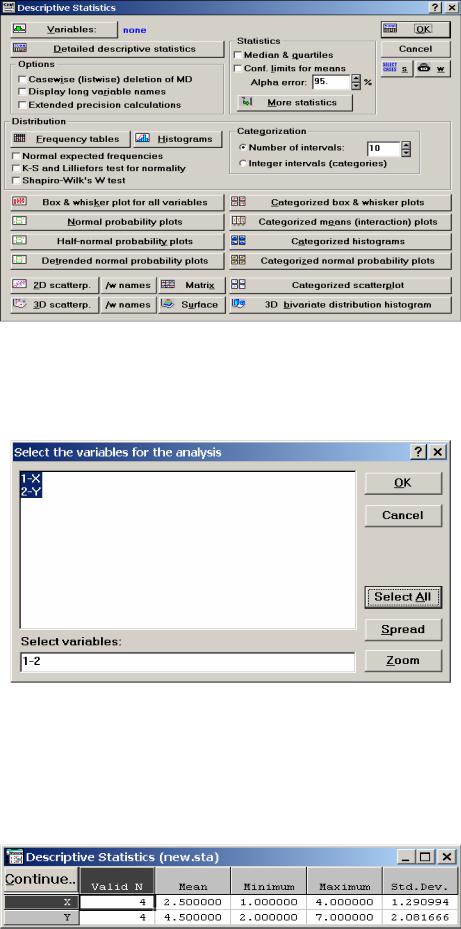
Рис. 2.6
• нажмите кнопку Variables. В появившемся (рис. 2.7) диалоговом окне нажмите кнопку Select All (Выбрать все) и OK;
Рис. 2.7
• программа выполнит переход в предыдущее окно, в котором необходимо нажать кнопку Detailed descriptive tatistics (Детальные описательные статистики). Появится таблица с результатами расчетов (рис. 2.8);
Рис. 2.8
•выпишите необходимые данные – Mean (Выборочное среднее), Std.Dev. (Стандартная девиация-среднее квадратическое отклонение);
•нажмите кнопку Continue. Выполнится переход в предыдущее окно, нажмите кнопку 2D scatterp. Появится окно для выбора переменных (рис. 2.9);
Рис. 2.9
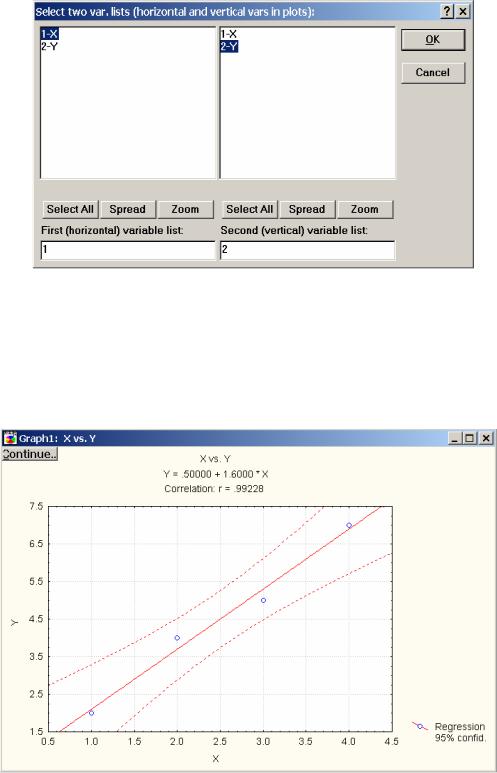
•сделайте необходимые изменения и нажмите кнопку OK;
•появится окно (рис. 2.10) с графиком линейной регрессионной модели, с рассчитанными значениями коэффициентов модели и коэффициентом корреляции. Первая часть работы выполнена.
Рис. 2.10
