4. Взаимно однозначные соответствия

В математике изучают различные виды соответствий. Это не случайно, поскольку взаимосвязи, существующие в окружающем нас мире многообразны. Для учителя, обучающего математике младших школьников, особую значимость имеют взаимно однозначные соответствия.

Определение. Взаимно однозначным соответствием между множествами Х и У называется такое соответствие, при котором каждому элементу множества Х сопоставляется единственный элемент множества У и каждый элемент множества У соответствует только одному элементу множества Х.

Рассмотрим примеры взаимно однозначных соответствий.

Пусть Х – множество кругов, У – множество квадратов и соответствие между ними задано при помощи стрелок.

Это соответствие взаимно однозначное, так как каждому кружку из множества Х сопоставляется единственный квадрат из множества У и каждый квадрат из У соответствует только одному кружку из множества Х.

Пример

Пусть Х – множество действительных чисел, У – множество точек координатной прямой. Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Это соответствие взаимно однозначное, так как каждому действительному числу сопоставляется единственная точка координатной прямой и каждая точка на прямой соответствует только одному числу.

В математике взаимно однозначное соответствие между множествами Х и У часто называют взаимно однозначным отображением множества Х на множество У.

5. Равномощные множества

Определение. Множества Х и У называются равномощными, если между ними можно установить взаимно однозначное соответствие.

Если множества Х и У равномощны, то пишут Х  У.

Нетрудно видеть, что множества рассмотренные в предыдущих примерах равномощны.

Равномощными могут быть как конечные, так и бесконечные множества Равномощные конечные множества называют еще равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие. Например, пишут, что 5 = 5, так как кружков столько же, сколько квадратов.

Понятие равночисленности множеств лежит и в основе определения отношений «больше на …» и «меньше на…» . Например, чтобы утверждать, что 6 больше 4 на 2, сравнивают два множества, устанавливая взаимно однозначное соответствие между множеством Х, в котором 4 элемента, и подмножеством У₁ другого множества У, в котором 6 элементов, и делают вывод: треугольников столько же, сколько кружков, и еще 2. Другими словами, треугольников на 2 больше, чем кружков.

Х

У₁

У

Как уже было сказано, равномощными могут быть и бесконечные множества.

Пример

Пусть Х – множество точек отрезка АВ, У – множество точек отрезка СD, причем длины отрезков различны. Так как между данными множествами можно установить взаимно однозначное соответствие, то множества точек АВ и СD равномощны.

N

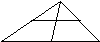
A M B

С M’ D

Пример

Рассмотрим множество N натуральных чисел и множество У – четных натуральных чисел. Они равномощны, так как между их элементами можно установить взаимно однозначное соответствие:

N: 1 2 3 … п …

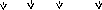
У: 2 4 6 … 2п …

Замечание. На первый взгляд кажется парадоксальным тот факт, что можно установить взаимно однозначные соответствия между множеством и его частью: для конечных множеств такая ситуация невозможна. Однако в математике доказано, что для бесконечного множества А всегда найдется такое его подмножество В, что между А и В можно установить взаимно однозначное соответствие. Иногда это утверждение считают определением бесконечного множества.

Определение. Если бесконечное множество равномощно множеству N натуральных чисел, его считают счетным.

Любое бесконечное подмножество множества N счетно: чтобы пронумеровать его элементы, надо расположить элементы подмножества в порядке возрастание и нумеровать один за другим. Так, счетно множество всех нечетных натуральных чисел, множество натуральных чисел, кратных 5 и др. Счетными являются также множества всех целых чисел, всех рациональных.

Существуют ли множества, отличные от счетных? Доказано, что бесконечным множеством, не равномощным множеству N натуральных чисел, является множество R всех действительных чисел.