
- •Завдання для самостійної роботи
- •1. Вивчити основні властивості (алгебраїчність, асоціативність, комутативність, існування нейтрального елемента, наявність оборотних елементів) дії над елементами множини , якщо:
- •4. Знайти порядок елемента групи . Побудувати циклічну групу, породжену цим елементом та виписати усі її підгрупи:
- •5. Перевірити, чи утворює кільце щодо звичайних дій додавання та множення чисел множина . Якщо відповідь позитивна, то з’ясувати, чи є це кільце полем.
- •6. Перевірити, чи утворює кільце множина . Чи є це кільце полем?
6. Перевірити, чи утворює кільце множина . Чи є це кільце полем?
|
№ варіанта |
|
|
1 |
Множина
|
|
2 |
Множина
|
|
3 |
Множина
|
|
4 |
Множина
|
|
5 |
Множина
|
|
6 |
Множина
|
|
7 |
Множина
|
|
8 |
Множина
|
|
9 |
Множина
многочленів довільного невід’ємного цілого степеня з цілими коефіцієнтами відносно звичайних дій додавання та множення многочленів. |
|
10 |
Множина
|
|
11 |
Множина
|
|
12 |
Множина
|
|
13 |
Множина
|
|
14 |
Множина
|
|
15 |
Множина
|
|
16 |
Множина
|
|
17 |
Множина
|
|
18 |
Множина
|
|
19 |
Множина
|
|
20 |
Множина
|

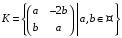 відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. матриць другого порядку з цілими
елементами відносно звичайних дій
додавання та множення матриць.
матриць другого порядку з цілими
елементами відносно звичайних дій
додавання та множення матриць. матриць другого порядку з раціональними
елементами відносно звичайних дій
додавання та множення матриць.
матриць другого порядку з раціональними
елементами відносно звичайних дій
додавання та множення матриць. векторів простору щодо дій додавання
та векторного множення векторів.
векторів простору щодо дій додавання
та векторного множення векторів. цілочисельних векторів простору щодо
дій додавання та векторного множення
векторів.
цілочисельних векторів простору щодо
дій додавання та векторного множення
векторів. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць.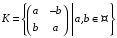 відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць.
 відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. многочленів довільного невід’ємного
цілого степеня з раціональними
коефіцієнтами відносно звичайних
дій додавання та множення многочленів.
многочленів довільного невід’ємного
цілого степеня з раціональними
коефіцієнтами відносно звичайних
дій додавання та множення многочленів. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. всіх можливих дробово-раціональних
функцій з дійсними коефіцієнтами (
всіх можливих дробово-раціональних
функцій з дійсними коефіцієнтами ( – мнгочлени довільного степеня від
змінної
– мнгочлени довільного степеня від
змінної
 з з дійсними коефіцієнтами) відносно
звичайних дій додавання та множення
таких функцій.
з з дійсними коефіцієнтами) відносно
звичайних дій додавання та множення
таких функцій.
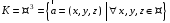 векторів з раціональними координатами
щодо дій додавання та векторного
множення векторів.
векторів з раціональними координатами
щодо дій додавання та векторного
множення векторів. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць.