
Теорія цифрового зображення (Лекції 1-3)
.pdf
таким, що не вносить зміни |
значення яскравості. Якщо |
|
, |
|
і |
||
, перетворення перетворюється |
на порогову |
ункцію, |
яка в |
||||
результаті продукує |
бінарне |
зображення, |
як це показано |
= |
|
= 0 |
|
на рис. 3.2(б). |
|||||||
= − 1 |
) і |
|
|
|
|
|
|
Проміжні значення |
забезпечують різні степені розтягування |
||||||
рівнів яскравості на(результуючому, ( , ) |
зображенні, змінюючи тим самим його |
контраст. |
|
Рис. 3.10. Посилення контрасту. (а) вигляд функції перетворення; (б) початкове малоконтрастне зображення; (в) результат посилення контрасту;
(г) результат порогового перетворення
На рис. 3.10( ) представлено початкове малоконтрастне 8-бітове |
||||||||
відповідно, мінімальна( , ) |
=та( |
,0) ( , |
) = ( |
,, |
− 1) |
|
|
|
зображення. На |
3.10(в) |
показаний |
результат |
посилення контрасту, |
||||
отриманий при |
|
і |
|
|
|
де |
і |
, |
|
максимальна |
яскравості |
на |
зображенні |
Т |
|
||
чином, функції перетворення лінійно розтягує початковий діапазон
яскравості в повний діапазон |
|
|
. Нарешті, на рис. 3.10(г) показаний |
||||
результат порогового |
перетворення |
1] |
|
де |
- середнє значення |
||
|
[0, |
|
|
|
|
||
яскравості на зображенні. В якості |
початкового зображення в цьому прикладі |
||||||
|
= |
= , |
|
|
|||
використаний знімок квіткового пилку, отриманий скануючим електронним мікроскопом зі збільшенням в 700 разів.
2.4.2. Вирізання діапазону яскравості
Часто буває бажано виділити якийсь конкретний діапазон яскравості на зображенні. У практичних застосуваннях може знадобитися покращення

контрасту окремих деталей, таких як ділянки води на супутникових зображеннях або дефектів виробів на рентгенівських знімках. Існують різні способи вирізання рівнів яскравості, проте більшість з них є варіаціями двох наступних підходів. Перший підхід полягає у відображенні усіх тих рівнів, які представляють інтерес, деякою однією високою яскравістю, а усіх інших рівнів - іншою (низькою). Таке перетворення, показане функцією на рис. 3.11(а), дає в результаті бінарне зображення. Другий підхід, ґрунтований на перетворенні з функцією на рис. 3.11(б), підвищує яскравість точок з вибраного діапазону, але зберігає яскравості фону і інших точок зображення. На рис. 3.11(в) представлено початкове півтонове зображення, а на рис. 3.11(г) - результат перетворення, що використовує функцію з рис. 3.11(а).
Рис. 3.11. (а) Дане перетворення виділяє діапазон яскравостей [А, В] і приводить інші значення до рівня константи; (б) дане перетворення виділяє діапазон яскравостей [А, В], але зберігає усі інші рівні; (в) початкове півтонове зображення; (г) результат перетворення з використанням функції
(а).
2.4.3.Вирізання бітових площин
Замість виділення діапазонів яскравості, може виявитися корисним виділення інформації про вклад тих або інших бітів в загальне зображення. Нехай кожен піксель зображення представлений 8 бітами. В цьому випадку усе зображення можна уявити собі у вигляді восьми бітових площин (рис. 3.12).

Рис. 3.12. Представлення 8-бітового зображення у вигляді набору бітових площин
На Рис. 3.14 представлені усі бітові площини зображення, показаного на Рис. 3.13.
Рис. 3.13. 8-бітове фрактальне зображення
Можна помітити, що старші біти(головним чином перші чотири) містять основну частину візуально значимих даних. Інші бітові площини дають вклад в тонші деталі зображення. Розділення цифрового зображення на бітові площини корисне для аналізу відносної інформативності, яку несе кожен біт зображення, що дозволяє оцінити необхідне число бітів, потрібне для квантування кожного пікселя.
На основі добування бітових площин з 8-бітового зображення неважко показати, що (бінарне) зображення бітової площини 7 може бути отримано обробкою початкового зображення пороговим градаційним перетворенням, яке (1) відображає усі рівні зображення від 0 до 127 в деякий один (наприклад, 0); і (2) відображає усі рівні від 128 до 255 в іншій (наприклад, 255). Бінарне зображення для бітової площини 7 на рис. 3.14 було отримано саме таким чином.

Рис. 3.14. Вісім бітових площин зображення на рис. 3.13. У нижньому правому кутку кожного зображення нанесений номер, що ідентифікує бітову площину
3. Видозмінення гістограми |
( ) = |
|
|
||
[0, – 1] |
|
|
|
|
|
Гістограмою цифрового зображення з рівнями яскравості в діапазоні |
|||||
|
називається дискретна функція |
|
, де |
є –тий рівень |
|
яскравості, а |
- кількість пікселів на зображенні, що мають яскравість |
||||
Загальною практикою є нормалізація гістограми шляхом ділення кожного
значення на загальну кількість пікселів |
( |
зображенні, що позначається |
Тим |
||||||
= 0,1,..., − 1. |
|
|
|
|
|
|
для |
||
самим, |
значеннями нормалізованої |
гістограми будуть |
вiрогідності |
||||||
|
|
Взагалі кажучи, |
|
|
) є оцінкою |
( |
) = |
/ |
|
пікселя |
зі значенням яскравості |
. |
Відмітимо, що |
сума |
усіх |
значень |
|||
нормалізованої гістограми рівна одиниці, видозміна гістограми (обробка гістограми) може бути успішно використана для покращення зображень. Гістограми досить прості як для програмного обчислення, так і для апаратної реалізації, що робить їх зручним інструментом для обробки зображень у реальному часі.
В якості знайомства з місцем гістограми в покращенні зображень, розглянемо рис. 3.15, на якому приведений той самий знімок пилку, що і на рис. 3.10, але показаний тут в чотирьох варіантах яскравісних характеристик: темному, світлому, низькоконтрастному й висококонтрастному. На правій частині рисунка приведені гистограммы, що відповідають цим зображенням.

від |
горизонтальній осі кожного графіку відкладені значення рівнів яскравості |
|||||||
або ( ) = / від |
|
|
|
|
( |
) |
|
|
. |
вертикальній осі - значення гістограми |
|
це залежності |
) |
|
/ |
||
якщо вони нормалізовані). Тим самим, ці |
графіки |
|
||||||
|
( |
) = |
( абор( |
|
||||
Рис. 3.15. Чотири основні типи зображень: темне, світле, низькоконтрастне і висококонтрастне
Легко бачити, що на гістограмі темного зображення ненульові рівні сконцентровані в області низьких (темних) значень діапазону яскравості. Аналогічно, значимі рівні гістограми яскравого зображення зміщені до верхньої частини діапазону. Зображення з низьким контрастом має вузьку гістограму, розташовану поблизу центру діапазону яскравості. Для одноколірного зображення це означає в’ялий сірий вигляд. Нарешті видно, що ненульові рівні гістограми висококонтрастного зображення покривають

широку частину діапазону яскравості, а також, що розподіл значень пікселів не занадто відрізняється від рівномірного, за винятком невеликої кількості піків, що височіють над іншими значеннями. Інтуїтивно можна зробити висновок, що зображення, розподіл значень елементів якого близький до рівномірного і займає увесь діапазон можливих значень яскравості, виглядатиме висококонтрастним і міститиме велику кількість півтонів.
|
3.1. Еквалізація гістограми |
|
|
|
|
|
|
|||||||
|
Для простоти спочатку розглянемо неперервні функції. Передбачається, |
|||||||||||||
що |
значення |
що |
відображають |
яскравість |
елементів зображення, |
|||||||||
розподілені |
неперервно в діапазоні |
[0,1], при |
цьому значення |
|
до |
|||||||||
відповідає чорному, |
|
– білому. Пізніше буде здійснений перехід |
|
0 |
||||||||||
дискретного |
представлення, а інтервал значень буде розширений до |
[ , |
|
− |
||||||||||
|
|
= 1 |
|
|
|
|
|
|
||||||
1]. |
Для будь-якого |
що задовольняє вищезгаданим умовам, розглядається |
||||||||||||
перетворення виду |
= |
( ) 0 ≤ ≤ 1, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
. |
) |
||||
|
яке для будь-якого пікселя, що має значення r, дає значення s. З причин, |
|||||||||||||
які стануть очевидні нижче, ми припускаємо, що функція перетворення |
( |
) |
||||||||||||
задовольняє наступним умовам: |
≤ 1. |
|
|
|
|
|
||||||||
|
(б) |
( |
) |
( ) ≤ 1 при 0 ≤ |
|
|
|
0 ≤ ≤ 1 |
||||||
|
(а) |
|
|
однозначною і монотонно зростаючою на інтервалі |
|
|
|
; |
||||||
|
В умові (а) вимога однозначності функції |
потрібна для існування |
||||||||||||
зворотного перетворення, а вимога монотонності( |
)для збереження порядку |
|||||||||||||
зміни яскравості від чорного до білого на вихідному зображенні. Функція перетворення, яка не є монотонно зростаючою, може призвести до появи на вихідному зображенні інтервалів яскравості з інвертованими значеннями. Нарешті, умова (б) означає, що допустимий діапазон вихідних значень сигналу співпадає з діапазоном вхідних значень. На рис. 3.16 показаний
приклад функції перетворення, яка задовольняє поставленим вище умовам. |
||
( ) |
0 ≤ ≤ 1 |
(3.7) |
Зворотне перетворення з в буде наступним: |
|
|

Рис. 3.16. Однозначна і монотонно зростаюча функція градаційного
перетворення |
|
Рівні яскравості |
зображенні можуть розглядатися як значення |
випадкової величини в інтервалі [0,1]. Однією з найважливіших характеристик випадкової величини являється густина розподілу
ймовірностей. |
Нехай |
і |
- густини розподілу ймовірностей |
|||
випадкових змінних і |
відповідно,( ) ( |
)де індекс при р означає, що |
і |
|||
різними функціями |
елементарної теорії ймовірностей слідує ( ) |
якщо( ) |
||||
і |
відомі й задовольняють умові (а), то густина розподілу |
|||||
ймовірностей( ) ( ) |
значень перетвореного сигналу s може бути отримана за |
|||||
допомогою простої( )формули: ( ) = |
( ) |
|
|
(3.8) |
||
|
|
|||||
Таким чином, густина розподілу ймовірностей значень перетвореного сигналу s задається густиною розподілу ймовірностей значень яскравості
вхідного зображення і обраною функцією перетворення. |
|
||
У обробці зображень особливу важливість має наступна функція: |
|
||
= |
( ) = |
( ) |
(3.9) |
де w - змінна інтегрування. Права частина∫ |
рівняння (3.9) є не що інше, як |
||
функція розподілу випадкової змінної r. Оскільки густина розподілу ймовірностей завжди додатна, а інтеграл функції є площа під графіком функції,отже, ця функція перетворення є однозначно визначеною і монотонно зростаючою, і, тим самим, задовольняє умові (а). Аналогічно, оскільки інтеграл густини розподілу ймовірностей випадкової величини під
час зміни |
в діапазоні [0,1] також знаходиться в діапазоні [0,1], то умова (б) |
||
також виконується. |
), густину розподілу ймовірностей |
||
Знаючи функцію перетворення T |
|||
можна знайти з рівняння (3.8). З диференціального( |
числення відомо, що |
||
похідна( ) |
визначеного інтеграла за |
його верхньою |
межею дорівнює |
підінтегральному виразу в точці верхньої межі (правило Лейбніца). Іншими словам

|
|
= |
|
) |
= |
|
|
|
∫ |
( ) |
= |
( ) |
|
(3.10) |
|||
|
|
|
|
|
|
|
|||||||||||
підставляючи даний результат для |
|
|
у рівняння (3.8), і вважаючи, що |
||||||||||||||
|
|
||||||||||||||||
усі значення густини ймовірностей більше нуля, отримуємо в результаті: |
|||||||||||||||||
( ) = |
( ) |
|
|
|
= |
|
( ) |
) |
= 1 |
0 ≤ |
≤ 1. |
(3.11) |
|||||
|
|
|
|
||||||||||||||
Таким чином, ми отримали, що |
|
|
є рівномірною густиною розподілу |
||||||||||||||
ймовірностей на відрізку |
[0, |
1], |
яка( |
дорівнює) |
нулю |
за межами |
даного |
||||||||||
інтервалу. Просто кажучи, було продемонстровано, що виконання градаційного перетворення згідно функції, що задана рівнянням (3.9), призводить до отримання деякої випадкової величини s, яка характеризується
рівномірною густиною |
зподілу ймовірностей. Тут важливо відмітити, що |
||||
хоча |
як це випливає |
(3.9), залежить від |
, результуюча густина |
||
розподілу( ), |
ймовірностей |
|
, як випливає з (3. ),( |
завжди) |
є рівномірною, |
незалежно від форми |
( ) |
|
|
||
У випадку дискретних( |
значень, замість густини розподілу ймовірностей |
||||
та інтегралів ми маємо справу з ймовірністю конкретних значень і сумами.
Ймовірність появи пікселя із значенням яскравості приблизно дорівнює |
|||||
|
( ) = |
|
= 0,1,2,…, |
− 1 |
(3.12) |
|
|
||||
де n - загальна кількість пікселів на зображенні, |
- кількість точок з |
||||
яскравістю , |
- максимально |
допустима кількість |
рівнів |
яскравості на |
|
зображенні. Дискретним аналогом функції перетворення, що задається рівнянням (3.9), буде
= ( ) = ∑ |
( ) = ∑ |
|
|
= 0,1,2,…, |
−1 (3 13) |
|
|
||||||
Таким чином, оброблене (вихідне) зображення утворюється |
||||||
відображенням кожного пікселя вхідного зображення, що має яскравість |
, у |
|||||
відповідний елемент вихідного зображення зі значенням |
, згідно |
з |
||||
рівнянням (3.13). Як вказувалося раніше, залежність |
від |
називають |
||||
( ,)
гістограмою. Перетворення (відображення), що задається рівнянням(3.13), називається еквалізацією або лінеаризацією гістограми.
Іншими словами, отримуючи на вхід зображення, процедура еквалізації гістограми зводиться до виконання перетворення за формулою (3.13), що базується лише на інформації, яка може бути витягнута безпосередньо з зображення без вказівки інших додаткових параметрів. Варто також відмітити простоту обчислень, які необхідні для реалізації даного методу.
Зворотне перетворення з s у r визначається наступною формулою:
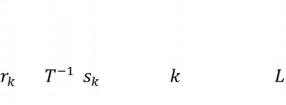
= ( ) |
= 0,1,2,…, −1 |
(3.14) |
Приклад 3.3. Еквалізація гістограми.
На рисунках 3.17(а) представлено ті самі зображення, що і на рисунку 3.15, а на рисунках 3.17(б) - результати виконання перетворень еквалізації гістограми по кожному з цих зображень. Перші три результати демонструють значне покращення. Як і очікувалося, на четвертому зображенні еквалізація гістограми не призводить до появи помітної візуальної різниці, оскільки гістограма цього зображення спочатку займала увесь діапазон значень яскравості. Графіки функцій, по яких робилися перетворення зображень з рис. 3.17(а) у рис.3.17(б), представлені на рис. 3.18. Ці функції були отримані за формулою (3.13) на основі гістограм, показаних на рис. 3.15(б). Відмітимо, що графік перетворення (4) близький до лінійної форми, знову-таки показуючи цим, що рівні яскравості на четвертому зображенні близькі до рівномірного розподілу. Як і очікувалося, ефект від перетворення еквалізації гістограми на такому зображенні незначний.
Гістограми зображень після еквалізації представлені на Рис. 3.17(в). Цікаво відмітити, що хоча усі ці гістограми хоча й розрізняються, проте, еквалізаційні зображення виглядають дуже схожими. Це не є несподіваним, оскільки різниця між зображеннями в лівій колонці полягає тільки в їх контрастах, а не в змісті. Іншими словами, оскільки зображення мають один й той самий зміст, то збільшення контрасту, що отримується шляхом еквалізації гістограми, досить, щоб компенсувати різницю в яскравостях і зробити результуючі зображення візуально невідмітними. На цьому прикладі з зображеннями в лівій колонці, що мають значні різниці в контрастах, ілюструються можливості перетворення еквалізації гістограми як адаптивного інструменту покращення зображень.

Рис. 3.17. (а) Зображення з рисунку 3.15; (б) результати еквалізації гістограми; (в) гістограми зображень після обробки
Рис. 3.18. Функції перетворень (1) -(4) були отримані на основі гістограм зображень на рис. 3.17(а) за допомогою рівняння (3.13).
