
Теорія цифрового зображення (Лекції 1-3)
.pdf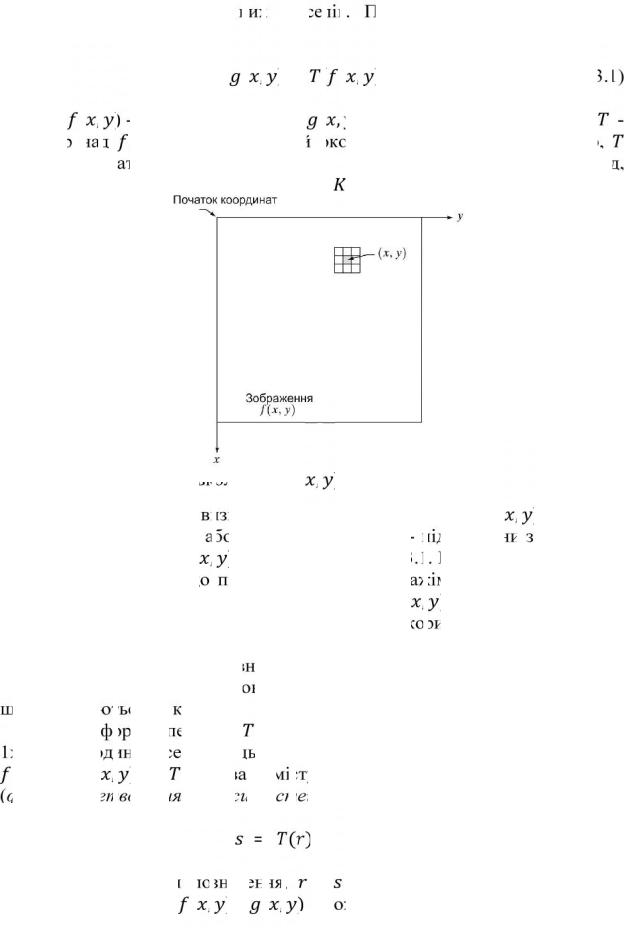
Як було зазначено, термін просторова область відноситься до множини пікселів, що складають зображення. Просторові методи оперують
безпосередньо |
значеннями цих |
пікселів |
|
Процеси |
просторової обробки |
|||
описуються рівнянням |
( , |
) = [ |
( |
, )], |
|
|
||
|
|
|
( |
|||||
Де |
вхідне зображення, |
|
|
- оброблене зображення, а |
||||
оператор (над, |
|
|
околиці точки |
. Більше того, |
||||
, визначений в деякій ( |
,у) |
|
зображень, наприклад, |
|||||
може оперувати над послідовністю |
|
вхідних |
|
(х,у) |
||||
виконуючи поелементне підсумовування |
|
зображень для зменшення шуму. |
||||||
Рис. 3.1. Околиця 3x3 навколо точки |
зображення |
|
|
|||
Головний підхід у визначенні околиці навколо точки |
|
полягає у |
||||
використанні квадратної або прямокутної області |
підмножини( , |
зображення,) |
||||
що центрується в точці |
, як показано на рис. 3 1 Центр цієї підмножини |
|||||
зсувається від пікселя ( , |
пікселя,) |
починаючи, скажімо, з верхнього лівого |
||||
кута. Оператор Т виконується в кожній точці |
, даючи |
в результаті |
||||
вихідне значення g для |
цієї точки. Процес використовує( , ) |
тільки пікселі |
||||
усередині області зображення, обмеженої деякою околицею. Квадратні або прямокутні масиви є, безумовно, найбільш поширеними внаслідок простоти їх реалізації, хоча іноді застосовуються околиці іншої форми, наприклад такі, що наближаються до круга.
|
Проста форма оператора |
досягається у разі, коли околиця має розміри |
||||
1x1 |
(тобто один піксель). В цьому випадку g залежить тільки від значення |
|||||
в |
точці |
, і |
набуває змісту функції градаційного перетворення |
|||
функції перетворення( , ) |
інтенсивностей або функції відображення) виду |
|||||
|
|
|
|
= |
( ) |
( 3.2) |
|
де, для |
простоти |
позначення, |
і |
означають, відповідно, значення |
|
яскравості зображень |
( , ) і |
( , |
в кожній точці (х,у). Наприклад, якщо |
|||
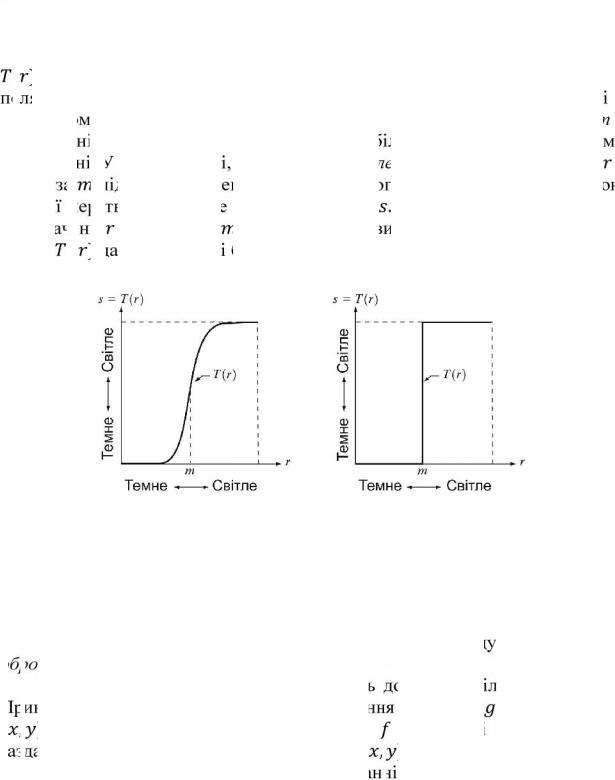
має вигляд, зображений на рис. 3.2(а), то ефект від такого перетворення |
||
полягає( ) |
в отриманні зображення більш високого контрасту в порівнянні з |
|
оригіналом, а також у затемненні пікселів із значеннями меншими за |
і |
|
підвищенні яскравості пікселів із значеннями більшими за m на початковому
зображенні. |
цьому методі, відомому як посилення контрасту, значення - |
менші |
під час наближення до рівня чорного стискаються за допомогою |
функції перетворення у все вужчий діапазон Зворотний ефект має місце
для значень |
більших за . У граничному випадку, зображеному на рис. |
|
3.2(б), |
( ) |
дає в результаті бінарне зображення. |
Рис. 3.2. Градаційне перетворення для покращення контрасту
Відображення такої форми називають пороговою функцією. За допомогою градаційних перетворень можуть бути побудовані деякі досить прості, але дієві методи обробки зображень. Оскільки результат покращення кожного елементу зображення залежить тільки від яскравості цього елементу, методи цієї категорії часто відносять до процедур поелементної
обробки. |
|
|
|
|
Збільшення розмірів околиці призводить |
|
значно більшої гнучкості. |
||
Принцип полягає в тому, що для знаходження значення |
в деякій точці |
|||
використовуються значення функції |
|
усередині |
деякої околиці |
|
(заздалегідь, ), |
заданої форми, що оточує точку |
) |
. Один з основних підходів |
|
у такій постановці базується на використанні( |
так званих масок (також |
|||
згадуваних як фільтри, ядра, шаблони або вікна). Найчастіше маска є невеликим (скажімо, 3x3 елементи) двовимірним масивом, подібним до представленого на рис. 3.1, значення коефіцієнтів маски усередині якого визначають сутність процесу, наприклад, підвищення різкості зображення. Методи покращення засновані на такому підході, часто відносять до обробки за маскою або фільтрації за маскою.
2. Деякі основні градаційні перетворення
Ми розпочинаємо вивчення методів покращення зображень з обговорення функцій градаційного перетворення. Вони належать до найпростіших з усіх методів покращення зображень. Значення пікселів до і
після обробки позначатимуться символами |
і відповідно. Ці величини |
|||||
пов’язані |
виразом |
виду |
|
), де |
перетворенням, що відображає |
|
значення |
пікселя |
в |
значення |
пікселя |
Оскільки ми маємо справу |
|
|
= ( |
|
|
|||
дискретним (квантовим) представленням, значення функції перетворення, як правило, зберігаються в одновимірному масиві, і відображення з у здійснюється за таблицею. У випадку 8-бітового представлення таблиц перетворення, що містить значення , складатиметься з 256 елементів.
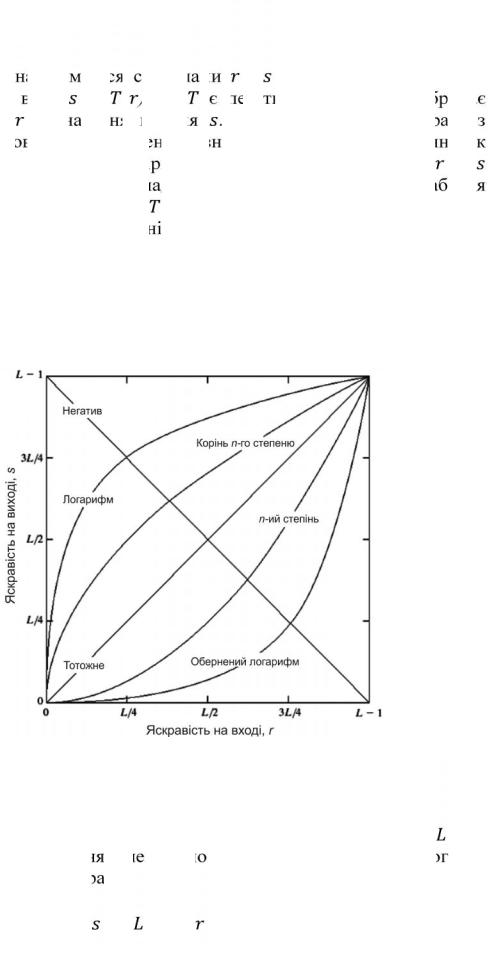
В якості введення в градаційні перетворення розглянемо рис. 3.3, на якому зображені три основні типи перетворень, що часто використовуються для покращення зображень: лінійне (негатив і тотожне перетворення), логарифмічне (логарифм і зворотний логарифм), і степеневе (n-та міра й корінь n-ої міри). Тотожне перетворення є тривіальним випадком, при якому яскравості на виході ідентичні до яскравостей на вході. Воно приведене на графіку тільки для повноти розгляду.
Рис. 3.3. Деякі основні функції градіаційних перетворень, що використовуються для покращення зображень
2.1. Перетворення зображення в негатив |
|
|
Перетворення зображення в негатив з яскравістю в діапазоні |
|
|
здійснюється з використанням негативного перетворення, |
зображеного на |
|
|
[0, −1] |
|
рис. 3.3, що визначається виразом |
|
|
= – 1 – |
|
(3.3) |
Подібне обернення рівнів яскравості зображення створює еквівалент фотографічного негативу. Цей тип обробки особливо підходить для посилення білих або сірих деталей на тлі темних областей зображення,
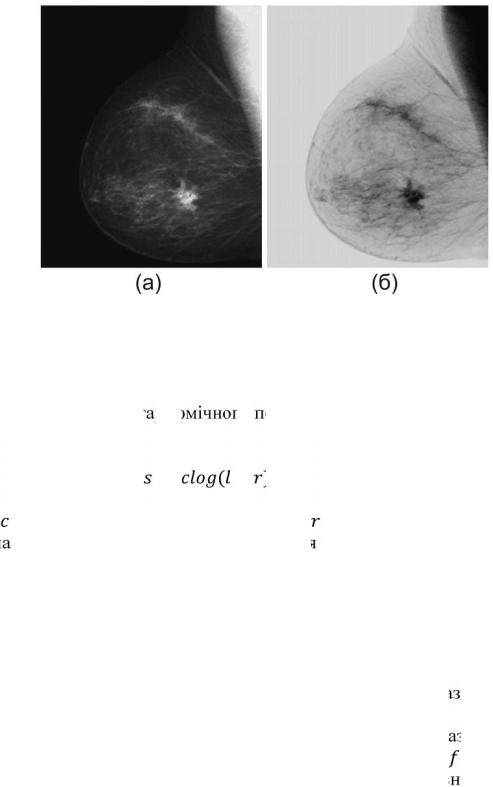
особливо коли темні області мають переважаючі розміри. Приклад зображений на рис. 3.4. На початковому зображенні представлена цифрова рентгенограма молочної залози, що демонструє невелике ураження. Незважаючи на той факт, що візуальний зміст на обох зображеннях є ідентичний, відмітимо, наскільки простіше в даному випадку аналізувати молочну залозу на негативному зображенні.
Рис. 3.4. (а) Початковий вигляд рентгенограми молочної залози; (б) негативне зображення, отримане із застосуванням негативного перетворення за формулою (3.3)
2.2. Логарифмічне перетворення
Загальний вигляд логарифмічного перетворення, показаного на рис. 3.3,
задається формулою |
= |
+ ) |
|
|
|
|
|
|
(3.4) |
||
де |
- константа і передбачається, що |
|
. Форма логарифмічної |
||
кривої |
рис. 3.3 показує, що це перетворення |
перетворює вузький діапазон |
|||
≥ 0 |
|
||||
малих значень яскравостi на початковому зображенні в ширший діапазон вихідних значень. Для великих значень вхідного сигналу вірним є протилежне твердження. Пропонуємо використати цей тип перетворення для розтягування діапазону значень темних пікселів на зображенні з одночасним стисненням діапазону значень яскравих пікселів. Навпаки, під час використанні зворотного логарифмічного перетворення відбувається розтягування діапазону яскравих пікселів і стиснення діапазону темних пікселів.
Будь-яка крива, що має загальний вигляд, близький до показаної на рис. 3.3 логарифмічної функції, здійснюватиме таке розтягування стискнення діапазонів яскравості на зображенні. Насправді для цих цілей значно більше універсальними, ніж логарифмічні, є степеневі перетворення. Незважаючи на

це, логарифмічна функція має важливу особливість, дозволяючи стискати динамічний діапазон зображень, що мають великі варіації в значеннях пікселів. Класичним прикладом, в якому значення пікселів мають великий динамічний діапазон, є спектр Фур’є. В даний момент нас цікавлять лише властивості спектру як зображення. Спектр, значення якого змінюються в діапазоні від 0 до 106 або більше, не є чимось незвичайним. Якщо обробка подібної сукупності значень не представляє проблеми для комп’ютера, то система відтворення зображень зазвичай не здатна правильно відобразити такий великий діапазон значень інтенсивності. Результуючий ефект такий, що під час звичайного відтворення спектру Фур’є значне число деталей втрачається.
В якості ілюстрації логарифмічного перетворення, на рис. 3.5(а) приведено зображення спектру Фур’є, що має значення в діапазоні від 0 до 1,5*106. Якщо масштабувати ці значення лінійно для відображення в 8- бітовій системі відтворення, то найбільш яскраві пікселі домінуватимуть над слабкими значеннями спектру. Ефект такого домінування яскраво ілюструє рис. 3.5(а), на якому тільки дуже мала область зображення не сприймається як чорна.
Рис. 3.5. (а) спектр Фур’є; (б) срезультат= 1 застосування логарифмічного перетворення за формулою (3.4) із
Якщо ж замість подібного способу відтворення ми спочаткус = 1застосуємо до значень спектру перетворення по формулі (3.4) (із в даному випадку), тоді діапазон значень результату буде від 0 до 6,2, що набагато зручніше. На рис. 3.5(б) зображений результат лінійного масштабування нового діапазону і відображення спектру на тому самому 8-бітовому пристрої відтворення. Більшість спектрів Фур’є, які представлені в публікаціях з обробки зображень, масштабуються саме таким чином.
2.3. Степеневі перетворення
Степеневі перетворення мають вигляд
= ( + |
) |
= |
(3.5) |
і |
додатні константи. Деколи рівняння (3.5) записують у вигляді |
||
|
|
для того, щоб ввести зміщення тобто |
вимірювальний |
(ненульовий) вихід, коли на вході нуль. Втім, зміщення виникають під час калібрування пристроїв відтворення, і тому в рівнянні (3.5) вони зазвичай
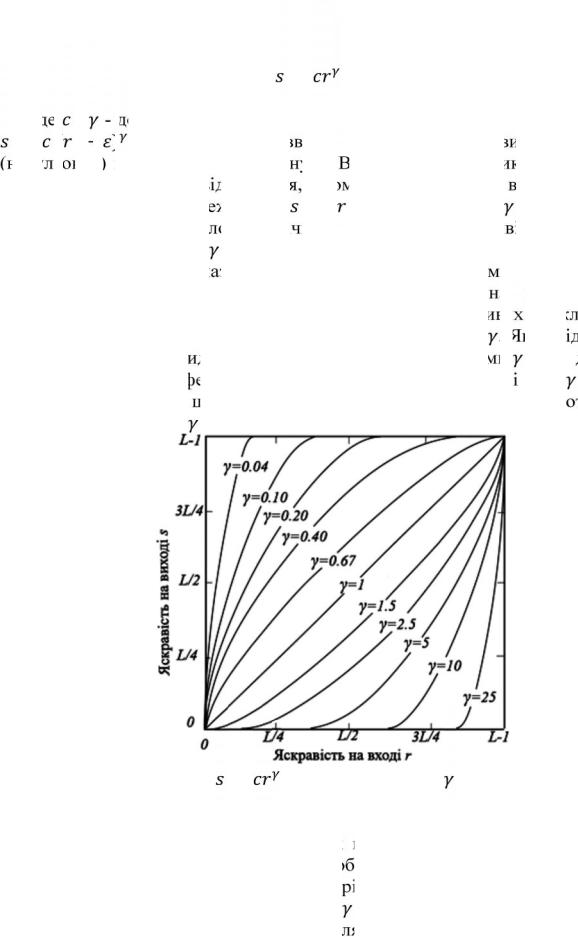
ігноруються. Графіки залежностей від |
за різних значень зображені на |
|
рис. 3.6. Подібно до |
гарифмічного |
перетворення криві степеневих |
залежностей при малих |
відображають вузький діапазон малих вхідних |
|
значень в широкий діапазон вихідних значень, при цьому для великих вхідних значень вірне зворотне твердження. Проте, відміну від логарифмічних функцій, тут виникає ціле сімейство кривих можливого
перетворення, що отримуються простою зміною параметра . |
і слід було |
||
очікувати, на рис. 3.6 видно, що криві, отримані зі значеннями |
при |
|
дають |
прямо протилежний ефект в порівнянні з тими, які отримані |
> 1 |
|
|
Нарешті відмітимо, що рівняння (3.5) перетворюється |
у |
тотожне |
|
|
< 1 |
||
перетворення при с = = 1. |
|
|
|
Рис. 3.6. Графіки рівняння |
для різних значень ( |
у всіх |
випадках) |
|
|
Амплітудна характеристика багатьох пристроїв, що використовуються для введення, друку або візуалізації зображень, відповідає степеневому закону. За традицією, показник степеню в рівнянні степеневого перетворення називають гамма, і саме тому символ використаний в рівнянні (3.5). Процедура, що використовується для корекції такої степеневої характеристики, називається гамма-коррекцією. Наприклад, пристрої з електронно-променевою трубкою (ЕПТ) мають степеневу залежність яскравості від напруги з показником степеню в діапазоні від 1,8 до 2,5. Звертаючи увагу на криву для γ = 2,5 на рис. 3.6, можна бачити, що подібна
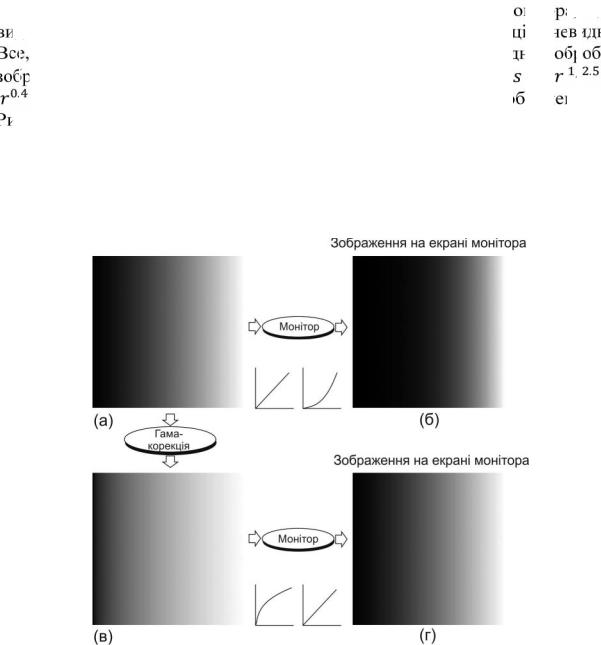
система відображення матиме тенденцію до відтворення зображень темнішими, ніж вони є насправді. Цей ефект ілюструється на рис. 3.7. На рис. 3.7(а) показаний простий півтоновий лінійний клин, що подається на вхід монітора з ЕПТ. Як і очікувалося, зображення на екрані реального монітора виявляється темніше, ніж повинно бути на екрані ідеального монітора, що і видно на рис. 3.7(б). Необхідність застосування гамма-корекції очевидна. Все, що вимагається для компенсації - це зробити попередню= обробку/ =
зображення, що візуалізується, за допомогою перетворення перш, ніж воно потрапить на вхід монітора. Результат зображений на
Рис. 3.7(в). При відтворенні на тому ж моніторі, така гамма-корекція- корекція забезпечує виведення, візуально близьке до оригінального зображення, що й показано на рис. 3.7(г). Аналогічні дослідження мають бути застосовані і по відношенню до інших пристроїв для роботи із зображеннями, таких як сканери і принтери. Єдиною відмінністю між ними має бути значення гамма, залежне від конкретного пристрою.
Рис. 3.7. (а) півтонове зображення з лінійним клином; (б) відгук монітора на лінійний клин; (в) клин після гамма-корекції; (г) результат на екрані монітора.
Гамма-корекція необхідна, якщо потрібно точне відтворення зображення на екрані комп’ютера. Зображення, які не відкориговані правильно, можуть виглядати або як вибілені, або, що ймовірніше, як занадто темні. Правильне відтворення кольорів також вимагає деяких знань з гамма-корекції, оскільки подібне перетворення змінює не лише яскравість, але також співвідношення між червоним, зеленим і синім кольорами. Останніми роками гамма-корекція

стає важливішою, оскільки збільшується комерційне використання цифрових зображень в Інтернеті.
Приклад 3.1. Покращення контрасту за допомогою степеневих перетворень.
На додаток до можливостей гамма-корекції, степеневі перетворення корисні для універсального керування контрастом. На рис. 3.8(а) зображений знімок, отриманий за допомогою ЯМР-томографа (ґрунтованого на ефекті ядерного магнітного резонансу). На ньому зображена грудна частина хребта людини, що має перелом зі зміщенням і поразкою хребетного стовпа. Перелом видно поблизу центру хребта на відстані однієї чверті від верхнього краю знімка. Оскільки зображення переважно темне, бажано здійснити розтягування рівнів яскравості. Це може бути досягнуто за допомогою степеневого перетворення з дробовим (меншим одиниці) показником степеню. Три зображення, що залишилися, отримані шляхом обробки зображення рис. 3.8(а) степеневим перетворенням за формулою (3.5). Значення гамма для зображень(б),(в) і (г) рівні, відповідно, 0,6, 0,4 і 0,3 (значення с рівне 1 в усіх випадках). Можна помітити, що зі зменшенням значення гамма від 0,6 до 0,4 стає видимою все більша кількість деталей. Подальше зменшення гамма до 0,3 дещо посилює деталі фону, але знижує контраст - зображення стає таким що "вилиняло" - це особливо помітно на фонових ділянках. Порівнюючи усі зображення, можна бачити, що найкращий результат в сенсі оцінки контрасту і розпізнавання деталей досягається при = 0,4. Значення = 0,3 можна вважати границею, нижче якої контраст цього конкретного зображення зменшується до небажаного рівня.
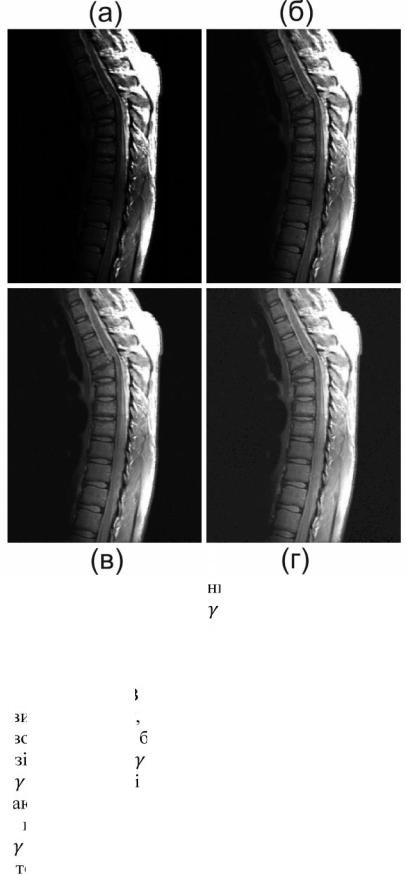
Рис. 3.8. (а) ЯМР-знімок хребта людини з переломом; (б-г) результати |
|
перетворень за формулою (3.5) із с = 1 і |
=0.6. 0.4 і 0,3 відповідно |
Приклад 3.2. Інша ілюстрація степеневого перетворення.
Проблема із зображенням на рис. 3.9(а) протилежна до тієї, яка була із
зображенням на рис. 3.8(а). В даному випадку вимагається покращити зображення, яке виглядає таким, що "вилиняло", що вказує на необхідність пониження яскравості. Це може бути досягнуто за допомогою перетворення
по формулі (3.5) |
значеннями |
більше 1. Результати обробки зображення |
рис. 3.9(а) при |
, 4,0 |
5,0 показані на рис. 3.9(б-г). Найкращі |
= 3,0
результати досягаються при значеннях гамма 3,0 і 4,0, причому останній
варіант виглядає краще, оскільки має більший контраст. На зображенні,
отриманому при = 5,0, є занадто темні області, на яких частина деталей загублена. Такі темні області можна спостерігати в лівому верхньому квадранті, зліва від основної дороги.

Рис. 3.9с. =(а)1аерофотознімок;= 3,0,4,0 і5,0(б) -(г) результати перетворення за формулою (3.5) із і відповідно
2.4. Частково-лінійні функції перетворень
Підходом, що доповнює методи, розглянуті раніше, є використання частково-лінійних функцій. Головна перевага частково-лінійних функцій в порівнянні з вище розглянутими полягає в тому, що їх форма може бути наскільки завгодно складною. Насправді, практична реалізація деяких важливих перетворень може бути здійснена тільки за допомогою частковолінійних функцій. Основний недолік частково-лінійних функцій полягає в тому, що для їх опису необхідно задавати значно більшу кількість параметрів.
2.4.1. Посилення контрасту
Одним з простих випадків використання частково-лінійних функцій є перетворення, що посилює контраст. Низький контраст зображень може бути наслідком поганого освітлення, надмірно великого динамічного діапазону сенсора, або навіть невірно встановленої діафрагми об’єктиву під час зйомки. Посилення контрасту досягається збільшенням динамічного діапазону яскравості на зображенні, що обробляється.
На рис. 3.10(а) показано типове перетворення, що використовується для
посилення контрасту. |
Положення |
точок |
=( |
) і |
задають вигляд |
||
функції перетворення. |
Якщо |
= |
і |
перетворення( , ) |
стає тотожним, |
||
