
- •ВСТУП
- •ТЕМА 1. ЕЛЕМЕНТИ ТЕОРІЇ МНОЖИН
- •1.1. Основні поняття теорії множин. Операції над множинами та їх властивості
- •1.2. Доведення рівностей з множинами
- •Задачі для самостійної роботи
- •1.3. Формули включення-виключення
- •Задачі для самостійної роботи
- •ТЕМА 2. КОМБІНАТОРИКА
- •2.1. Загальні правила комбінаторики
- •Задачі для самостійної роботи
- •2.2. Вибірки та їх класифікація
- •2.3. Сполуки
- •Задачі для самостійної роботи
- •2.4. Розміщення
- •Задачі для самостійної роботи
- •2.5. Перестановки
- •Задачі для самостійної роботи
- •2.6. Сполуки з повтореннями
- •Задачі для самостійної роботи
- •2.7. Розміщення з повтореннями
- •Задачі для самостійної роботи
- •2.8. Перестановки з повтореннями
- •Задачі для самостійної роботи
- •2.9. Формула бінома Ньютона
- •Задачі для самостійної роботи
- •ТЕМА 3. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ ЛОГІКИ
- •3.1. Алгебра висловлювань
- •Задачі для самостійної роботи
- •3.2. Логіка предикатів
- •Задачі для самостійної роботи
- •ВІДПОВІДІ ДО ЗАДАЧ ДЛЯ САМОСТІЙНОЇ РОБОТИ
- •РЕКОМЕНДОВАНА ЛІТЕРАТУРА
5.2. |
A ∆ (B ∆ C) = ( A ∆ B) ∆ C |
(асоціативність) |
5.3. |
A ∩ (B ∆ C) = ( A ∩ B) ∆ ( A ∩C) |
|
(дистрибутивність перетину відносно симетричної різниці)
5.4.A ∆ A =
5.5.A ∆ = A
5.6.A ∆U = A
5.7.A ∆ A =U
Наведені властивості операцій над множинами використовують для спрощення різних виразів і доведення різноманітних рівностей.
Із властивості 4.3 та означення симетричної різниці випливає, що операції різниці та симетричної різниці можуть бути виражені через більш прості операції об`єднання, перетину та доповнення:
A \ B = A ∩ B ,
A ∆ B = ( A \ B) (B \ A) = ( A ∩ B) (B ∩ A) ,
A ∆ B = ( A B) \ ( A ∩ B) = ( A B) ∩( A ∩ B) .
1.2. Доведення рівностей з множинами
Для перевірки та доведення рівностей з множинами можна скористатися будь-яким із трьох методів: графічним методом, методом двостороннього включення чи методом еквівалентних перетворень.
Найпростішим методом перевірки рівностей є графічний метод. Він полягає у порівнянні діаграм Ейлера-Венна для результуючих множин, що задаються відповідно правою і лівою частинами досліджуваної рівності. Якщо ці діаграми повністю співпадають (визначають одну і ту ж саму множину), досліджувана рівність є вірною, інакше – ні.
Задача 1.2.1. Графічним методом перевірити рівність
A \ B = A ∩ B ,
тобто властивість 4.3 операції різниці.
Розв’язання. Діаграма Ейлера-Венна для результуючої множини A \ B із лівої частини досліджуваної рівності має вигляд:
9
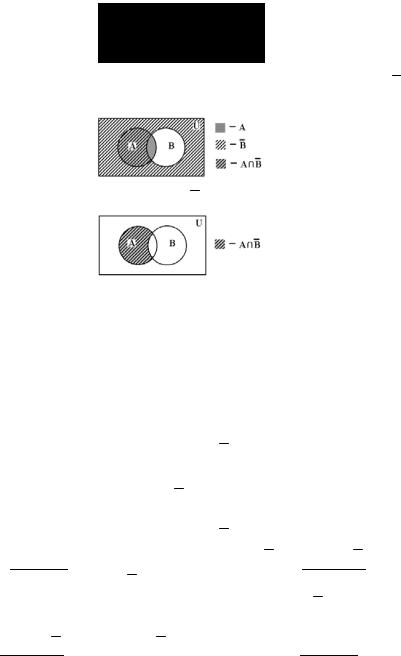
Процес побудови діаграми Ейлера-Венна для множини A ∩ B із правої частини досліджуваної рівності має вигляд:
тобто результуючій множині A ∩ B відповідає діаграма
Очевидно, діаграми для результуючих множин повністю співпадають, отже, досліджувана рівність справді є вірною. ■
Універсальним методом доведення рівностей з множинами є
метод двостороннього включення, який базується на співвідношенні (1.1.1), тобто для доведення рівності вигляду A = B необхідно і досить показати, що A B і B A .
Задача 1.2.2. Методом двостороннього включення довести рівність
A \ B = A ∩ B .
Розв’язання.
1) Покажемо, що A \ B A ∩ B .
Візьмемо довільний елемент x із множини A \ B . Необхідно показати, що тоді обов’язково x A ∩ B . Маємо:
x A \ B x A i x B x A i x B x A ∩ B .
2) Покажемо, що A ∩ B A \ B .
Візьмемо довільний елемент x із множини A ∩ B . Необхідно показати, що тоді обов’язково x A \ B . Маємо:
x A ∩ B x A i x B x A i x B x A \ B . ■
10
Задача 1.2.3. Методом двостороннього включення довести закон де Моргана для операції об’єднання:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
= |
A |
∩ |
B |
. |
|
|
|
|
||
|
Розв’язання. |
||||||||||||||||||||||||
1) |
x |
|
|
|
|
|
|
x A B x A i x B x |
|
i x |
|
|
|||||||||||||
A B |
A |
B |
|||||||||||||||||||||||
|
x |
|
|
|
|
∩ |
|
. |
|
|
|
|
|||||||||||||
|
|
A |
B |
||||||||||||||||||||||
2) |
x |
|
∩ |
|
|
x |
|
i x |
|
x A i x B x A B |
|||||||||||||||
A |
B |
A |
B |
||||||||||||||||||||||
|
x |
|
. ■ |
||||||||||||||||||||||
|
A B |
||||||||||||||||||||||||
Задача 1.2.4. Методом двостороннього включення довести дистрибутивність операції перетину відносно операції об’єднання:
A ∩(B C) = ( A ∩ B) ( A ∩C) .
Розв’язання.
1) x A ∩(B C) x A і x (B C)x A і (x B або x C)
(x A і x B) або (x A і x C)
(x A ∩ B) або (x A ∩C) x ( A ∩ B) ( A ∩C) .
2)x ( A ∩ B) ( A ∩C) (x A ∩ B) або (x A ∩C)
(x A і x B) або (x A і x C)
x A і (x B або x C) x A і x (B C)x A ∩(B C) . ■
Графічним методом та методом двостороннього включення можуть бути перевірені та строго доведені властивості 1.1 – 5.7 операцій над множинами.
Незважаючи на універсальність, недоліком останнього методу є те, що для складних рівностей він стає досить громіздким.
Ефективним методом доведення рівностей з множинами є
метод еквівалентних перетворень. Його суть полягає у використанні властивостей 1.1 – 5.7 операцій над множинами для зведення однієї частини рівності до іншої чи спрощення обох частин до одного і того ж самого проміжного виразу.
Задача 1.2.5. Методом еквівалентних перетворень довести рівності:
1) A ∩(B \ C) = ( A ∩ B) \ C ;
11

2)A \ ( A ∩ B) = A \ B ;
3)A \ (B C) = ( A \ B) \ C ;
4)A ∩ B = A \ ( A \ B) ;
5)( A \ B) ∩( A \ C) = A \ (B C) ;
6)A \ ( A \ (B ∩C)) = A ∩ B ∩C .
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
A ∩(B \ C) |
4=.3 |
A ∩(B ∩ |
|
) |
2=.2 ( A ∩ B) ∩ |
|
|
|
4=.3 ( A ∩ B) \ C . ■ |
|||||||||||||||
C |
C |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
A \ ( A ∩ B) |
4=.3 |
A ∩( |
|
|
) 2=.8 |
A ∩( |
|
|
|
|
) 2=.3 |
|
|
|||||||||||
A ∩ B |
A |
B |
|||||||||||||||||||||||
|
= ( A ∩ |
|
) ( A ∩ |
|
) 2=.7 ( A ∩ |
|
) 1=.1 ( A ∩ |
|
) 1=.5 |
||||||||||||||||
|
A |
B |
B |
B |
|||||||||||||||||||||
=A ∩ B 4=.3 A \ B . ■
3)A \ (B C) 4=.3 A ∩(B C) 1=.8 A ∩(B ∩C) 2=.2 ( A ∩ B) ∩C 4=.3
=( A \ B) ∩C 4=.3 ( A \ B) \ C . ■
4)A \ ( A \ B) 4=.3 A ∩( A \ B) 4=.3 A ∩( A ∩ B) 2=.8 A ∩( A B) 2=.3
=( A ∩ A) ( A ∩ B) 2=.7 ( A ∩ B) 3=.1 ( A ∩ B) 1=.1
=( A ∩ B) 1=.5 A ∩ B . ■
5)( A \ B) ∩( A \ C) 4=.3 ( A ∩ B) ∩( A ∩C) 2=.2 (( A ∩ B) ∩ A) ∩C 2=.1
= ((B ∩ A) ∩ A) ∩C 2=.2 (B ∩( A ∩ A)) ∩C 2=.4 (B ∩ A) ∩C 2=.1
=( A ∩ B) ∩C 2=.2 A ∩(B ∩C) 1=.8 A ∩(B C) 4=.3
=A \ (B C) . ■
6)A \ ( A \ (B ∩C)) 4=.3 A \ ( A ∩(B ∩C)) 4=.3 A ∩( A ∩(B ∩C)) 2=.8
=A ∩( A (B ∩C)) 3=.1 A ∩( A (B ∩C)) 2=.3
12

=( A ∩ A) ( A ∩(B ∩C)) 2=.7 ( A ∩(B ∩C)) 1=.1
=( A ∩(B ∩C)) 1=.5 A ∩(B ∩C) 2=.2 A ∩ B ∩C . ■
Задача 1.2.6. Методом еквівалентних перетворень довести рівносильність обох означень операції симетричної різниці, тобто довести рівність:
( A \ B) (B \ A) = ( A B) \ ( A ∩ B)
Розв’язання.
( A \ B) (B \ A) 4=.3 ( A ∩ B) (B ∩ A) 1=.3 (( A ∩ B) B) ∩ ∩(( A ∩ B) A) 1=.1 (B ( A ∩ B)) ∩( A ( A ∩ B)) 1=.3
=((B A) ∩(B B)) ∩(( A A) ∩( A B)) 1=.7
=((B A) ∩U ) ∩(U ∩( A B)) 2=.6 (B A) ∩( A B) 1=.1
=( A B) ∩( A B) 2=.8 ( A B) ∩( A ∩ B) 4=.3
=( A B) \ ( A ∩ B) . ■
Урівностях, що містять операцію симетричної різниці, слід користуватися властивостями 5.1 – 5.7, якщо це можливо, якщо ж ні – позбутися її згідно будь-якого з означень (вдалий вибір при цьому може значно спростити подальші викладки).
Задача 1.2.7. Методом еквівалентних перетворень довести рівності:
1)A ∆( A ∩ B) = A \ B ;
2)( A ∆ B) ( A ∩ B) = A B ;
3)A∆( A∆B) = B .
Розв’язання.
1)A ∆( A ∩ B) = ( A ( A ∩ B)) \ ( A ∩( A ∩ B)) 1=.9
=A \ ( A ∩( A ∩ B)) 2=.2 A \ (( A ∩ A) ∩ B) 2=.4 A \ ( A ∩B) = A \ B
(дивись задачу 1.2.5). ■
13

2)( A ∆ B) ( A ∩ B) = (( A \ B) (B \ A)) ( A ∩ B) 1=.2 ( A \ B)
(B \ A) ( A ∩ B) 4=.3 ( A∩B) (B ∩ A) ( A ∩ B) 1=.1
=( A ∩ B) ( A∩B) (B ∩ A) 2=.3 (( A ∩(B B)) (B ∩ A) 1=.7
=( A ∩U ) (B ∩ A) 2=.6 A (B ∩ A) 1=.3 ( A B) ∩( A A) 1=.7
=( A B) ∩U 2=.6 A B . ■
3)Перший спосіб (оптимальний).
A ∆( A ∆ B) 5=.2 ( A ∆A) ∆ B 5=.4 ∆ B 5=.1 B ∆ 5=.5 B . ■
Другий спосіб.
A ∆( A ∆ B) = ( A \ ( A ∆ B)) ( ( A ∆B) \ A) .
Оскільки
A \ ( A ∆ B) = A \ ( ( A \ B) (B \ A)) 4=.3 A∩( ( A∩ B) (B ∩ A)) 1=.8
=A∩(( A∩B) ∩(B ∩ A)) 2=.8 A∩(( A B) ∩(B A)) 3=.1
=A∩(( A B) ∩(B A)) 2=.2 A∩( A B) ∩(B A) 2=.1
=A∩(B A) ∩( A B) 1=.1 A∩( A B) ∩( A B) 2=.9
|
|
|
|
|
|
|
2.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2.7 |
|
|
|
|
|
|
|
|
|
|
|
1.1,1.5 |
|
|
|
|||||||||||||||||||||
= A∩( A B) = |
( A∩ A) |
( A∩B) = ( A∩B) = A∩B , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
( A ∆ B) \ A = ( ( A \ B) (B \ A)) \ A 4=.3 (( A∩ |
|
) (B ∩ |
|
|
)) ∩ |
|
2=.1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
B |
A |
A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
∩(( A∩ |
|
|
|
) (B ∩ |
|
|
)) |
2=.3 ( |
|
∩( A∩ |
|
|
)) ( |
|
|
∩(B ∩ |
|
)) |
2=.2 |
|||||||||||||||||||||||||||||||||||
A |
B |
A |
A |
B |
A |
A |
|||||||||||||||||||||||||||||||||||||||||||||||||||
= ( |
|
∩ A ∩ |
|
) ( |
|
|
|
∩ B ∩ |
|
) |
2=.1 ( A ∩ |
|
|
∩ |
|
) ( |
|
∩ |
|
∩ B) |
2=.7 |
||||||||||||||||||||||||||||||||||||
A |
B |
A |
A |
A |
B |
A |
A |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.1, 2.5 |
|
|
|
|
|
|
||||||
= ( ∩ B) ( A ∩ A∩ B) = ( ∩ B) ( A∩ B) |
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1.1,1.5 |
|
|
|
|
|
|
|
|
|
2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= ( A∩ B) |
= A ∩ B = B ∩ A , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
14
