
Zadachni_copy
.pdf
Vк |
m |
V0к . |
(2.30) |
|
|||
|
|
|
|
Внутрішня енергія реального газу залежить не тільки від температури,алей відоб’єму, оскількискладаєтьсязкінетичної енергії теплового руху його молекул та потенціальної енергії притягання. Для молів реальногогазувираз для внутрішньої енергіїмає вид:
|
|
a |
|
|
U C T |
|
|
(2.31) |
|
|
||||
|
V |
V . |
||
Молярна теплоємність газу Ван-дер Ваальса при сталому об’ємі така ж сама, як і для ідеального газу
|
dU |
|
i |
|
|
|||
C |
|
|
|
|
|
R |
, |
(2.32) |
|
2 |
|||||||
V |
|
dT |
|
|
||||
|
|
|
V |
|
|
|
|
|
проте молярна теплоємність при сталому тиску CP залежить відпараметрівстану,іцязалежністьінодібуваєдужескладною.
Рідкий стан речовини є проміжним станом між газоподібнимітвердим.Поверхнярідиниподібна донатягнутої плівки, яка прагне зробити свою поверхню якомога меншою. Це явище називається поверхневим натягом. Сили поверхневогонатягунапрямленіподотичнійдоповерхніідіють нормальнодобудь-якоїлінії,проведеноїнаційповерхні.Фізична величина яка чисельнодорівнюєвідношеннюсилиF, яка діє налініюдовжиноюL,до цієїдовжининазиваєтьсякоефіцієнтом поверхневогонатягу
|
F |
. |
(2.33) |
|
|||
|
L |
|
|
З термодинамічної точки зору коефіцієнт поверхневого натягучисельнодорівнюєроботі,якутреба виконати, щобипри постійній температурі збільшити площу поверхні рідини на одиницю
dA |
|
dS . |
(2.34) |
Робота dAідена збільшеннявільноїенергіїповерхневогошару, тому маєзміст вільноїенергіїодиниціплощіповерхні.
81

Поверхневий натяг призводить до того, що над викривленоюповерхнеюіснуєдодатковий тиск(тискЛапласа), якийдорівнює:
|
|
1 |
|
1 |
|
|
P |
|
|
|
(2.35) |
||
|
R |
R |
. |
|||
|
|
1 |
|
2 |
|
|
Тут R1 іR2 –головнірадіуси кривизни дляданогоелемента поверхні рідини. Додатковий тиск у будь-якій точці поверхні завжди напрямлений уздовж радіуса кривизни в бік центра кривизни.
Висота підняття (опускання) стовпчика рідини у капілярі визначається за формулою
h P |
(2.36) |
g , |
де – густина рідини.
Довільнетвердетілоявляє собоюсистемусконденсованих часток атомів, іонів, молекул, які при будь-яких температурах знаходяться у безперервному коливному русі біля певних положень рівноваги. Найбільш характерною особливістю твердих тіл є збереження своєї форми та об’єму, чого не спостерігається для інших агрегатних станів. Підвищення температури твердого тіла приводить до зміни його розмірів, якуможна кількіснооцінити. При невеликій змінітемператури кожна одиниця довжини твердого тіла змінюється прямопропорційнодозмінитемператури:
l |
const , |
(2.37) |
|
l t |
|||
|
|
де l –прирістlодиницьдовжини припідвищеннітемператури на tградусів, –лінійний коефіцієнттеплового розширення, який вказує на яку величину зміниться одиниця довжини твердого тіла при нагріванні його на 1 К. Для твердих тіл величини досить малі і складають 10–5 – 10–6 град–1.
Якщопочатковудовжинутвердоготіла при 0оС позначити
через l0, то l lt l0 , де lt – його довжина при t |
оC, а |
t t 0 t , то з (2.37) отримаємо: |
|
lt l0 1 t . |
(2.38) |
82

Унаслідок теплового розширення буде збільшуватися й об’ємтвердоготіла. У цьомувипадкулегкоотримати формулу,
анолгічну(2.38): |
1 t , |
|
Vt V0 |
(2.39) |
де величина називається коефіцієнтом об’ємного теплового розширення. Для ізотропноготвердого тіла 3 .
Для одного моля хімічно простого твердого тіла атомна
теплоємність буде дорівнювати: |
|
C 3R . |
(2.40) |
Отримане співвідношення виражає собою закон Дюлонга іПті, якийстверджує,щоатомнатеплоємністьхімічнопростих твердихтілпри достатньовисокихтемпературах єпостійноюі такою, що дорівнює 3R = 25 103 Дж/(моль К).
У випадку коли ізотропне тверде тіло піддане односторонньому розтягу або стиску, співвідношення між величиноюдеформаціїісилами,якієпричиноюцієїдефомації, виражається законом Гука. При пружних деформаціях механічнанапруга пропорційнадеформації
E , |
(2.41) |
де F S – механічна напруга, яка виникає в тілі під дією |
|
сили F, S – площа поперечногоперерізу тіла, – величина, яка характеризує деформацію, Е – модуль Юнга.
Для деформації розтягу l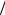 l і називається відносним видовженням. l – абсолютне видовження, l – початкова довжина тіла. Зурахуваннямвищесказаногозакон Гука можна переписатиувигляді:
l і називається відносним видовженням. l – абсолютне видовження, l – початкова довжина тіла. Зурахуваннямвищесказаногозакон Гука можна переписатиувигляді:
F |
E |
l |
|
|
|
|
. |
(2.42) |
|
S |
l |
|||
Методичні поради
1. Загальне правило, яким треба користуватися при розв’язуванні задач, в яких мова йде про реальнігази, полягає у тому, що методи їх розв’язування нічим не відрізняються від методів, які застосовувалися при розв’язуванні задач, у яких фігурувавідеальний газ. Відмінністьлишевтому, щорівняння стануідеальногогазузамінюється скрізьна рівнянняВан-дер- Ваальса (2.26).
83

2.Деякуспецифікумаютьзадачівякихпотрібнорозглянути ефектДжоуля–Томсона,якийвластивийтількиреальнимгазам. Тут слідрозрізняти два випадки:а) розширення газув пустоту, при якому зовнішня робота не виконується, оскільки Р = 0, а також dQ = 0, бо немає зовнішнього середовища, з яким можливий теплообмін. Отжеумова розширеннягазувпустоту:
dU 0 або U const;
б)диференціальний ефектДжоуля–Томсона, колигазперетікає черезпориступерегородкупрималомуперепадітисків.У цьому випадку внутрішня енергія газу змінюється. Але залишається сталою теплова функція стану (ентальпія)
U PV const .
3. При розв’язуванні задач на капілярні явища слід пам’ятати, що додатковий тиск P завжди обчислюється за загальною формулою (2.35), яка в залежності від умови задачі набуваєтогочиіншогоконкретноговигляду.Укапілярнійтрубці радіусом r, меніск є сферичним сегментом радіусом
r R cos ,
де – крайовий кут, тобто кут між стінкою капіляра і дотичною до меніска, проведеною у точці дотику меніска зі стінкою капіляра. Оскільки радіуси кривизни нормальних перерізів сфери однакові, тобто R1=R2=R, то
P 2 2 cos .
R r
Якщо поверхня рідини є частиною циліндричноїповерхні (наприклад, коли рідина міститься між двома довгими плоскопаралельними пластинками), то радіус кривизни нормальногоперерізуповерхнірідини, щопаралельнийтвірній циліндра R1= , R2=R, тоді
P |
|
|
cos |
|
2 cos |
|
|
R |
r |
d , |
|||||
|
|
|
|||||
де d = 2r – відстань між пластинами.
Випадок, коли 0 називається повним змочуванням, а коли – повним незмочуванням.
84

Прикладирозв’язуваннязадач
1. Користуючись рівнянням Ван-дер-Ваальса, обчислити тиск1,1кгвуглекислогогазу,щознаходитьсявбалонімісткістю 20 л при температурі 13 ОС. Результат порівняти з тиском ідеального газу за тих самих умов.
Розв’язання
Рівняння Ван-дер-Ваальса має вигляд
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
|
|
V b RT |
. |
||||
|
|
|||||||
|
V 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Звідки |
|
|
|
RT |
|
a |
|
|
|
P |
|
|
, |
|
|||
|
|
|
|
|
||||
|
|
V b |
V 2 |
|
|
|||
де a 3,64 105 Н кмоль2 ; b 0,043 м3
кмоль2 ; b 0,043 м3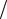 кмоль .
кмоль .
Кількість кіломоліввуглекислогогазудорівнює
m 1,1 0,025кмоля .44
Об’єм, щозаймає один кіломоль вуглекислогогазу, дорівнює
0,02 0,8 м3 кмоль;
0,025
P 8,32 103 Дж/ кмоль град 286град
0,8 м3 /кмоль 0,043 м3 /кмоль
|
3,64 105 Н 4 /кмоль2 |
25,4 105 Н / м2 . |
|
0,82 м6 /кмоль2 |
|||
|
|
Тиск, що обчислюється за рівнянням Клапейрона – Менделєєва
P RT
V
8,31 103 Дж/ кмоль К 286 К 29,7 105 Н / м2. 0,8 м3 /кмоль
85

Останнійрезультатвідрізняєтьсявідрезультату,одержаного при урахуванні поправок а та b, на величину Р=4,3 105 Н/м2, щодаєвідноснупохибку
|
P |
4,3 105 |
|
|
|
|
|
|
0,169. |
|
|
|
||
|
P 25,4 105 |
|
||
Відповідь: P 25,4 105 |
Н / м2 ; P P 0,169 . |
|||
2. Вивести формулу диференціального ефекту Джоуля – Томсона для одного моля газу Ван-дер-Ваальса. Вважати зміну температури малоюізнехтувати вищими степенями сталихаіb.
Розв’язання
При диференціальномуефектіДжоуля –Томсона, коли газ переходить з одного об’єму V1 в інший V2 внаслідок малого перепаду тисків, параметри стану газу змінюються від P1,
V1, T1 до P1 = P1–dP, V2, T2 = T1–dT, причому P>>dP, T>>dT.
У такому процесі
U1 P1V1 U2 P2V2 .
Якщо скористатися співвідношенням (2.31), виразити PV з рівняння Ван-дер Ваальса та урахувати відповідні наближення, цеспіввідношення можна звести до вигляду
|
|
C T |
|
a |
RT Pb |
|
a |
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
V |
1 |
|
V |
1 |
1 |
V |
|
|
|
|
||||||||
|
|
|
|
|
|
a |
1 |
|
|
|
1 |
|
|
a |
. |
(1) |
||||
C |
T dT |
|
R T dT P dP b |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||
V |
1 |
|
|
|
V2 |
1 |
|
1 |
|
V2 |
|
|||||||||
З(1)випливає, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
CV R dT |
|
|
|
|
1 |
|
1 |
|
|
|
|||||||||
|
bdP |
|
|
|
|
|||||||||||||||
|
|
V |
(2) |
|||||||||||||||||
|
2a V |
. |
||||||||||||||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
2 |
|
|
||||||
Величину |
|
|
|
можна наближено обчислити, якщо |
||||||||||||||||
|
|
|
||||||||||||||||||
|
V1 |
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
вважати газ ідеальним, а температуру практично сталою. Тоді
|
|
|
|
|
|
|
1 |
|
1 |
|
|
dP |
|
PV RT |
, P V |
RT |
T |
|
|
|
|
|
.Отже |
||||
|
|
|
|
||||||||||
T ,звідки |
|
|
|
|
|
RT |
|||||||
1 1 |
1 |
2 2 |
|
2 1 |
2 |
V1 |
|
V2 |
|
|
|||
86
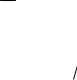
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
у (2), матимемо |
|
||||||
|
|
|
|
|
|
||||||||
підставивши вираз для V V |
2 |
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
2a |
|
|
|
||||||
dT |
|
|
|
|
|
|
|
|
|
dP |
. |
(3) |
|
|
|
|
|
|
|
|
|
||||||
CV |
R |
CV R RT |
|||||||||||
З формули (3) видно, що в досліді Джоуля – Томсона реальнийгазприa=0нагрівається,априb=0–охолоджується.
3. Яку роботу проти сил поверхневого натягу необхідно виконати, щоб надути мильну бульбашку радіусом 5 см? Чому дорівнює додатковий тиск Лапласа всередині бульбашки? = 0,04 Н/м.
Розв’язання
Мильна бульбашка являє собою дуже тонку плівку мильного розчинуприблизносферичноїформи.Цяплівка маєдвіповерхні– внутрішнюізовнішню.Нехтуючитовщиноюплівкиівважаючитому радіусиобохповерхоньоднаковими,знайдемоїхзагальнуплощу:
S 4 R2 4 R2 8 R2 .
Оскільки до утворення бульбашки поверхня, з якої вона була видута – мала, то можна вважати, що S виражає приріст площі поверхні мильного розчину S. Користуючись формулою (2.34), одержуємо:
A S 0,04 Н 8 3,14 0,0025м2 2,5мДж .
м
Додатковий тиск Лапласа для мильної бульбашки можна обчислити за формулою (8.9)
P |
4 |
|
4 0,04Н м |
3,2Па . |
R |
|
|||
|
|
0,05м |
||
Відповідь: P 3,2Па.
4. У бензол ( = 0,03 Н/м) занурено капіляр, внутрішній діаметрякогостановить0,4мм.Знайтивагубензолу,щоувійшов укапіляр за умови повногозмочування.
87

Розв’язання
Вага бензолу, щоувійшов укапіляр:
P mg gV g r2h,
де m – маса бензолу; r – внутрішній радіус капіляра. Висота підняття бензолув капілярі
2 h gr .
Підставивши вираз для h у вираз для Р, отримаємо
P 2 r ;
P 2 3,14 2 10 4 м 0,03Н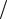 м 3,8 10 5 Н .
м 3,8 10 5 Н .
Відповідь: P 3,8 10 5Н .
Задачі для самостійного розв’язування
2.89.Яку температуру мають 2 г азоту, що займає об’єм 820 см3 при тиску 2 атм? Газ розглядати як: а) ідеальний, б)реальний.
2.90.10 г гелію займають об’єм 100 см3 при тиску 108 Па. Знайти температуру газу, розглядаючи його як: а) ідеальний, б)реальний.
2.91.У закритій посудині об’ємом V = 0,5 м3 знаходиться 0,6 моль вуглекислого газу під тиском 3 106 Па. Користуючись рівнянням Ван-дер-Ваальса, знайти, у скільки разів потрібно збільшити температуру газу, щоб тиск збільшився вдвоє.
2.92.У посудині місткістю 10 л знаходиться 0,25 кг азоту при температурі27 ОС. а) Якучастинутискугазускладаєтиск, зумовлений силами взаємодії між молекулами? б) Яку частину об’єму посудини складає власний об’єм молекул?
2.93.Було запропоновано багато емпіричних та напівемпіричних рівнянь, що описують стани реальних газів. Нижче наведено деякі з них.
|
a |
|
|
РівнянняБертло: P |
V b RT . |
||
|
|||
|
TV 2 |
|
|
|
|
88

|
|
a |
|
|
|
|
|
||
РівнянняКлаузіуса: |
P |
|
V b . |
|
|
|
|||
|
2 |
|
|
|
|||||
|
|
T V |
|
|
|
|
|
||
|
|
c |
|
|
|
|
|
||
|
|
|
|
|
|
|
a |
||
ПершерівнянняДітерічі: P V |
b RT exp |
|
|
. |
|||||
|
|
||||||||
|
|
|
|
|
|
|
RTV |
||
|
|
|
|
a |
|
|
|
|
|
Друге рівняння Дітерічі: |
P |
|
|
|
V b RT |
, де a, b, c |
|||
|
|
|
|||||||
|
V5 3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
–постійнівеличини.Знайтидляцихрівнянькритичніпараметри
Pкр, Vкр, Tкр, значення критичного коефіцієнта RTкр/(PкрVкр) та температури Бойля.
2.94.Яку частинускляноїампули повинен займати рідкий ефірпри20 ОС,щобприйогонагріванніможнабулоспостерігати перехід речовини у критичний стан? Молярна маса ефіру 74 г/моль, густина 714 кг/м3 при 20 ОС, критична температура 194 ОС, критичнийтиск35,6атм.
2.95.Визначити тиск повітря (у мм рт.ст.) у повітряній бульбашці діаметром d = 0,01 мм, яка знаходиться на глибині h = 20 смпідповерхнеюводи.ЗовнішнійтискP1 = 765ммрт.ст.
2.96.У посудину зі ртуттю занурено відкритий капіляр внутрішнімдіаметромd = 3мм. Різницярівнівртутівпосудині
ікапілярідорівнює h = 3,7мм.Чомудорівнюєрадіускривизни ртутногоменіска в капілярі?
2.97.У посудину з водою занурено відкритий капіляр внутрішнімдіаметром d = 1 мм. Різницярівнів води впосудині
ікапілярі дорівнює h = 2,8 см. 1) Чому дорівнює радіус кривизнименіскавкапілярі?2)Якоюбулабрізницярівніврідини в посудиніта капілярі, якщоб змочування булоповним?
2.98.На яку висоту підніметься бензол у капілярі з внутрішнім діаметром 1 мм? Змочування вважати повним.
2.99.Яким повинен бути діаметр пор угнотікерогаза, щоб гасзмігпіднятисянависоту10см?Поривважатициліндричними трубками, які повністю змочуються гасом.
2.100. Капіляр, внутрішнім радіусом 2 мм, занурено в рідину. Вага рідини, щопідняласяукапілярі, дорівнює9 10–4 Н. Знайтизацимиданнимикоефіцієнтповерхневогонатягурідини.
89
2.101. Між двома вертикальними плоско–паралельними склянимипластинками,щознаходятьсянавідстані0,25ммодна відодної,налиторідину.Знайтигустинурідини,якщокоефіцієнт поверхневого натягу становить 0,03 Н/м і висота, на яку вона підняласяміжпластинками,дорівнює3,1см.Змочуванняповне.
2.102. Скляна капілярна трубка внутрішнім діаметром d = 0,2 мм та довжиною l = 20 см вертикально опускається у воду. Верхній кінець трубки запаяний. Який відрізок x трубки повинензнаходитисяпідводою, щобрівніводи укапілярііпоза нимбули однаковими? ТискповітряP0 = 105 Па, = 0,073Н/м.
2.103. Обчислити приріст вільної енергії F поверхневого шарувпроцесізлиттядвоходнаковихкрапельртутіводну.Процес вважати ізотермічним, радіус крапель до злиття r = 2,5 мм.
2.104. Дві мильнібульбашки радіусами R1 = 2 см і R2 = 3 см зливаютьсяводну.Визначитиенергію,щовиділяєтьсяприцьому процесі,якщокоефіцієнтповерхневогонатягу = 0,045Н/м.
2.105.Якакількістьенергіїпоглинаєтьсяприрозбиттівеликої краплини води масою2 г на дрібнікраплини радіусом10–5 см?
2.106. Користуючись законом Дюлонга і Пті, знайти, з якого матеріалувиготовленометалевукулькумасою0,025кг,якщовідомо, щодляїїнагріваннявід10ОС до30ОС затрачено117Дж тепла.
2.107. Свинцева куля, яка летить зі швидкістю 400 м/с, вдаряється об стінку і застрягає в ній. Вважаючи, що 10 % кінетичноїенергіїкулівитрачаєтьсяна їїнагрівання, знайти, на скільки градусів вона нагрілася. Питому теплоємність свинцю знайти за законом Дюлонга і Пті.
2.108.Якісилитребаприкластидокінцівсталевогостержня з площею поперечного перерізу S = 10 см2, щоб не дати йому розширитися при нагріваннівід t1 = 0 ОС до t2 = 30 ОС?
2.109.Притемпературі0 ОСдовжинаалюмінієвогостержня l =50 см, а залізного на l = 0,5 мм більше. Перерізи стержнів однакові. При якій температурі t1 будуть однакові довжини стержнів і при якій температурі t2 будуть однакові їх об’єми?
2.110.Довжина металевогостержняпри температурі20 ОС становить500,12 мм;післянагрівання йогодо100 ОС довжина стержнястала такою,щодорівнює500,6мм. Визначити зякого матеріалу зроблено стержень.
90
