123 / 29-35

29. Линии влияния поперечных сил в трехшарнирной арке.

Способ наложения: пусть сечение К имеет координаты , и угол наклона . Л.в. поперечной силы в этом сечении строится на основании ее общего выражения

Значит, л.в. можно получить, построив л.в. Н и и затем умножив их на соответствующие коэффициенты и сложив ординаты.

Порядок построения л.в. методом нулевых точек:

1. найти 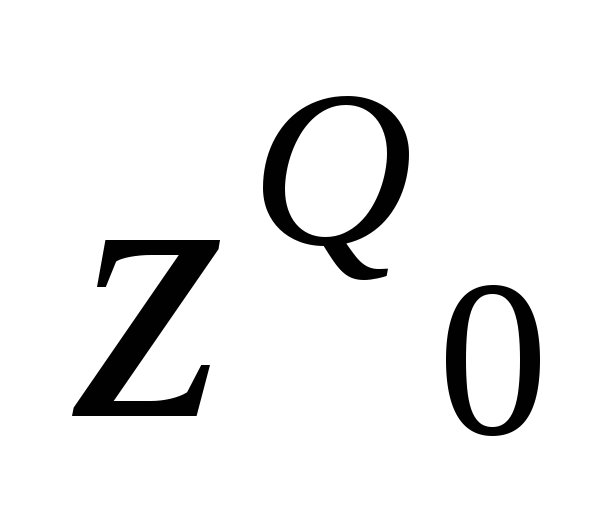и отметить нулевую точку на линии влияния,

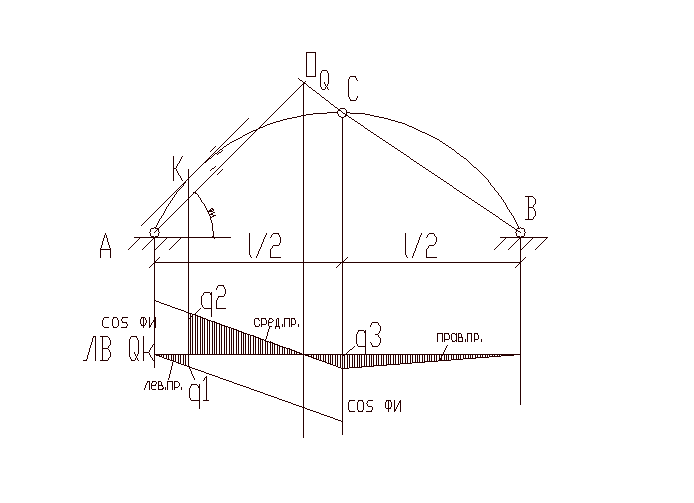
2. под шарниром А отложить ординату , через полученную точку и нулевую точку провести среднюю прямую (справедливую между сечением К и шарниром С),

3. параллельно средней прямой через шарнир А провести левую прямую ( справедливую между опорой А и сечением К),

4. ординату средней прямой под шарниром С соединить с нулем под опорой В – правая прямая.

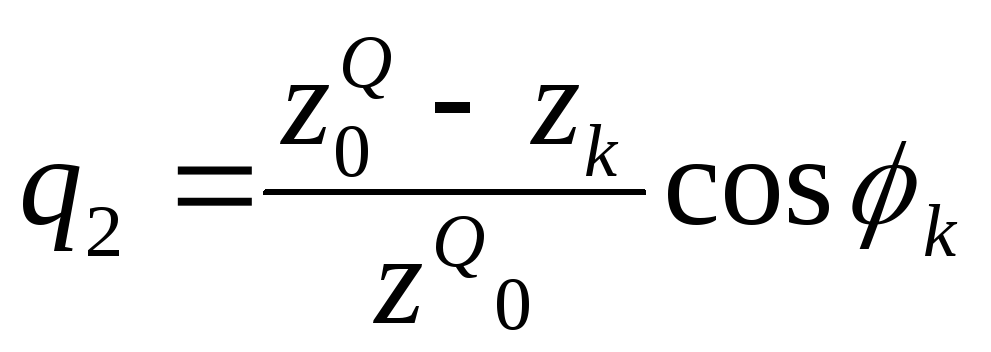
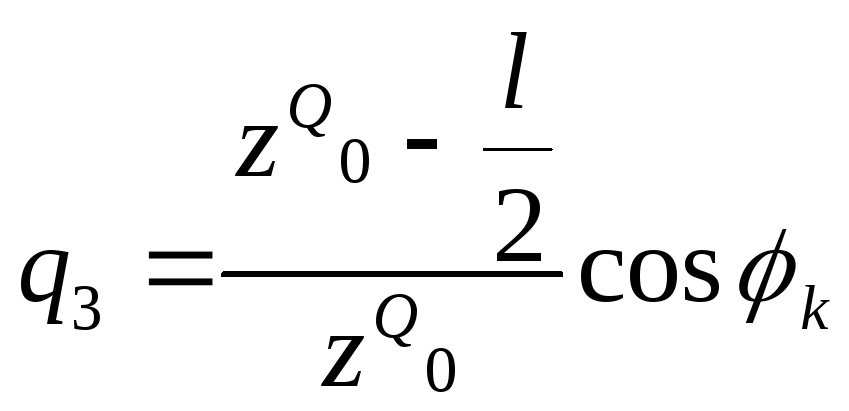
30. Линии влияния продольных сил в трехшарнирной арке.

Способ наложения: пусть сечение К имеет координаты , и угол наклона . Л.в. продольной силы в этом сечении строится на основании ее общего выражения

Значит, л.в. можно получить, построив л.в. Н и и затем умножив их на соответствующие коэффициенты и сложив ординаты.

Порядок построения л.в. методом нулевых точек:

1. найти 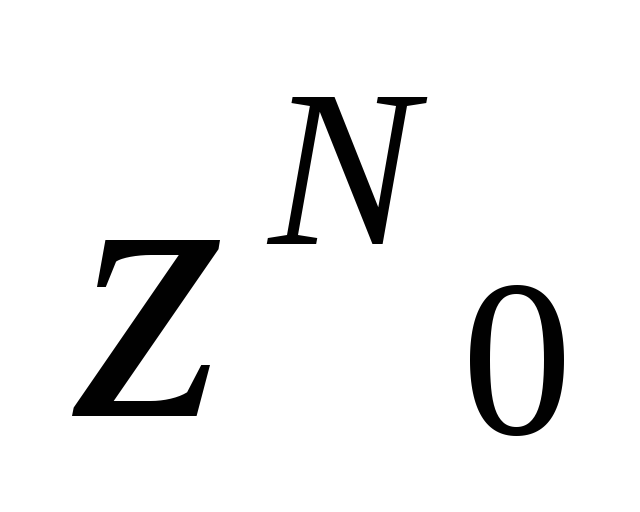и отметить нулевую точку на л.в.,

2. под шарниром А отложить ординату (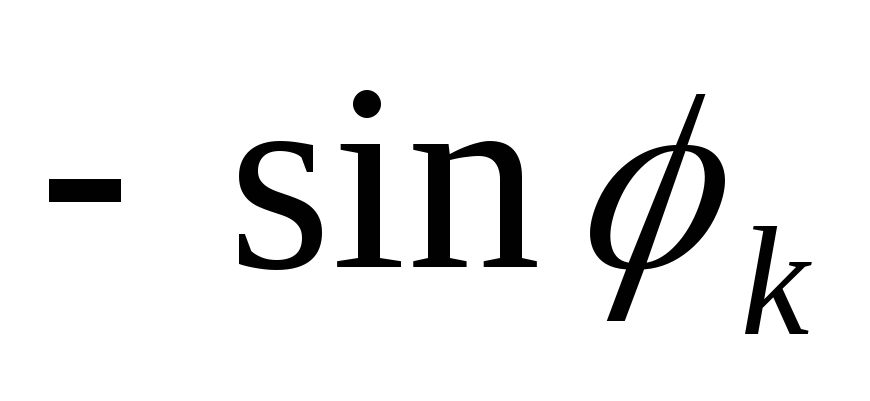), через полученную точку и нулевую точку провести среднюю прямую (справедливую между сечением К и шарниром С),

3. параллельно средней прямой через шарнир А провести левую прямую ( справедливую между опорой А и сечением К),

4. ординату средней прямой под шарниром С соединить с нулем под опорой В – правая прямая.

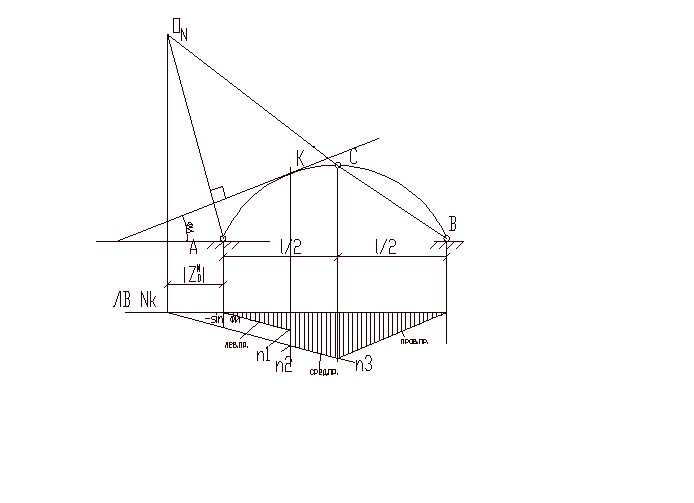
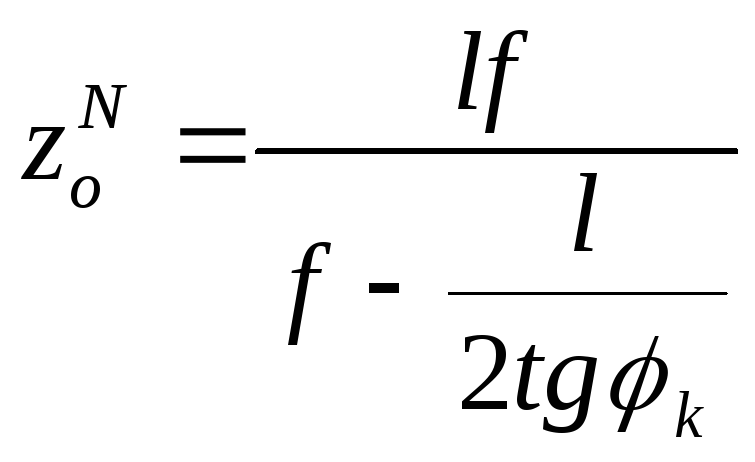
31. Рациональное очертание оси трехшарнирной арки. Определение напряжений в арке. Расчетное положение нагрузки на арке.

Рациональной осью арки называется ось такого очертания, при которой размеры поперечного сечения будут наименьшими. Т.к. наибольшее влияние на прочность оказывают изгибающие моменты, то рациональной осью будет такая, при которой изгибающие моменты во всех сечениях арки будут равны 0.

Уравнение рациональной оси:

;

При вертикальной нагрузке рациональная ось подобна эпюре изгибающих моментов.

Если М=0, то на основании дифференциального соотношения Q=dM/dS Q=0. В сечениях арки возникают только продольные силы N, т.е. арка работает на сжатие. Это особенно выгодно для каменных и бетонных сооружений.

Арка представляет собой кривой стержень, поэтому при точном ее расчете надо учитывать кривизну. Но применяемые в строительстве арки и своды в большинстве случаев пологие. Их допускается рассчитывать по приближенным формулам, т.е. считать что напряженное состояние в арке является таким, как в прямом, а не кривом стержне.

Нормальные напряжения в рассматриваемом сечении арки при наличии продольной силы N и изгибающего момента М ( внецентренном сжатии) определяются:

F – площадь поперечного сечения, J – момент инерции сечения относительно главной оси инерции, перпендикулярной оси изгиба.

Прочность материала арок проверяется по нормальным напряжениям в крайних точках поперечных сечений. Нормальные напряжения зависят от изгибающих моментов М и продольных сил N. Можно раздельно рассматривать линии влияния и и исследовать несколько положений нагрузки на арке. Порядок расчета следующий:

32. Общая формула для определения перемещений.

Пусть плоская система из прямолинейных стержней деформировалась и ее точки получили малые перемещения. Вырежем малый элемент dS, который испытывает деформации удлинения, сдвига и изгиба. Левое сечение его будем считать неподвижным. Обозначим ΔS, Δy, Θ – удлинение, сдвиг, угол поворота сечения. Требуется определить перемещение Δ точки К. Для этого сформируем вспомогательное единичное состояние той же системы: по направлению искомого перемещения приложим единичную силу и определим возникшие от нее внутренние усилия M, Q, и N. Приращениями dM, dQ, и dN будем пренебрегать. Единичное состояние является состоянием равновесия, тогда согласно принципу возможных перемещений сумма возможных работ сил этого состояния на любых возможных перемещениях равна 0.

Внешняя сила cовершает на перемещении Δ возможную работу . Внутренние усилия , , на перемещениях ΔS, Δy, Θ - .

Полную работу внутренних сил получим интегрированием:

, ,

- общая формула для перемещений в плоской системе.

Для пространственной стержневой системы аналогично

Замечание:

1. по этим формулам можем найти не только линейное, но и угловое перемещение, приложив в единичном состоянии к системе единичный момент.

2. При использовании формул несущественно, от чего возникают деформации системы: от нагрузки, изменения температуры, смещения опор и т.д. Важно лишь то, что они д.б. известны. Стержневая система может быть как статически определима, так и неопределима.

3. При определении работ внутренних сил каждому перемещению соответствует своя сила, которая не вызывает перемещений в других направлениях. Это справедливо для прямых стержней и стержней малой кривизны. Для стержней большой кривизны N кроме удлинения вызывает поворот сечений, а М кроме поворота – удлинение эл-та. Поэтому эти силовые факторы совершают допустимую работу на допустимых перемещениях.

33. Формула Мора для плоской стержневой системы.

Из общей формулы для определения перемещений Δ получим зависимость, позволяющую найти перемещения от различных внешних нагрузок.

Внутренние усилия в грузовом состоянии обозначим , , . Выразим через них перемещения в сечении эл-та dS – ΔS, Δy, Θ. Используя ф-лы сопромата

, .

Обозначим через γ угол сдвига

Поперечная сила Q в сечении является статическим эквивалентом касательных напряжений τ. Если бы они распространялись равномерно по сечению как при чистом сдвиге, то вычислялись бы . Но при изгибе значение τ меняется по высоте сечения. Примем, что , η – коэффициент, учитывающий неравномерность распределения τ по сечению, безразмерный, зависит только от формы сеч.

По з-ну Гука при сдвиге , где G – модуль сдвига.

, .

При изгибе сечение поворачивается, а оси искривляется. Используя

, получим .

Подставив в общую формулу, получим

- ф. Мора,

где , , - внутренние усилия в грузовом состоянии, , , - внутренние усилия единичного состояния от единичного усилия, приложенного в направлении искомого перемещения Δ, EA, GA, EJ – жесткости при работе на растяжение/сжатие, сдвиг и изгиб.

34. Формула Мора для пространственной стержневой системы.

Будет содержать 6 слагаемых. Для ее вывода необходимо выразить перемещения ΔS, Δy, Δx, φ, , , , , , , , . Получим

35. Техника вычисления интегралов Мора.

Основной недостаток определения перемещений по формуле Мора – необходимость составления интегрального выражения подынтегральной функции. Часто интеграл Мора удобно использовать не через первообразные функций, а численный метод с использованием эпюр внутренних усилий. Этот способ называют способом перемножения эпюр.

1. Способ Верещагина А.К.

Р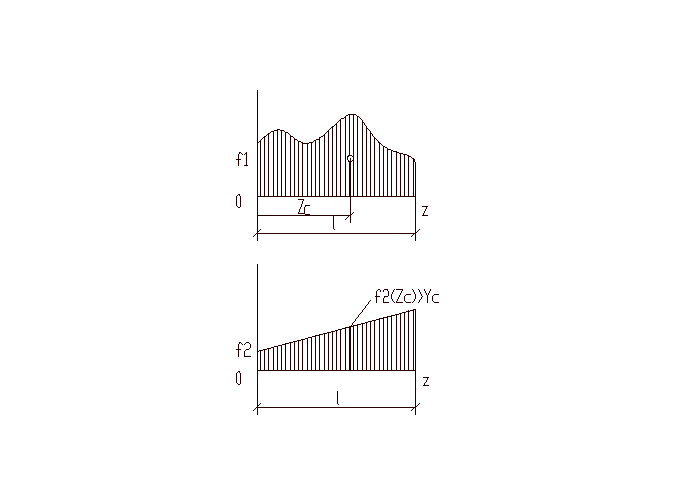ассмотрим 2 прямолинейных участка длины l, допустим требуется вычислить интеграл при условии, что хотя бы 1 из функций линейна. Пусть линейна вторая ф-ция , b, k=const. Исходный интеграл равен .

- площадь эпюры, ограниченной . Второй интеграл представляет собой статический момент фигур с площ. Ω относительно у. Его можно выразить через координаты ЦТ , - координата ЦТ площади фигуры. , выражение в скобках представляет собой значение функции f2 в точке с координатой Zc. . Тогда

- формула Верещагина.

Ордината Yc всегда берется из прямолинейной эпюры, если обе эпюры криволинейны, то данный способ не применяется.

2. Способ Симпсона.

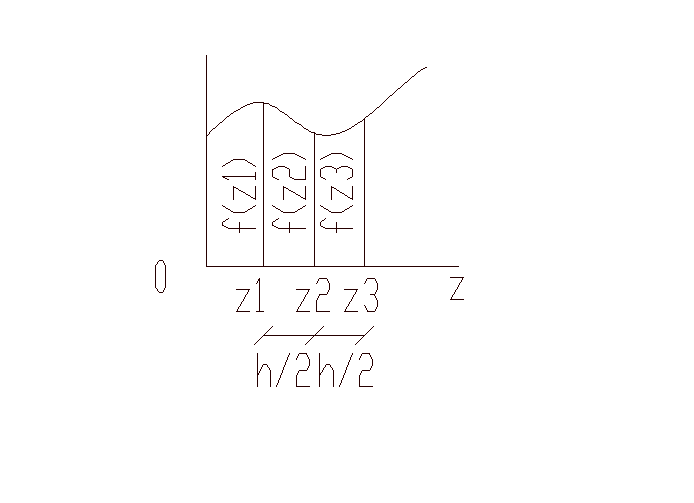
Определенный интеграл от функции f(z) на отрезке [z1, z3] вычисляется след образом:

Пусть ф-ция f(z) представлена в виде f(z)=f1(z)f2(z). Для удобства изобразим эти ф-ции в виде эпюр.

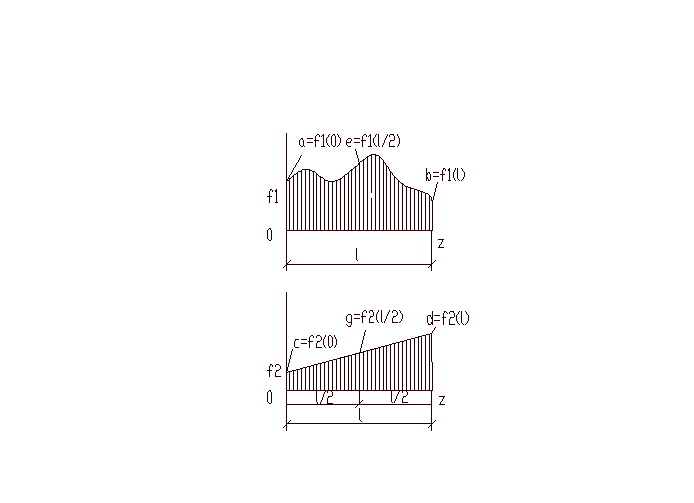
Искомый интеграл по Симпсону будет равен

- формула Симпсона.

В частном случае, когда линейны обе эпюры, то
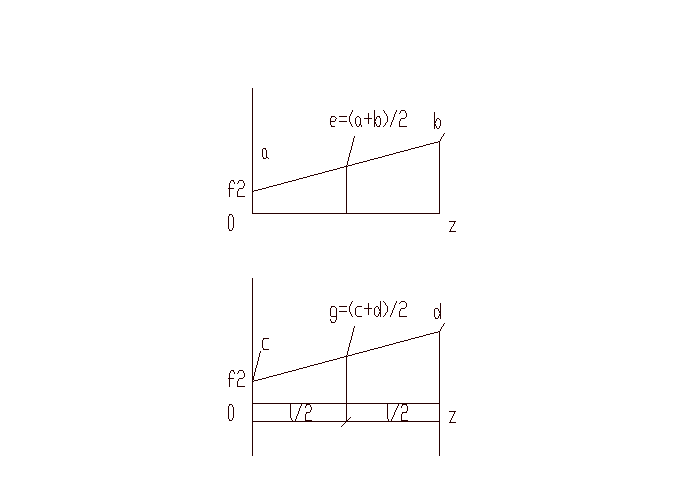