
Lab_2_Старые / №2
.pdf
ЛАБОРАТОРНАЯ РАБОТА №2.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пусть функция y = f (x) определена на отрезке [a; b], a < b. Выполним следующие действия.
1. С помощью точек xo = a, x1, x2, …, xn = b (xo < x1 < x2 < … xn) разобьем отрезок [a; b] на n частичных отрезков
[xo, x1],[x1, x2], …, [xn-1, xn].
2. В каждом частичном отрезке выберем произвольную точку
ci [xi-1,xi]
ивычислим значение функции в ней, т.е. величину f (ci).
3.Умножим найденное значение функции f (ci) на длину
∆xi = xi – xi-1
соответствующего частичного отрезка:
f(ci) ∆xi .
4.Составим сумму Sn всех таких произведений:
Sn = f (c1 )∆x1 + f (c2 )∆x2 +... + f (cn )∆xn = ∑n f (ci )∆xi
i=1
Такая сумма называется интегральной сумой функции y = f (x) на отрезке [a; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max∆xi
(i = 1,2,…,n).
5. найдем предел интегральной суммы, когда n → ∞ так, что λ → 0.
Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции y = f (x) на отрезке
b
[a; b] и обозначается ∫ f (x)dx . Таким образом,
a
b |
|
∑n |
|
∫ f (x)dx = nlim→∞ |
f (ci )∆xi |
||
a |
(λ→0) |
i=1 |
|
Числа а и b называются соответственно нижним и верхним пределами интегри-
рования, f (x) – подынтегральной функцией, f (x)dx – подынтегральным выражением, x – переменной интегрирования, отрезок [a,b] – областью (отрезком) ин-
тегрирования.
Функция y = f (x), для которой на отрезке [a,b] существует определенный инте-
b
грал ∫ f (x)dx , называется интегрируемой на этом отрезке.
a
Теорема. Если функция y = f (x) непрерывна на отрезке [a,b], то определенный
b
интеграл ∫ f (x)dx существует.
a
Отметим, что непрерывность функции является достаточным условием ее интегрируемости, однако определенный интеграл может существовать и для некоторых
1

разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
b
Пусть требуется найти определенный интеграл ∫ f (x)dx от непрерывной функции
a
f (x). Если можно найти первообразную F (x) функции f (x), то интеграл вычисляется по формуле Ньютона-Лейбница:
b
∫ f (x)dx = F(b) −F(a) .
a
Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается че-
рез элементарные функции. В этих и других случаях (например, если функция задана графически или таблично) прибегают к приближенным формулам. С помощью которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла – формулу прямоугольников, формулу трапеций, форму-
лу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.
Геометрический смысл определенного интеграла заключается в следующем: оп-
ределенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Физический смысл определенного интеграла состоит в следующем. Работа пе-
JG
ременной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [a; b].
ФОРМУЛА ПРЯМОУГОЛЬНИКОВ
Пусть на отрезке [a;b], a < b, задана непрерывная функция f (x). Требуется вычислить интеграл
b
∫ f (x)dx , численно равные пло-
a
щади соответствующей криволинейной трапеции. Разобьем основание этой трапеции, т.е. отрезок [a;b], на n равных частей (отрезков) длины
h = b −a = xi − xi−1 (шаг разбиения) (шаг разбиения) с помощью точек xo = a, x1, x2, …, xnn = b. Можно записать, что
xi = xo + h i, где i = 1, 2, …,n.
В середине ci = xi−12+ xi каждого такого отрезка построим ординату yi = f (ci) гра-
фика функции y = f (x). Приняв эту ординату за высоту, построим прямоугольник с площадью h yi.
2

Тогда сумма площадей всех n прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла
b |
|
b −a |
n |
xi−1 + xi |
|
|||
|
|
|
||||||
∫ f (x)dx ≈h( y1 + y2 |
+... + yn ) = |
|
∑f |
|
|
(1) |
||
n |
2 |
|||||||
a |
|
i=1 |
|
|
|
|||
Формула (1) называется формулой средних прямоугольников.
Абсолютная погрешность приближенного равенства оценивается с помощью следующей формулы:
(b −a)2 M1
2n
где M1 – наибольшее значение | f ′(x)| на отрезке [a;b].
ФОРМУЛА ТРАПЕЦИЙ
Эту формулу получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Разобьем отрезок [a;b] на n рав-
ных частей длины h = b −n a . Абс-
циссы точек деления a = xo, x1, x2,
…, b = xn. Пусть yo, y1,…, yn –
соответствующие им ординаты графика функции. Тогда расчетные формулы для этих значений
примут вид
xi = a + h i, yi = f (xi), i = 0,1,2,…,n; h = b −n a .
Заменим кривую y = f (x) ломаной линией, звенья которой соединяют концы ординат yi и yi + 1 (i = 0,1,2,…,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями yi, yi + 1 и высотой
h = |
b −a |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
yo + y1 |
|
|
y1 + y2 |
|
|
|
yn−1 + yn |
|
||
|
|
|
∫ f (x)dx |
≈ |
|
h + |
|
h +... + |
h |
||||||||
|
|
|
|
|
|
|
|||||||||||
или |
|
a |
|
|
2 |
|
2 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
b −a |
yo + yn |
|
|
|
|
|
|
|
|
|
|
|||
|
∫ f (x)dx ≈ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ y1 + y2 |
+... + yn−1 |
(2) |
|
|
|||||||
|
2 |
|
2 |
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формула (2) называется формулой трапеций.
Абсолютная погрешность приближения, полученного по формуле трапеций, оценивается с помощью формулы
3

(b −a)3 M2 , 12n2
где M2 – наибольшее значение | f ′′(x)| на отрезке [a;b].
ФОРМУЛА ПАРАБОЛ (СИМПСОНА)
Если заменить график функции y = f (x) на каждом отрезке [xi–1; xi] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла.
Предварительно найдем площадь S криволинейной трапеции, ограниченной сверху графиком параболы y = ax2 + bx + c, сбоку – прямыми x = –h, x = h и снизу – отрезком [–h; h].
Пусть парабола проходит через три точки M1(–h;yo), M2(0;y1), M3(h;y3), где yo = ah2 – bh + c – ордината параболы в точке x = –
h; y1 = c – ордината параболы в точке x = h. Площадь S равна
h |
|
x |
3 |
|
x |
2 |
|
|
h |
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
S = ∫ |
(ax2 +bx +c)dx = a |
|
+b |
|
+cx |
|
|
= |
ah3 |
+2ch . (3) |
|||
|
|
|
|
|
|
|
|||||||
−h |
|
3 |
2 |
|
|
−h |
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Выразим эту площадь через h, yo, y1, y2. Из равенств для ординат yi находим, что
c = y1, a = |
|
1 |
( y |
−2 y + y |
|
) . Подставим эти значения в равенство (3), получаем |
||||||||||||||
|
|
2 |
||||||||||||||||||
|
|
|
|
2h2 |
|
o |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
1 |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||
S = |
h3 |
|
( y |
|
−2 y + y |
|
) +2hy |
= |
( y |
|
+4 y + y |
|
) . (4) |
|
||||||
|
|
|
o |
2 |
|
o |
2 |
|
||||||||||||
3 |
|
2h2 |
|
|
1 |
|
|
1 |
3 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим теперь |
формул для |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычисления |
интеграла |
b
∫ f (x)dx .
a
Для этого отрезок [a;b] разобьем на 2n равных частей (от-
резков) длиной h = b2−na точка-
ми xi = xo + ih (i = 0,1,2,…,2n).
В точках деления
a = xo, x1, x2, …, x2n–2, x2n–1, x2n = b
вычисляем значения подынтегральной функции f (x):
yo, y1, y2, …, y2n–2, y2n–1, y2n,
где yi = f (xi).
Заменяем каждую пару элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапеции с основанием, равным
2h. На отрезке [xo;x2] парабола проходит через три точки (xo;yo), (x1;y1), (x2;y2). Используя формулу (4), находим
4

|
|
|
|
|
|
|
x |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
S1 = ∫2 |
f (x)dx = |
|
( yo + |
4 y1 + y2 ) . |
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
xo |
3 |
|
|
|
||||||
Аналогично находим |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|||
|
|
|
|
S2 = ∫4 |
f (x)dx = |
( y2 +4 y3 + y4 ),..., |
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x2 |
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
|
|
h |
|
|
|
|
|
|
|||
|
|
|
S2 |
= ∫2 n |
f (x)dx = |
( y2n−2 + |
4 y2n−1 + y2n ). |
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
x2 n−2 |
|
3 |
|
|
|
|
|
|
|||||
|
Сложив полученные равенства, имеем |
|
|
||||||||||||||
|
|
|
b |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx ≈ |
( yo +4 y1 + y2 + |
... +2 y2n−2 +4 y2n−1 + y2n ) |
||||||||||||
|
|
|
|
||||||||||||||
или |
a |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
b −a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx ≈ |
(( yo + y2n ) +4( y1 + y3 +... + y2n−1 ) + |
|
|||||||||||||||
6n |
(5) |
||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+2( y2 + y4 +... + y2n−2 ))
Формула (5) называется формулой парабол (или Симпсона).
Заметим, что для формулы Симпсона необходимо отрезок интегрирования разбивать на четное количество частей.
Абсолютная погрешность вычисления по формуле (5) оценивается соотношением
| Rn |≤ (b −a)5 M4 , 180(2n)4
где M4 = max | f IV (x) |.
a≤x≤b
b
Задача. Вычислить определенный интеграл ∫ f (x)dx по формулам средних пря-
a
моугольников, трапеций и Симпсона. Отрезок интегрирования разбить на n частей. Оценить абсолютную погрешность вычислений по каждой из формул.
Отчет по лабораторной работе должен содержать следующие материалы: 1) постановка задачи; 2) необходимый теоретический материал (краткий конспект); 3) решение поставленной задачи с использованием пакета Mathcad; 4) анализ полученных результатов.
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ
N |
|
|
f (x) |
n |
a |
B |
||
вари- |
|
|
||||||
анта |
|
|
|
|
|
|
|
|
1 |
|
|
sin x |
|
8 |
π |
π |
|
|
|
x |
6 |
3 |
||||
|
|
|
|
|||||
2 |
|
cos x |
|
10 |
π |
π |
||
|
|
x |
6 |
4 |
||||
|
|
|
|
|||||
5
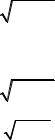
3 |
|
|
|
e−x |
|
10 |
2 |
4 |
|
|
|
|
x |
||||||
|
|
|
|
|
|
|
|||
4 |
|
arctg x |
|
10 |
1 |
1,5 |
|||
|
|
|
x |
||||||
|
|
|
|
|
|
|
|||
5 |
|
cos x2 |
10 |
0 |
π |
||||
|
6 |
||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
sin x2 |
10 |
0 |
π |
||||
|
6 |
||||||||
|
|
|
|
|
|
|
|
|
|
7 |
|
|
e−x2 |
20 |
0 |
1 |
|||
8 |
ln (1 + x2) |
10 |
0 |
1 |
|||||
9 |
3 1+ x2 |
10 |
0 |
1 |
|||||
10 |
|
x 23x |
20 |
1 |
1,8 |
||||
11 |
xln (1 + x) |
10 |
1 |
1,8 |
|||||
12 |
|
1+ x5 |
10 |
0 |
1 |
||||
13 |
|
|
|
sin x |
6 |
π |
π |
||
|
|
|
4 |
4 |
|||||
|
|
|
|
|
|
|
|
||
14 |
|
1 |
|
|
10 |
2 |
3 |
||
|
|
ln x |
|||||||
|
|
|
|
|
|
||||
15 |
|
|
e−x2 |
10 |
1 |
1,5 |
|||
Вопросы к защите лабораторной работы
1.Что называется определенным интегралом?
2.Что называют интегральной суммой?
3.Когда применяют формулу Ньютона-Лейбница?
4.Когда применяют численное интегрирование?
5.В чем заключается геометрический смысл определённого интеграла?
6.В чем заключается физический смысл определенного интеграла?
7.Вывод формулы прямоугольников.
8.Вывод формулы трапеций.
6
