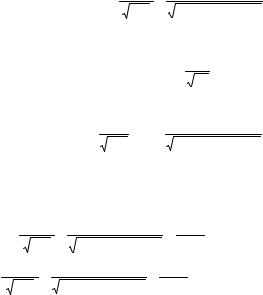
ряющее этому двойному неравенству m0 = 8, P10(8) ≈0,2718. Этому значению m соответствует наибольшее значение вероятности P10(m).

Пример 13. Статистическая вероятность рождения мальчика равна 0,515. В первые классы должно быть принято 200 детей. а) Найти наивероятнейшее число мальчиков, принимаемых школой в первый класс, и соответствующую этому событию вероятность; б) Найти вероятность того, что будет принято не более 100 мальчиков.

Решение. Условие задачи можно рассматривать как последовательность n = 200 независимых испытаний, в каждом из которых вероятность события A – {принятый в школу ребенок является мальчиком} постоянна и равна 0,515. То есть p = 0,515, q = 0,485.

а) Наивероятнейшее число наступлений события A в серии из n испытаний определяем по формуле np – q ≤m0 ≤np + p: 102,515 ≤m0 ≤103,515, значит, m0 = 103. Так как число испытаний n = 200 очень велико, то для определения P200(103), то есть вероятности того, что среди принимаемых школой детей окажется ровно 103 мальчика, можно воспользоваться локальной теоремой Лапласа, где

б) Вероятность события B – {в первые классы будет принято не более 100 мальчиков} можно определить с помощью интегральной теоремы Лапласа

P(B) = P200 (0 ≤ m ≤100) = Φ(x2 ) −Φ(x1) ,

Учитывая, что функция Φ(x) – нечетная, по таблицам значений функции Лапласа

Φ(x) находим: Φ(– 0,4244) = – 0,1628; Φ(– 14,5727) = – 0,5. Таким образом, P(B) = P(0 ≤m ≤100) = – 0,1628 + 0,5 = 0,3372.

21

2 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

2.1 Дискретные и непрерывные случайные величины

Как показывает практика, результаты вероятностного эксперимента в общем случае могут быть описаны одним или несколькими числами. То, какие именно числовые значения будут получены в результате эксперимента, зависит от большого числа не поддающихся учету случайных факторов и определяется реализовавшимся в результате вероятностного эксперимента элементарным исходом ωi .

Случайной величиной называется величина определенного физического смысла, значения которой подвержены некоторому неконтролируемому разбросу при повторениях исследуемого вероятностного эксперимента. Можно также сказать, что случайная величина – это функция, определенная на данном пространстве элементарных событий и ставящая в соответствие каждому элементарному событию ωi Ω некоторое вещественное число x.

Пример. Пусть производится подбрасывание монеты. Для описания результатов этого эксперимента можно рассмотреть элементарные события: ω1 – {выпадение цифры} и ω2 – {выпадение герба}, Ω = {ω1, ω2}. Поставив в соответствие исходу ω1 значение 0, а исходу ω2 – значение 1, получим описание результатов данного опыта с помощью случайной величины X, характеризующей число выпавших гербов, и принимающей в зависимости от исхода испытания одно из двух значений: 0 или 1.

В примере 1 (п. 1.1.1) рассматривался эксперимент, состоящий в подбрасывании игральной кости. Было построено пространство элементарных исходов, соответствующее этому испытанию: Ω= {ω1, ω2, ω3, ω4, ω5, ω6}. Каждому исходу ωi поставим в соответствие значение xi = i, (i = 1, 2,…, 6). Таким образом, ввели в рассмотрение случайную величину X, задающую число очков, выпавших на верхней грани, и принимающую в результате опыта одно из шести возможных значений.

Пример 5 (п. 1.1.2) Испытание состоит в трехкратном подбрасывании монеты. Результаты данного эксперимента могут быть описаны с помощью случайной величины X, определяющей число выпавших гербов. Возможные значения этой случайной величины: 0, 1, 2, 3.

Случайные величины принято обозначать прописными буквами латинского алфавита: X, Y, Z,…, либо буквами греческого алфавита: ξ, η, θ,…, а их значения – строчными буквами латинского алфавита: x, y, z.

Случайные величины, принимающие отдельные друг от друга значения с определенными вероятностями, называются дискретными. Множество возможных значений дискретных случайных величин является конечным или счетным множеством.

Примеры дискретных случайных величин: число успешно сданных экза-

22