54. Корректирующие коды как средство борьбы с ошибками. Циклические коды, их кодеры и декодеры.

Корректирующие коды позволяют исправлять ошибки. В зависимости от метода декодирования позволяют также обнаруживать и локализовывать ошибки. Корректирующие коды в зависимости от принципов их построе­ния подразделяют на: блочные и непрерывные. В блочных кодах последовательности символов разбивают на отдельные блоки с определеным числом элементов в них. Бло-чные коды, у которых кодовые комбинации имеют одну и ту же длину (число символов), называют равно-мерными, а коды с блоками различной длины - неравномерными. Непрерывные коды представляют собой непрерывную после­довательность символов, не подразделяемую на отдельные блоки. Блочные и непрерыв-ные коды делят на разделимые и неразделимые. В разделимых кодах для информационных и проверочных сим­волов отведены определенные позиции в кодовых последовательностях. Неразделимые коды не имеют закрепленных позиций за ин­формационными и проверочными символами. В корректирующем коде в отли-чие от простого для передачи ин­формации применяют не все множество кодовых комбинации So, a только его часть, образующую подмножество разрешенных комбина­ций Sp. Комбинации оставшегося подмноже-ства Sз = So - Sp для пере­дачи информации не используют и называют запрещенными. В простых кодах все комбинации являются разрешенными и ошиб­ки любой кратности вызывают переход одной комбинации в другую, также разрешенную, т.e. используемую для передачи информации. Поэтому ошибки в простом коде всегда приводят к неправильному приему информации. В корректирующих кодах вследствие того, что для передачи информации применяют только разрешенные комбинации Sp < So, возможно обнаруживать и исправлять ошибки. Одной из основных количественных хар-тик корректирующе­го кода является коэф-нт избыточности, характеризующий «цену» обнаружения или исправления ошибок: R = l - (log ₂ Sp / log ₂ So). Для блочных разделимых кодов, в которых k из п символов кодо­вых комбинаций являются информацион-ными, а остальные г - про­верочными, коэф-нт избыточности R = 1 - (k / n) = r / n. Избыточность в коректиру-ющих кодах снижает скорость передачи информации, что является существенным недостатком этих кодов. Однако их применение позволяет значительно повысить верность передачи. Корректирующая способность кода, т.e. его возможность обнару­живать и исправлять ошибки, зависит от того, насколько разрешен­ные комбинации отличаются друг от друга и от запрещенных. Мерой удаленности одной комбинации от другой является кодо­вое расстояние Хэмминга d, равное числу позиций, в кото­рых две кодовые комбинации одина-ковой длины отличаются друг от друга. Корректирующий код характе­ризуется минимальным кодовым рас-стоянием dmin. В простом коде dmin = 1 и ошибки любой кратности вызывают переход одной разре­шенной комбинаци в другую, также разрешеную, и ошибки обнаружить невозможно. Если в коде dmin = 2, то одно-кратные ошибки будут обнаружи­ваться, так как любая разрешенная комбинация будет переходить в запре-щенную. В общем случае для корректирующего кода, обнаруживающего все варианты ошибок кратности до δ включительно, необходимо и достаточ­но, чтобы dmin ≥δ + l. Наиболее общая идея исправления ошибок состоит в отождествле­нии принятой комбинации с ближней от нее разрешеной комбинацией. Для исправле-ния всех вариантов ошибок кратности до σ включительно необходимо dmin = 2σ + l. Коректирующие коды большой избыточности имеют обычно и высокую корректирующую способность.

Циклические коды являются разновидностью систематических кодов и обладают всеми их свойствами. В коде на подгруппу разрешенных кодовых комбинаций, помимо условия замкнутости по отношению к операции сложения, накладывается также ограничение по отношению к операции умножения (циклического сдвига символов кодовых комбинаций на одну позицию вправо или влево).

При построении циклических кодов кодовые комбинации принято представлять в виде многочленов переменной x:

P(x)=a_n-1x^n-1 + a_n-2x^n-2 + … + a₁x + a₀,

где a_n-1, …, a₁, a₀ – коэффициенты, принимающие значения 0 или 1.

Основное свойство рассматриваемых кодов состоит в том, что циклический сдвиг разрешенной кодовой комбинации также является разрешенной кодовой комбинацией. Циклический сдвиг эквивалентен умножению на х кодовой комбинации, записанной в виде многочлена:

xP(x) = a_n-1xⁿ + a_n-2x^n-1 + … + a₁x² + a₀x.

Так как в кодовой комбинации, имеющей длину n, степень многочлена не может превышать n – 1, то следует принимать xⁿ = 1. Тогда окончательный результат циклического сдвига многочлена на одну позицию влево будет

xP(x) = a_n-2x^n-1 + … + a₁x² + a₀x + a_n-1.

Принцип построения кодовых комбинаций циклических кодов заключается в следующем. Умножим каждую кодовую комбинацию А(х) простого k-символьного кода на х^r, где r = n – k, а затем разделим на порождающий (образующий) многочлен q(х) степени r. В результате умножения А(х) на х^r степень каждого слагаемого х_i, входящего в многочлен А(х), повышается на r. При делении произведения х^rА(х) на q(х) получим частное Q(х) такой же степени, что и А(х). Если произведение х^rА(х) не делится нацело на q(х), то получим остаток R(х):

x^rA(x)/q(x) = Q(x) + R(x)/q(x).

Поскольку частное Q(х) имеет ту же степень, что и A(x), то оно также является кодовой комбинацией простого k-символьного кода. Умножая обе части равенства на q(х), после переноса влево произведения Q(х) q(х) получим

F(х) = Q(х)q(х) = х^rА(х) + R(х).

Таким образом, кодовая комбинация циклического кода может быть получена двумя способами:

1) неразделимый код – умножением k-символьной кодовой комбинации простого кода на образующий многочлен q(х);

2) разделимый код – умножением кодовой комбинации простого кода на одночлен х^r и добавлением к этому произведению остатка от деления произведения х^rА(х) на q(х).

Неразделимость кода значительно усложняет процесс декодирования, поэтому на практике используется второй способ построения кодовых комбинаций.

В соответствии с принципом построения циклического кода в основе схем кодирования и декодирования лежат регистры сдвига, выполняющие операции умножения и деления многочленов. В лабораторной работе рассмотрены кодирующие и декодирующие устройства на следующие виды порождающих многочленов: q₁(x) = x⁴ + x+ 1

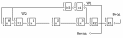
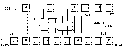
Из схем видно, что в состав кодера входят r-триггерный регистр сдвига, три ключа (К1, К2, К3) и двухвходовые сумматоры по модулю 2 (w), причем их число на единицу меньше числа ненулевых членов образующего многочлена q(х). Структура логических обратных связей в регистре сдвига, число элементов которого равно степени образующего многочлена, полностью определяется видом порождающего многочлена.

Сумматоры w₁,…,w_r-1 присутствуют в схеме в том случае, если соответствующие коэффициенты образующего многочлена а₁, …, а_r-1 равны 1.

Схема кодирующего устройства циклического кода работает следующим образом. Сначала ключ К2 закрыт, а ключи К1 и К3 открыты. Информационный многочлен A(x) поступает одновременно на выход кодера, начиная со старшего члена (идет умножение на одночлен х^r) и сумматор w₁. В процессе ее прохождения за k тактовых импульсов в ячейках регистра сдвига накапливается r проверочных символов (осуществляется деление х^rА(х) на образующий многочлен q(х)). После k-го тактового импульса ключи К1 и К3 закрываются, а К2 открывается. Далее полученные проверочные символы r тактовыми импульсами поступают на выход кодера.

Принцип действия кодера (рисунок 30) на примере информационной кодовой комбинации А(х) = х⁴ + х² + 1 = 10101, показан в таблице 7.

Закодированная кодовая комбинация запишется следующим образом:

F(х) = х⁸ + х⁶ + х⁴ + х³ + х = 101011010.

 

х^rА(х) R(х)

Таблица 7

Признаком, указывающим на наличие ошибки в принятой комбинации, служит остаток, получаемый в результате деления принятого многочлена F’(х) на образующий многочлен q(х).

Так как F’(х) = F(х)  Е(х), то F’(х)/q(х) = [F(х)  Е(х)]/q(х) = F(х)/q(x)  Е(х)/q(х). Так как F(х) делиться на q(х) без остатка, то неделимость F’(х) на q(х) определяется тем, что Е(х) не делиться на q(х). Таким образом, деление принятой комбинации с ошибкой F’(х) на образующий многочлен q(х) можно заменить делением многочлена ошибки Е(х) на этот многочлен.

На рисунке 31 приведена структурная схема декодирующего уст­ройства с порождающим многочленом вида q₁(х) = х⁴ + х + 1 с обнаружением и исправлением ошибок. В состав декодера входят: DS1 – буферный регистр, служащий для хранения принимаемой информации до ее исправления; DS2 – декодирующий регистр, служащий для обнаружения ошибки; DS – дешифратор синдрома, служащий для опознавания синдрома; HL – сигнализация ошибки.

Принимаемая кодовая комбинация с ошибкой декодируется с целью оп определения ошибки в комбинации. Если в полученном от деления на образующий многочлен q(x) остатке имеется хотя бы одна единица, т. е. он является ненулевым, то будет зафиксирована ошибка.

Дешифратор синдрома строится с таким расчетом, чтобы момент появления “1” на его выходе совпал с моментом прохождения ошибочного символа через сумматор w₁, включённый на выходе буферного регистра, в результате чего произойдет его исправление. Последовательность работы декодера при исправлении ошибки в четвертом символе принятой комбинации показана в таблице 8.

На 9-м тактовом импульсе в элементах памяти декодирующего регистра завершается формирование комбинации синдрома. Комбинация синдрома (жирные цифры) отлична от нуля, что свидетельствует о наличии ошибки.

Далее в буферный и декодирующий регистры подаются еще k (k = 5) тактовых импульсов, которые, во-первых, считывают информационные символы с буферного регистра через сумматор w₁ в приемник, а во-вторых, переформируют информацию в элементах декодирующего регистра.

Как видно из таблицы 8, на 12-м тактовом импульсе в элементах декодирующего регистра сформирована комбинация 0101, она поступает на вход дешифратора синдрома, на выходе которого возникает сигнал “1”.

Таблица8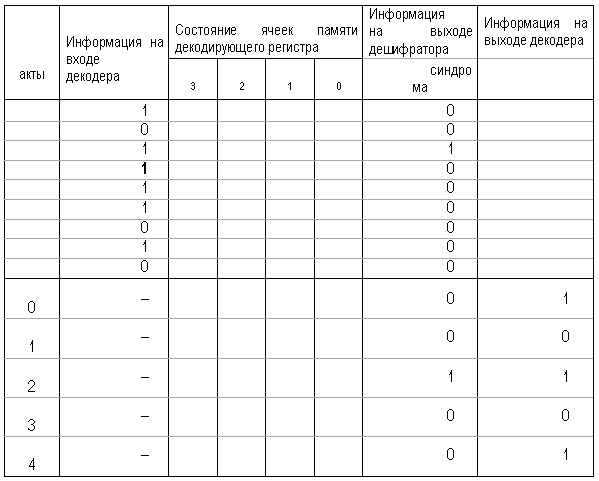В этот же момент времени на сумматор w₁ поступает искаженный 4-й информационный символ, который, проходя через сумматор, меняет знак на противоположный. Исправленная комбинация будет иметь вид: 10101.