
- •Математическое моделирование Учебное пособие
- •Донецк 2006
- •Содержание
- •Введение
- •1. Построение экспериментальных законов распределения
- •1.1. Общие положения
- •1.2. Статистические критерии согласия
- •Г) Критерий согласия Романовского
- •1.3. Построение закона Пуассона
- •1.4. Построение показательного закона
- •1.5. Построение нормального закона
- •2. Модели оптимизации
- •2.1. Принципы формирования моделей оптимизации
- •Задача производственного планирования
- •Задача оптимальной загрузки оборудования
- •Задача о смесях
- •Транспортная задача
- •2.2. Графический метод решения задачи линейного программирования
- •Алгоритм графического метода решения злп
- •2.3. Универсальный метод решения линейных задач оптимизации
- •Алгоритм симплекс-метода решения злп
- •Пример 2.3.1. Решить злп (2.2.1), (2.2.5) симплекс-методом.
- •Критерий оптимальности опорного плана
- •Переход к следующей симплекс-таблице осуществляют по правилам:
- •2.4. Двойственная задача линейного программирования
- •Свойства двойственных задач
- •2.5. Методы анализа конфликтных ситуаций с помощью матричных игр
- •Алгоритм принципа максимина (минимакса)
- •Решение. Этаматричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.
- •Последовательность действий при решении игры
- •3. Регрессионный анализ
- •3.1. Однофакторные модели
- •3.1.1. Построение однофакторных моделей
- •3.1.2. Оценка качества моделей
- •Свойства коэффициента корреляции
- •Построение доверительного интервала для прогнозного значения
- •Пример 3.1.Исследовать зависимость объема прибыли от количества торговых точек. Сделать прогноз в предположении, что количество торговых точек будет увеличено до 25.
- •Вспомогательная расчетная таблица
- •Пример 3.2.Исследовать зависимость показателяуи факторахс помощью логарифмической, степенной и полиномиальной регрессий.
- •3.1.3. Модели рядов динамики
- •3.2. Автокорреляция данных и остатков
- •3.2.1. Автокорреляция данных
- •Пример 3.4. Исследовать на автокорреляцию динамический ряд:
- •Вспомогательная таблица для расчета коэффициента автокорреляции
- •3.2.2. Автокорреляция остатков
- •Причины возникновения автокорреляции
- •Вспомогательная таблица для расчета d-статистики
- •С помощью формулы (3.2.2) найдем d -статистику:
- •3.3. Мультиколлинеарность
- •Причины возникновения мультиколлинеарности:
- •Методы исследования мультиколлинеарности
- •Меры по устранению мультиколлинеарности:
- •3.4. Множественная линейная регрессия
- •3.4.1. Построение множественной линейной регрессии
- •Расчет элементов коэффициента
- •3.4.2. Матричный подход
- •Построение корреляционной матрицы
- •Построение модели множественной линейной регрессии и ее анализ
- •3.4.4. Нелинейные модели
- •3.4.5. Эластичность
- •4.Экспертные оценки и элементы теории графов
- •4.1. Ранговая корреляция
- •4.1.1. Экспертное оценивание
- •4.1.2. Этапы работ в системе экспертных оценок
- •4.1.3. Метод ранговой корреляции
- •Вспомогательные расчеты
- •Б) Случай многих экспертов
- •4.2. Элементы сетевого планирования
- •Основные элементы сетевого графика
- •Основные требования к сетевой модели
- •5. Индивидуальные задания для самостоятельной работы студентов по курсу “математическое моделирование”
- •5.1. Задания к разделу “Построение законов распределения”
- •5.2. Задания к разделу “Математическое программирование”
- •5.3. Задания к разделу “Регрессионный анализ”
- •Задание 2.
- •Задание 3.
- •5.4. Задания к разделу “Экспертные оценки и элементы теории графов” Задание 1.
- •Значение критерия Пирсона
- •Критерий Колмогорова
- •Критерий Колмогорова
- •Квантили распределения Стьюдента
- •Коефициентов автокорреляции
- •Литература
- •Пеніна Галина Геннадіївна, канд. Екон. Наук, доцент
1.2. Статистические критерии согласия
В результате наблюдений получено
эмпирическое распределение величины
Хс частотами![]()
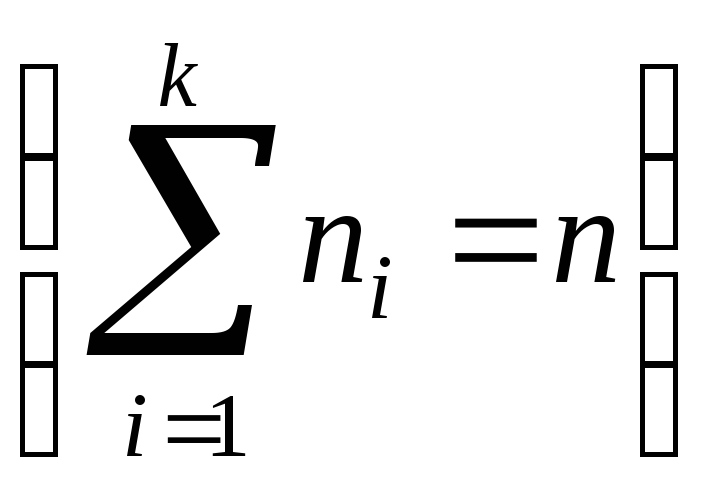 .
В результате выбора закона определены
теоретические частоты
.
В результате выбора закона определены
теоретические частоты![]() (k– число значений
или частичных интервалов).
(k– число значений
или частичных интервалов).
а) Критерий согласия Пирсона
![]()
За меру расхождения частот принимают величину:
![]() (1.2.1)
(1.2.1)
По уровню значимости
![]() =
0,05 (0,1; 0,01) и числу степеней свободы
=
0,05 (0,1; 0,01) и числу степеней свободы![]() в таблице Пирсона (приложение А) находят
в таблице Пирсона (приложение А) находят![]() .
Если
.
Если![]() ,
то гипотеза о законе не отвергается, он
может быть использован. Если же
,
то гипотеза о законе не отвергается, он
может быть использован. Если же![]() ,
то гипотеза о рассматриваемом законе
распределения отвергается.
,
то гипотеза о рассматриваемом законе
распределения отвергается.
б) Критерий согласия Колмогорова
По вариационному ряду составляют
эмпирическую функцию распределения
![]() .
Выбрав закон, формируют теоретическую
функцию
.
Выбрав закон, формируют теоретическую
функцию![]() ,
определяют максимальное отличие
,
определяют максимальное отличие![]() и получают характеристику Колмогорова
и получают характеристику Колмогорова
![]() .
(1.2.2)
.
(1.2.2)
Пользуясь специальными таблицами
(приложение Б), находят вероятность
![]() .
Если эта вероятность меньше 0,01, то
гипотезу о выбранном законе распределения
отвергают. Если вероятность больше (или
равна) 0,01, то расхождения между эмпирической
и теоретической функциями признают
несущественными, а гипотезу о выбранном
законе распределения вполне согласованной
с экспериментом.
.
Если эта вероятность меньше 0,01, то
гипотезу о выбранном законе распределения
отвергают. Если вероятность больше (или
равна) 0,01, то расхождения между эмпирической
и теоретической функциями признают
несущественными, а гипотезу о выбранном
законе распределения вполне согласованной
с экспериментом.
Замечание.Если![]() 0,29, то вероятность равна единице.
0,29, то вероятность равна единице.
в) Критерий согласия Ястремского
Известный статистик Б.С.Ястремский доказал, что меру близости теоретического и фактического распределений можно характеризовать величиной
![]() ,
(1.2.3)
,
(1.2.3)
где
![]() ,
,![]() ,
,![]() – теоретическая вероятность того, что
случайная величинаХ
примет значение
– теоретическая вероятность того, что
случайная величинаХ
примет значение
![]() ;k
– число групп;
;k
– число групп;
![]() при
при![]() .
.
Если
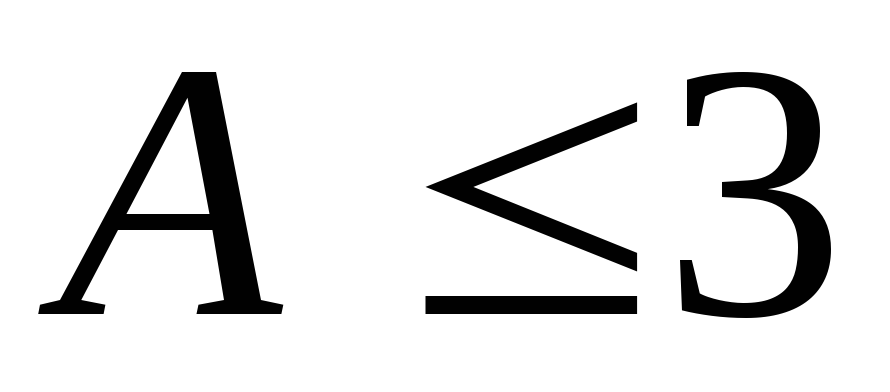 ,
то расхождение между теоретическим и
фактическим распределениями несущественно.
,
то расхождение между теоретическим и
фактическим распределениями несущественно.Если
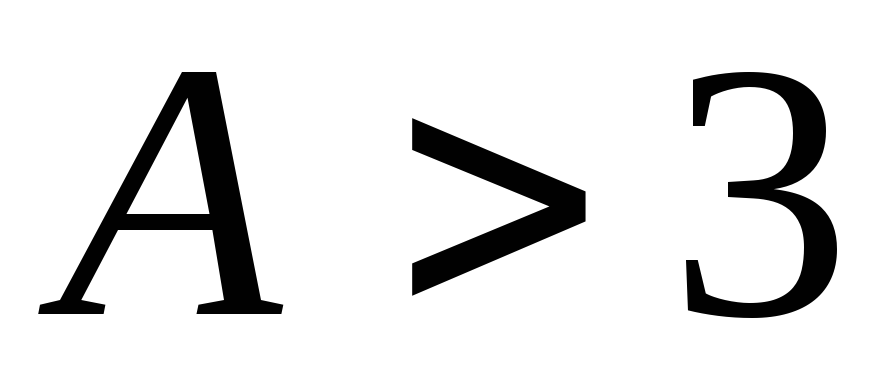 ,
то это расхождение существенно и его
невозможно объяснить влиянием случайных
факторов, поэтому теоретический закон
распределения следует отклонить.
,
то это расхождение существенно и его
невозможно объяснить влиянием случайных
факторов, поэтому теоретический закон
распределения следует отклонить.
Г) Критерий согласия Романовского
Этот критерий используется для оценки степени приближения эмпирического распределения к теоретическому. Он тесным образом связан с критерием согласия Пирсона и состоит в том, что вычисляют величину
![]() ,
(1.2.3)
,
(1.2.3)
где
![]() ,q
– число степеней свободы,
,q
– число степеней свободы,
![]() .
.
Если
![]() ,
то это означает, что результаты испытаний
не противоречат гипотезе о законе
распределения. В противном случае
гипотеза отвергается.
,
то это означает, что результаты испытаний
не противоречат гипотезе о законе
распределения. В противном случае
гипотеза отвергается.
Критерий В.И.Романовского является хорошим дополнением к критерию Пирсона.
1.3. Построение закона Пуассона
Этот закон используется во многих процессах, и в частности, в описании потока клиентов (заявок, требований) в системах массового обслуживания. Он описывает дискретные случайные величины, т.е. величины, которые могут принимать отдельные изолированные значения из некоторого интервала.
Предположим, что в результате наблюдений за случайной величиной получен дискретный вариационный ряд:
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
где
![]() – значения случайной величины,
– значения случайной величины,
![]() – частота соответствующих
– частота соответствующих![]() ,
,![]()
![]() .
.
Если предположить, что случайная величина, подчиняется закону Пуассона, то вероятности каждого значения должны определяться по формуле
![]() ,
(1.3.1)
,
(1.3.1)
где
![]() – параметр закона, совпадающий с
математическим ожиданием:
– параметр закона, совпадающий с
математическим ожиданием:
![]() .
.
Другими словами, чтобы сформировать закон, необходимо вычислить по опытным значениям математическое ожидание и подставить в формулу (1.3.1).
Определяя
для каждого значения
![]() вероятность
вероятность![]() ,
находят соответствующие теоретические
частоты:
,
находят соответствующие теоретические
частоты:
![]() .
.
Пример 1.1. Было проведено 200 наблюдений (каждое длилось 2 мин.), в результате отмечалось следующее распределение покупателей:
-
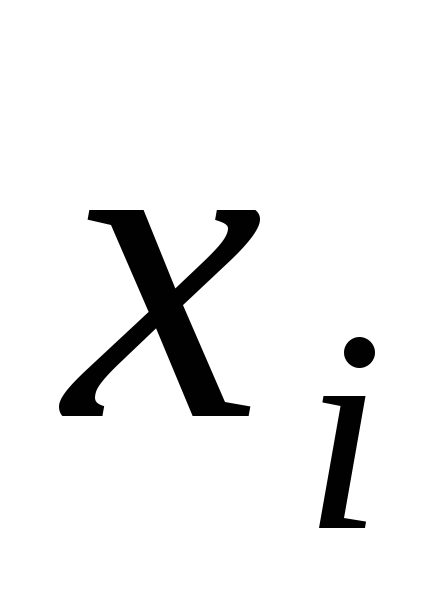
0
1
2
3
4
5
6
7
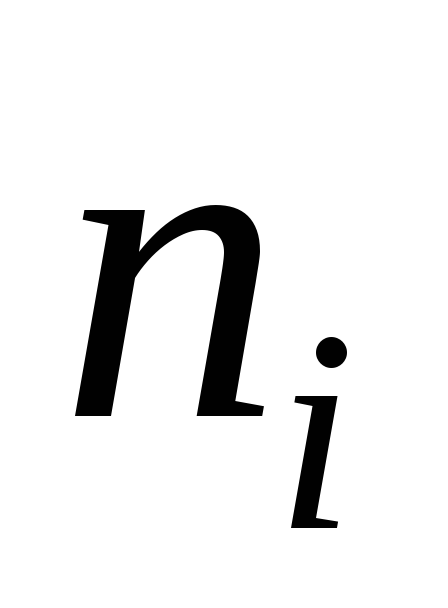
41
62
45
22
16
8
4
2
Проверить, можно ли описать этот поток с помощью закона Пуассона (является ли он простейшим)?
Решение. Определим среднее число заявок (клиентов):
![]() .
.
Сформируем функцию вероятностей Пуассона по формуле (1.3.1):
![]() .
.
а) Проверим по критерию
Пирсона, подходит ли этот закон. Для
этого каждому значению
![]() поставим в соответствие вероятность
поставим в соответствие вероятность![]() ,
определим
,
определим![]() и рассчитаем
и рассчитаем![]() :
:
![]() ,
,![]() ,
,![]() и т.д.
и т.д.
Все расчеты проведем в таблице 1.1.
Таблица 1.1
Проверка закона Пуассона по критерию Пирсона
|
|
|
|
|
|
|
|
0 |
41 |
0,1653 |
33 |
64 |
1,939 |
|
1 |
62 |
0,2975 |
60 |
4 |
0,067 |
|
2 |
45 |
0,2678 |
54 |
81 |
1,500 |
|
3 |
22 |
0,1607 |
32 |
100 |
3,125 |
|
4 |
16 |
0,0723 |
14 |
4 |
0,286 |
|
5 |
8 |
0,0260 |
5 |
9 |
1,800 |
|
6 |
4 |
0,0078 |
2 |
4 |
2,000 |
|
7 |
2 |
0,0026 |
0 |
4 |
2,000 |
|
|
200 |
1,0000 |
- |
- |
12,72 |
|
Замечание. |
Последнее
значение
|
Имеем![]() ,
,![]() ,
,![]() .
По таблицам Пирсона (приложение А)
находим
.
По таблицам Пирсона (приложение А)
находим![]() .
В результате
.
В результате![]() .
.
Вывод: расчетное и критическое
значения достаточно близки, т.к. расчетное
значение![]() все же больше критического, то возможность
применения закона сомнительна.
все же больше критического, то возможность
применения закона сомнительна.
б) Проверим по критерию Колмогорова.
Предварительно найдем фактические (![]() )
и теоретические вероятности (
)
и теоретические вероятности (![]() ),
затем сформируем эмпирическую (
),
затем сформируем эмпирическую (![]() )
и теоретическую (F)
функции распределения (таблица 1.2) и
найдем их разности.
)
и теоретическую (F)
функции распределения (таблица 1.2) и
найдем их разности.
Таблица 1.2
Проверка закона Пуассона по критерию Колмогорова
|
|
|
|
|
|
|
|
0 |
0,205 |
0 |
0,165 |
0 |
0 |
|
1 |
0,31 |
0,205 |
0,298 |
0,165 |
0,04 |
|
2 |
0,225 |
0,515 |
0,268 |
0,463 |
0,052 |
|
3 |
0,11 |
0,74 |
0,161 |
0,731 |
0,009 |
|
4 |
0,08 |
0,85 |
0,072 |
0,892 |
0,042 |
|
5 |
0,04 |
0,93 |
0,026 |
0,964 |
0,034 |
|
6 |
0,02 |
0,97 |
0,007 |
0,99 |
0,02 |
|
7 |
0,01 |
0,99 |
0,003 |
0,997 |
0,007 |
|
|
- |
1 |
- |
1 |
- |
По формуле (1.2.2) рассчитаем характеристику Колмогорова
![]() .
.
Вывод:вероятность![]() =1,
по данному критерию использование
закона вполне допустимо.
=1,
по данному критерию использование
закона вполне допустимо.
в) Оценим закон Пуассона по критерию Ястремского. Для нахождения величины Q, для чего построим вспомогательную расчетную таблицу 1.3.
Таблица 1.3
Вспомогательная расчетная таблица
|
|
|
|
|
|
|
41 |
33 |
0,165 |
0,835 |
2,323 |
|
62 |
60 |
0,298 |
0,702 |
0,095 |
|
45 |
54 |
0,268 |
0,732 |
2,049 |
|
22 |
32 |
0,161 |
0,839 |
3,725 |
|
16 |
14 |
0,072 |
0,928 |
0,308 |
|
8 |
5 |
0,026 |
0,974 |
1,848 |
|
4 |
2 |
0,007 |
0,993 |
2,014 |
|
2 |
0 |
0,003 |
0,997 |
2,006 |
|
|
|
|
|
14,368 |
Таким образом, Q=14,368. Посколькуk= 8,Z= 0,6, то по формуле (1.2.3) имеем:
А =![]() .
.
Вывод:посколькуА< 3, то по этому критерию гипотеза о законе принимается.
г) Проверим пригодность закона Пуассона по критерию согласия Романовского.
Поскольку
![]() = 12,72,q = 8 – 2 = 6, то
по формуле (1.2.3) имеем
= 12,72,q = 8 – 2 = 6, то
по формуле (1.2.3) имеем
![]() .
.
Вывод:величина![]() меньше 3 – значит, в соответствии с этим
критерием гипотеза о законе Пуассона
не отвергается.
меньше 3 – значит, в соответствии с этим
критерием гипотеза о законе Пуассона
не отвергается.
|
Замечание. |
В данном примере оказалось, что по трем критериям согласия из четырех закон Пуассона не отвергается. Следовательно, общий вывод состоит в возможности применения закона Пуассона к данному ряду. |
