3.4. Множественная линейная регрессия

3.4.1. Построение множественной линейной регрессии

Каждое явление в природе, технике, экономике, общественной жизни определяется комплексом причин. На уровень развития одного показателя могут влиять много факторов. Уровень влияния факторов на показатель может существенно различаться. Все эти закономерности следует учитывать во время проведения эконометрического анализа, прогнозирования и планирования.

При существовании линейной зависимости объясняемой переменной (показателя) от нескольких объясняющих переменных (факторов)общее выражение уравнения множественной регрессии имеет вид:

, (3.4.1)

где у – зависимая переменная, – независимые факторы,– параметры модели. Здесь через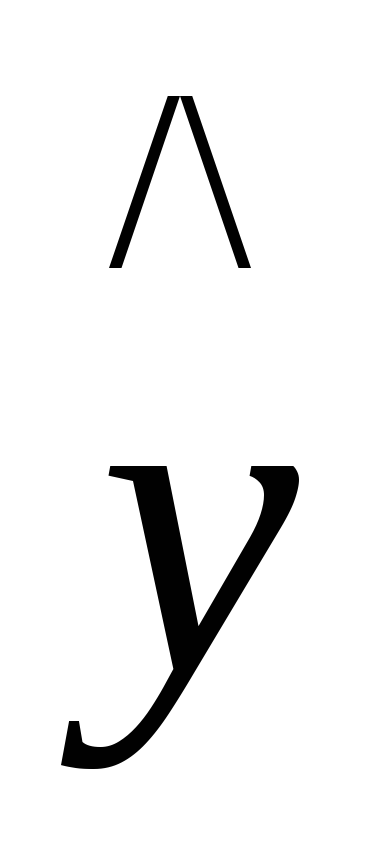обозначены теоретические значения показателя, рассчитываемые по модели (3.4.1).

Модель описывает совместное одновременное влияние факторов на показатель. Задача исследования состоит в оценке параметров регрессии по результатам выборочных наблюдений над переменными, которые включены в модель. Построение модели проводят с помощью метода наименьших квадратов, решая систему уравнений Гаусса (3.4.2):

(3.4.2)

Данную систему можно решать, используя ранее рассмотренный подход: вычислить все вспомогательные суммы, подставить их в систему и, преобразуя ее с помощью алгебраических преобразований, найти неизвестные параметры уравнения. Это так называемая классическая схема построения многофакторной модели.

Важным этапом регрессионного анализа является оценка практической значимости построенной модели. Проверку значимости модели проводят на основании показателей тесноты связи между признаками ис помощьюмножественного коэффициента корреляции, который выявляет зависимость между фактическими и теоретическими значениями объясняемой переменной. Его вычисляют по формуле (3.4.3)

(3.4.3)

Чем более близок множественный коэффициент корреляции к единице, тем лучше данная модель описывает фактические данные.

Коэффициент детерминацииравен квадрату множественного коэффициента корреляции. Он измеряет долю общей дисперсии относительно среднего, которую можно объяснить регрессией.

Полезным является построение интервальных границ для коэффициента множественной регрессии.

Доверительный интервал для множественного коэффициента корреляциинаходится по формуле (3.4.4)

, (3.4.4)

где ,

– критическая точка, найденная по таблицам Стьюдента (приложение Д).

Для проверки значимости уравнения регрессии применяюткритерий Фишера, вычисляя фактическое значение-статистики по формуле (3.4.5):

. (3.4.5)

По таблице критических точек Фишера (приложение Е) находят критическое значение статистики , где– количество наблюдений,– количество факторов,– уровень значимости.

Если , то уравнение регрессии не является надежно значимым. Если, то уравнение регрессии является значимым.

Прогноз. Предположим, что мы хотим распространить построенную модель на другие значения факторных переменных и решить проблему прогнозирования среднего значения, которое отвечает некоторым данным значениямпеременных. Эти новые значениямогут лежать как между выборочными наблюдениями, так и вне соответствующих интервалов. Точечный прогноз представляет собой вычисленное по уравнению (3.4.1) значение

. (3.4.6)

Пример 3.7. Построить линейную регрессионную модель по данным примера 3.6.

Решение.В примере 3.6 из дальнейшего рассмотрения была исключена переменная. Используем линейную двухфакторную модель

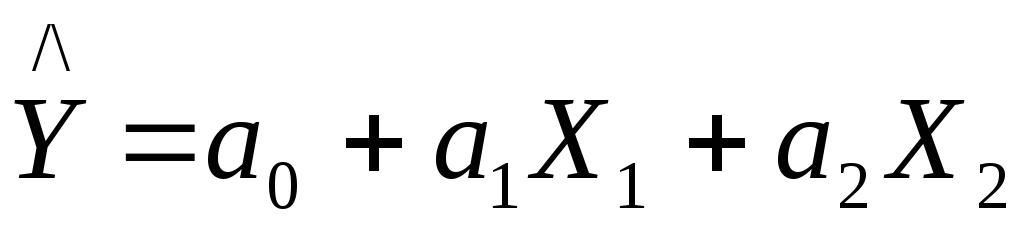, (3.4.6)

В соответствии с методом наименьших квадратов параметры найдем как решение системы линейных уравнений Гаусса следующего вида

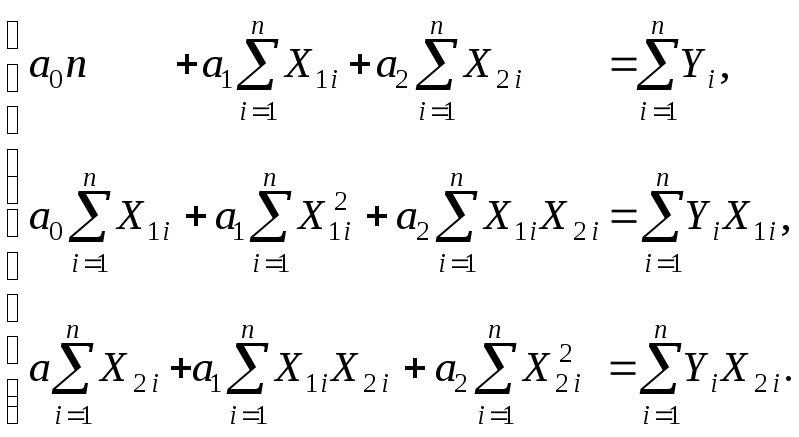(3.4.7)

Вспомогательные вычисления удобно проводить в таблице:

Таблица 3.13

Расчет коэффициентов системы (3.4.7)

17,44	22,95	3,00	526,70	9,00	68,85	400,25	52,32
17,28	24,84	1,56	617,03	2,43	38,75	429,24	26,96
17,92	29,97	2,88	898,20	8,29	86,31	537,06	51,61
18,88	28,08	2,28	788,49	5,20	64,02	530,15	43,05
17,12	24,30	1,20	590,49	1,44	29,16	416,02	20,54
21,12	32,40	2,64	1049,76	6,97	85,54	684,29	55,76
20,00	29,97	3,48	898,20	12,11	104,30	599,40	69,60
20,64	33,48	2,28	1120,91	5,20	76,33	691,03	47,06
19,68	29,70	2,52	882,09	6,35	74,84	584,50	49,59
18,40	26,73	2,40	714,49	5,76	64,15	491,83	44,16
188,48	282,42	24,24	8086,36	62,76	692,26	5363,76	460,65

В последней строке записывают суммы чисел в столбце.

Система уравнений (3.4.7) для определения параметров регрессии имеет вид:

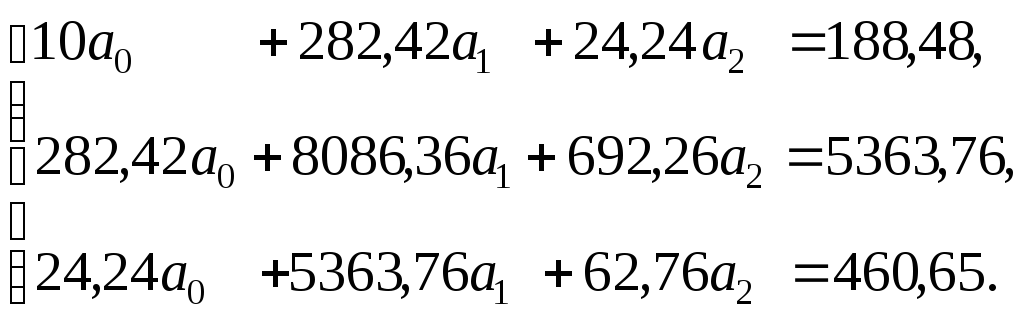
Решив полученную систему уравнений, найдем ,, тогда уравнение регрессии (3.4.6) имеет вид

. (3.4.8)

Пример 3.8. Для модели (3.4.8), построенной в примере 3.7, найти множественный коэффициент корреляции , коэффициент детерминации, для множественного коэффициента корреляциинайти доверительный интервал, коэффициенты эластичности.

Решение. Для вычисления множественного коэффициента корреляции построим вспомогательную таблицу:

Таблица 3.14