3. Регрессионный анализ

Изучение процессов и явлений разной природы связано с показателями, характеризующими различные стороны этих процессов. Рассматривая причинно-следственные связи, из множества причин выбирают наиболее существенные, освобождаясь от элементов случайности и действия второстепенных величин.

Вначале анализа явление должно быть проинтерпретировано с содержательной точки зрения. На основе логического анализа исследователь решает, какую из переменных рассматривать как зависимую (следствие, показатель), или переменную, подлежащую объяснению с помощью функции регрессии, и какие переменные в ходе анализа считать объясняющими (причины), независимыми или предсказывающими. Причины и следствие должны быть объяснены теорией.

На уровень развития одного показателя могут оказывать влияние множество факторов, степень влияния которых различна. Эти закономерности нужно учитывать при проведении анализа изучаемого процесса или явления, планировании и прогнозировании. Для изучения форм связи между показателем и факторами на основе статистических данных используется регрессионный анализ.

Задача регрессионного анализа состоит в установлении формы зависимости между переменными, оценке функции регрессии, прогнозе значений зависимой переменной.

3.1. Однофакторные модели

3.1.1. Построение однофакторных моделей

Линейной регрессией Y на Xназывается односторонняя стохастическая линейная зависимость между случайными величинами показателяY(объясняемой, зависимой переменной) и фактораX (объясняющей, независимой переменной), которая находятся в причинно-следственных отношениях.

Рассмотрим модель линейной регрессии. Допустим, что имеем результаты nпар независимых наблюдений, изображённых в виде множества точек в декартовой системе координат. Предположим, что между показателему и факторомх существует стохастическая линейная зависимость. Суть задачи состоит в том, чтобы в декартовой системе координат найти линию, которая “наилучшим” образом соответствует заданному множеству точек. В этом случае линейная парная регрессионная модель имеет вид

,

где у– зависимая переменная,х– объясняющая переменная,– возмущения (остатки) – величина случайная, которая характеризует влияние неучтенных факторов.

Классический регрессионный анализ оценок ипараметровиоснован на методе наименьших квадратов (основоположники – К.Гаусс, П.Лаплас).

Уравнение регрессии будем искать в виде линейного уравнения 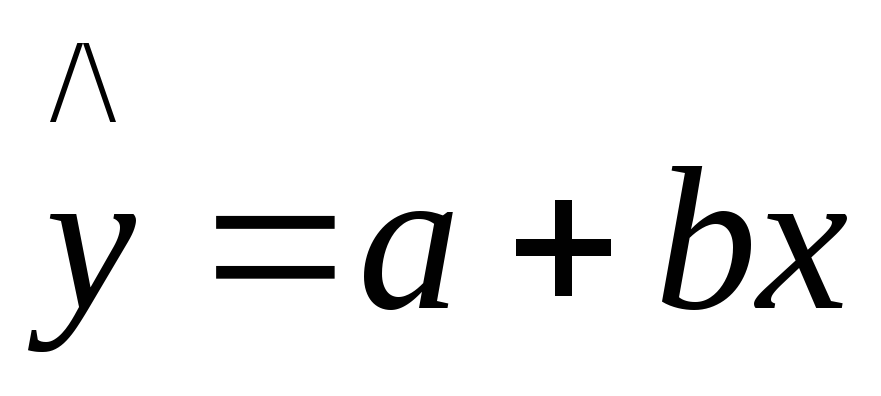(3.1.1):

. (3.1.1)

Зависимость (3.1.1), которая характеризует среднее значение показателя у для данного значения факторах, называетсярегрессией. Она характеризует тенденцию изменения показателя, обусловленную влиянием изменения фактора.

Для нахождения оценок параметров иприменяют метод наименьших квадратов. Для этого составляют систему линейных уравнений Гаусса:

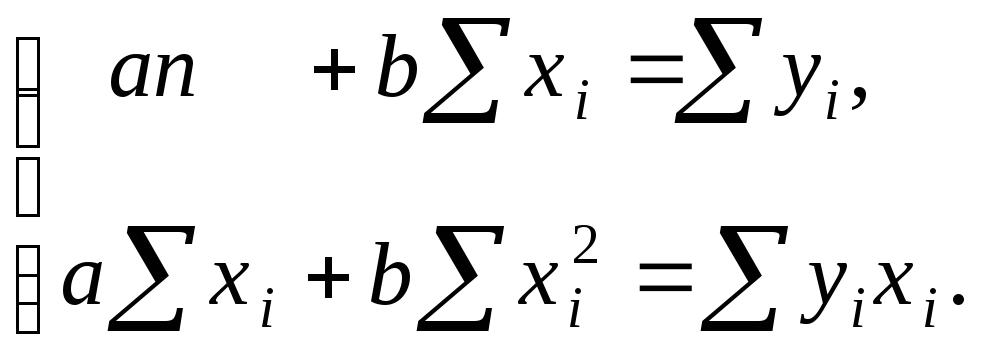(3.1.2)

Интерпретация оценок параметров уравнения прямой линии регрессии:

изменение величины фактора Xна единицу при прочих равных условиях вызовет изменение показателяYна количество единиц, равное значению. При нулевом уровне независимой переменной (фактора)Xвеличинаопределяет значение показателя.

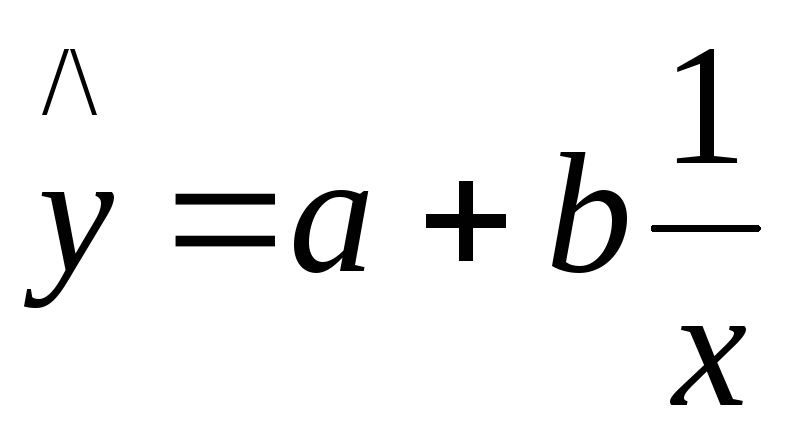Для выбора и обоснования типа кривой регрессии нет универсального метода. Для описания односторонней стохастической зависимости между явлениями чаще всего применяются полиномиальная регрессия: , гиперболическая регрессия:, степенная регрессия:. Применяются также показательная, экпоненциальная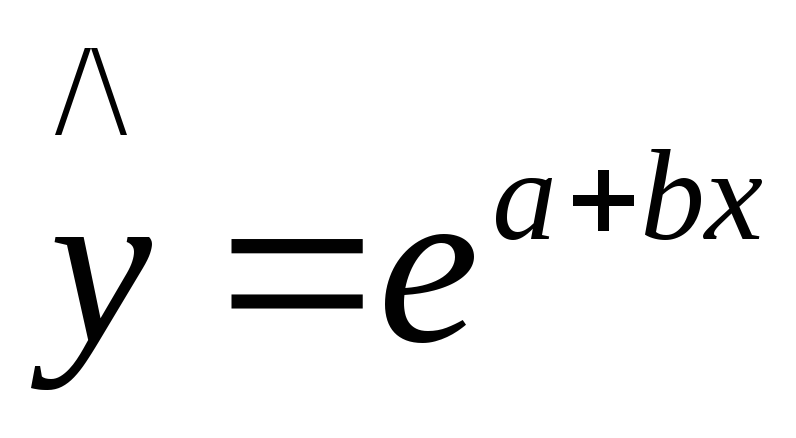, логарифмическая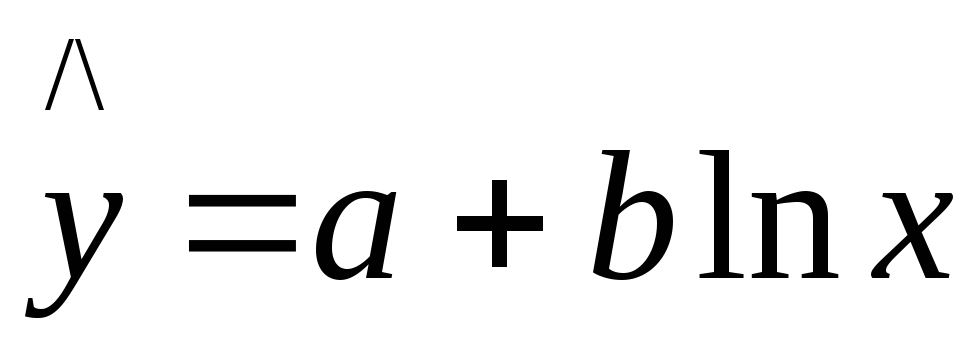и другие функции. О характере зависимости между экономическими явлениями часто судят по внешнему виду эмпирического графика регрессии. Однако при малом числе наблюдений этот путь приводит к неудовлетворительным результатам. В каждом случае следует проверять возможность применения линейной регрессии хотя бы на ограниченном участке изменения переменных.

Если показатель у при росте х состоит из двух частей – постоянной (не зависящей от х) и переменной (уменьшающейся с ростом х), то для описания зависимости у от х следует применить уравнение гиперболы.

Если показатель у отражает процесс, который под влияние фактора х происходит с ускорением (или замедлением), то применяются полиномы.

Если процесс вначале ускоренно развивается, а затем затухает и приближается к некоторому предельному значению, то можно применить логистическую функцию .

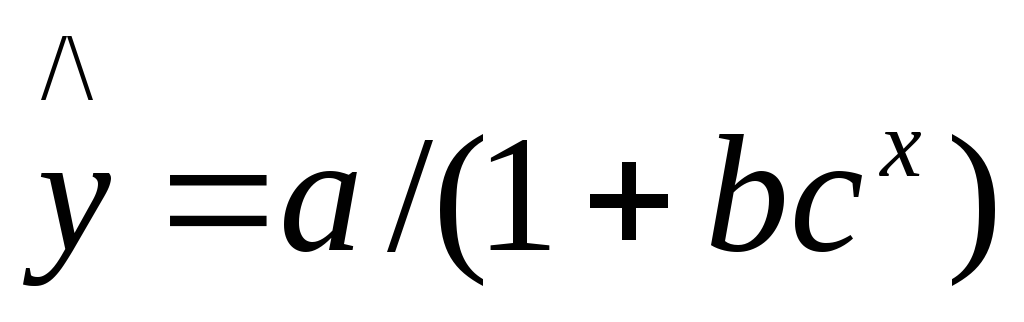Замечание.

Нелинейность связей в некоторых случаях может быть следствием качественной неоднородности изучаемой совокупности. Регрессионный анализ таких совокупностей не может быть эффективным. Поэтому любая нелинейность связей должна критически анализироваться.

Рассмотрим нелинейную регрессию в виде параболы второй степени

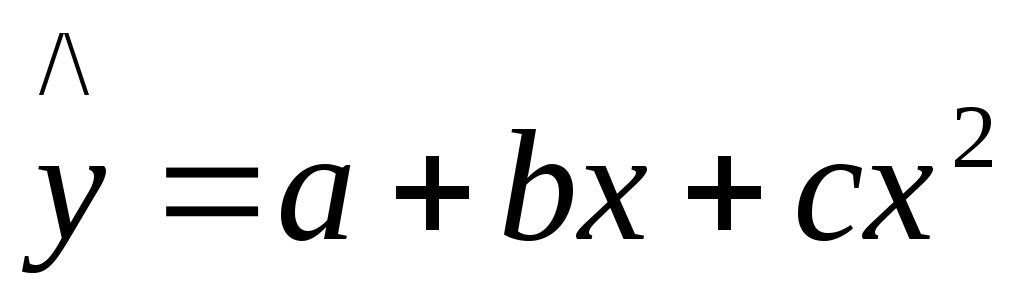. (3.1.2)

Оценку параметров уравнения (3.1.15) можно проводить с помощью метода наименьших квадратов, используя систему уравнений Гаусса:

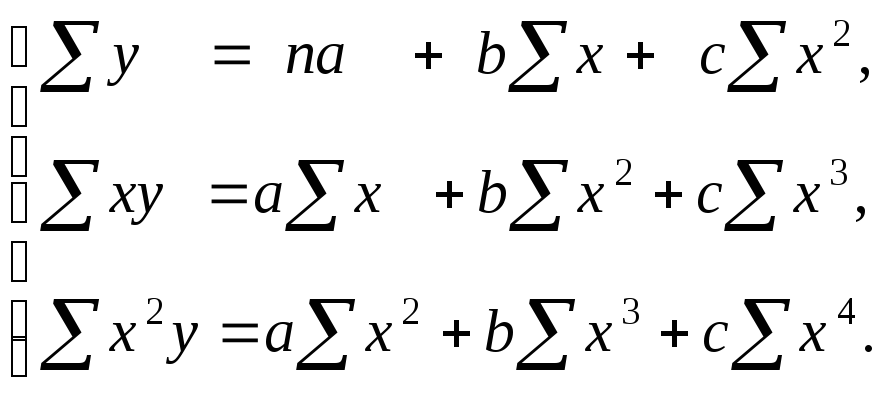(3.1.3)

Заменяя переменные ,, получим двухфакторное уравнение линейной регрессии:

,

для оценки параметров которого, используется метод наименьших квадратов, как будет показано в пункте 3.4.

В уравнении гиперболы 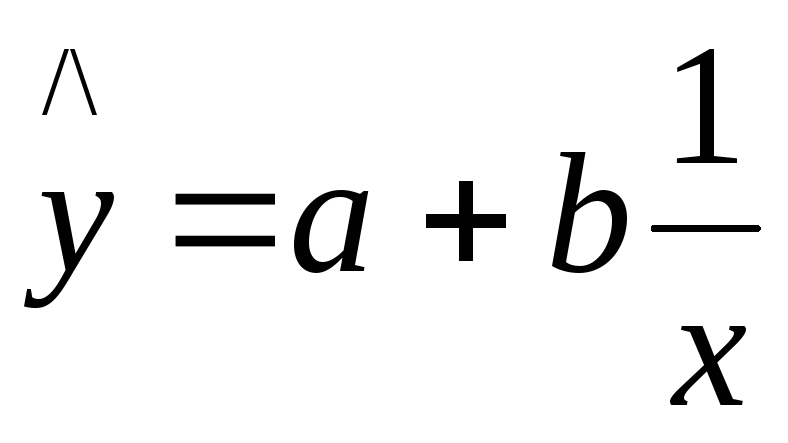, заменяя переменную, получим линейное уравнение регрессии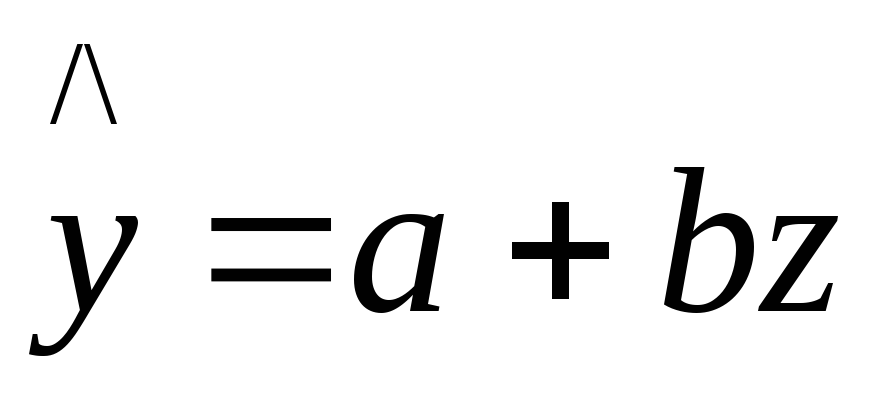, оценка параметров которого может быть произведена по методу наименьших квадратов.

Уравнение логарифмической функции

(3.1.4)

линейно по параметрам. Оценку параметров уравнения логарифмической функции (3.1.17) можно проводить с помощью метода наименьших квадратов, используя систему уравнений Гаусса:

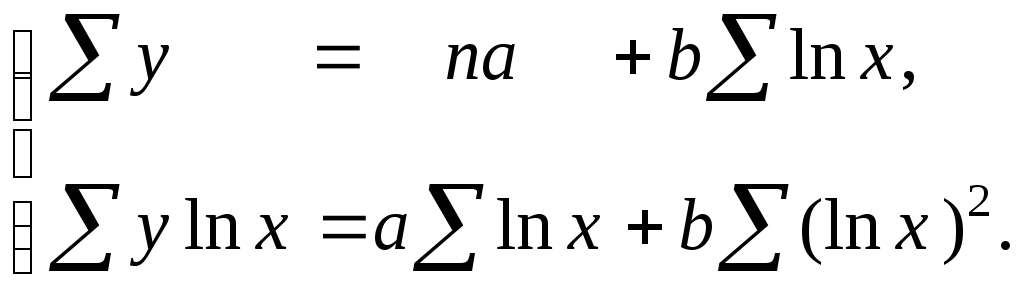(3.1.5)

Модель степенной регрессии

(3.1.6)

нелинейная относительно оцениваемых параметров. Однако, логарифмирование уравнения (3.1.6), приводит его к линейному виду . Оценку параметров этого уравнения можно проводить с помощью метода наименьших квадратов, используя систему уравнений Гаусса:

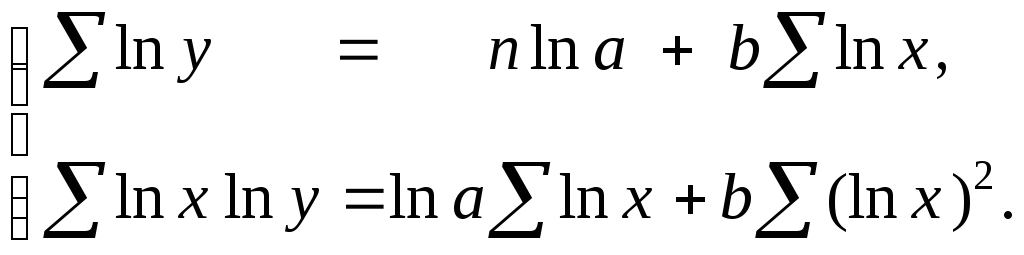(3.1.7)