Методичка к лабораторным / Lab_3_01_new_Tech

Лабораторная работа № 1.

Определение оптических характеристик собирающей линзы.

Погарский М.А.

Цель работы.

В работе определяют фокусное расстояние и радиус кривизны поверхностей двояковыпуклой собирающей линзы. Расчеты и измерения в работе проводятся в предположении, что линза тонкая и все измерения в работе отсчитываются от плоскости линзы.

Задачи

Фокусное расстояние собирающей линзы определяют, измеряя два положения линзы относительно экрана, когда изображение источника оказывается сфокусированным в точку при фиксированном расстоянии между источником и экраном. Радиус кривизны поверхностей линзы рассчитывают по измеренному фокусному расстоянию линзы и заданному значению относительного показателя вещества линзы.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ЛУЧЕВОЙ (ГЕОМЕТРИЧЕСКОЙ) ОПТИКИ

1. Введение

скую систему, т. е. через совокупность различныхftсред, ограниченных теми или иными поверхностями и диафрагмами. Однако в очень многих областях, имеющих важное

Явления интерференции и дифракции света показывают, что распространение света

представляет собой волновой процесс. С помощью волновой теории мы можем решать

техника) и в вопросах об образованииraизображения (оптотехника), решение можно получить гораздо более простым путем, с помощью представлений геометрической оптики.

задачи о распространении света как в однородной среде, так и через любую оптиче-

практическое значение, в частности, в вопросе о формировании светового пучка (свето- D

Геометрическая оптика оперирует понятием отдельных световых лучей, подчиняющихся известным законам преломления и отражения и независимых друг от друга: 1. Закон прямолинейного распространения света.

2. Закон независимости световых пучков.

3. Закон отражения света от зеркальной поверхности.

4. Закон преломления света на границе двух прозрачных сред.

Понятие светового луча можно получить из рассмотрения реального светового пучка в однородной среде, из которого при помощи одной или последовательности диафрагм с отверстиями выделяется узкий параллельный пучок. Чем меньше диаметр этих отверстий, тем уже выделяемый пучок, и в пределе, переходя, к отверстиям сколь угодно малым, можно казалось бы получить световой луч как прямую линию. Мы знаем, однако, что подобный процесс выделения сколь угодно узкого пучка (луча) невозможен вследствие явления дифракции. Неизбежное угловое расширение реального светового пучка, пропущенного через диафрагму диаметра D, определяется углом дифракции

φ ~ λ/D. Только в предельном случае, когда λ = 0, подобное расширение не имело бы места, и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление распространения световой энергии. Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и геометрическая оптика есть лишь предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны.

Для обширного круга важных задач светотехники и оптотехники мы имеем возможность пользоваться геометрической оптикой лучей. Однако при пользовании зако-

1

© Кафедра экспериментальной физики СПбГПУ, 2006

нами лучевой оптики нельзя забывать, что они — лишь первое приближение к действительности и что без дифракционных явлений не обходится ни один случай распространения света. Необходимо, следовательно, понимать волновой (дифракционный) смысл этих лучевых (геометрических) построений. Отсюда ясно, что законы лучевой оптики имеют ограниченное применение, и надо уметь ориентироваться, при каких условиях применение этих законов допустимо и будет практически находиться в соответствии с опытом. Оказывается, однако, что даже в практической оптике наиболее тонкие вопросы (например, вопрос о разрешающей силе оптических инструментов) решаются при помощи теории дифракции.

Рассмотрим, как с помощью представлении, используемых в волновой оптике можно объяснить закон преломления. Одним из наиболее важных принципов волновой оптики является принцип Гюйгенса.

Принцип Гюйгенса можно сформулировать следующим образом:

Каждая точка, до которой доходит световое возбуждение, является в свою очередь центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распро-

страняющейся волны.

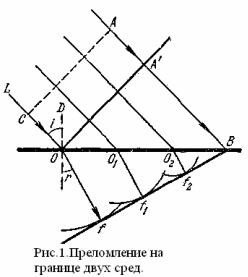
Проанализируем для примера преломление плоской волны на границе двух сред, причем скорость волны в первой среде обозначим через v1, во второй — через v2.

к поверхности преломляющей среды. Пусть в момент t = 0 точка C фронта волны достигла преломляющей среды и совпала с точкой O; тогда за

Пусть i (рис. 1) — угол между CO, перпендикуляромftк фронту волны, и OD, перпендикуляром

rвремя т, потребное для того, чтобы точка A' фрон-

таaволны достигла (в точке B) второй среды, из точки O, как из центра, вторичная волна распространяется на некоторое расстояние Of. Вторич-

Dные волны, имеющие центрами точки Ol O2 и т. д., распространяются к указанному моменту на

соответствующие расстояния, давая во второй среде элементарные сферические волны f1, f2, ... По принципу Гюйгенса действительное положение волнового фронта указывается огибающей элементарных волн, т. е. плоскостью Bf2f1f. Очевидно, что

подставляя сюда значения A'B = v1τ и Of = v2τ, получим:

v1τsin r — v2τsin i,

или

sin i/sin r = vl/v2 = n.

Мы видим, что теория Гюйгенса дает объяснение закона преломления, причем оказалось, что значение показателя преломления легко привести в согласие с результатами опыта Фуко, произведенного более полутораста лет спустя.

Так же естественно объясняется с точки зрения принципа Гюйгенса закон отражения волн.

2. Основные определения. Принцип взаимности

Пользуясь представлениями лучевой оптики, мы рассматриваем каждую светящуюся точку источника как вершину расходящегося пучка лучей, именуемого гомоцентри- ческим, т. е. имеющим общий центр. Если после отражения и преломления этот пучок превращается в пучок, сходящийся также в одну точку, то и последний представляет собой гомоцентрический пучок и центр его является изображением светящейся точки.

2

© Кафедра экспериментальной физики СПбГПУ, 2006

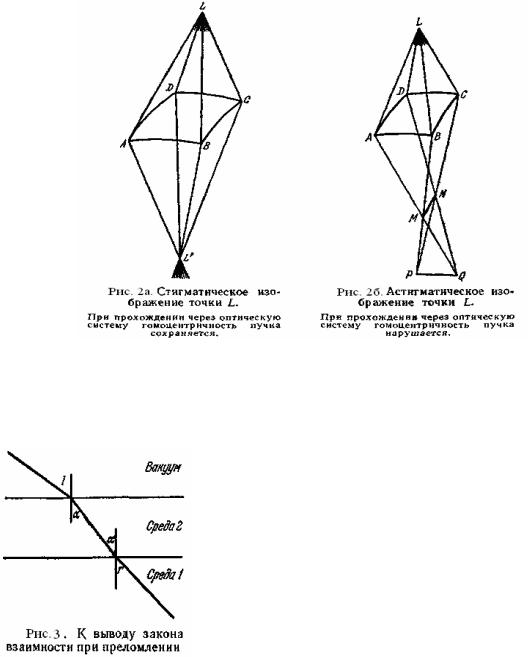
При сохранении гомоцентричности каждая точка источника дает одну точку изображения.

Такие изображения называются точечными или стигматическими (рис. 2.а). В силу обратимости (взаимности) световых лучей (см. ниже) изображение можно рассматривать как источник, а источник — как изображение. Поэтому при стигматическом изображении центры наших пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся. Соответственные лучи и пучки также называются сопряженными. Поверхность, нормальная к лучам, называется волновой поверхностью. Волновая поверхность гомоцентрического пучка в однородной и изотропной среде есть, очевидно, сферическая поверхность.

Если в результате отражения и преломления пучок перестает быть гомоцентрическим, то волновая поверхность перестает быть сферой. Стигматичность изображения теряется, и точка уже не изображается точкой (рис. 2.б). Так как в практической оптике обычно ставится задача получения изображений, точно передающих форму источника, то важнейшим вопросом лучевой оптики является выяснение условий сохранения гомоцентричности пучков.

В основе всех построений лучевой оптики лежат законы преломления и отражения света. Мы рассмотрели содержание и показали, какой смысл вкладывает в них волновая теория. Здесь мы воспроизведем лишь математическую формулировку этих законов, придав ей такое выражение, которое позволяет рассматривать вопросы преломления и отражения совместно, так что из формул, касающихся преломляющих систем (линз),

могут быть сразу получены заключения и для отражающих систем (зеркал).

Однако предварительно покажем, что при явлениях преломления и отражения соблюдается закон взаимности, или обратимости световых лучей.

Пусть среда 1 отделена от вакуума тонкой плоскопараллельной пластинкой среды 2 (рис. 3); n1 n2 и N21 — абсолютные и относительный показатели преломления соответствующих сред. Из рис. 3 ясно, что

Отсюда

3

© Кафедра экспериментальной физики СПбГПУ, 2006

Последняя формула справедлива при любой толщине среды 2.

Перейдем к предельному случаю, когда среда 2 становится исчезающе тонкой, т. е. к случаю непосредственного преломления из вакуума в среду 1. Тогда имеем

sin i/sin r = n1. Сопоставляя эти две формулы, найдем N21 = n1/n2. Повторяя те же рассуждения для случая, когда тонкий слой среды 1 отделяет среду 2 от вакуума, найдем N12 = n2/n1 или N12 = n2/n1, т. е. показатель преломления первой среды относительно второй (N12) равен обратному значению показателя преломления второй среды относи-

тельно первой (N21).

Отсюда непосредственно следует, что при преломлении на границе двух сред лучи остаются взаимными, т. е. при изменении направления лучей на обратное их взаимное расположение не меняется (рис. 4а). В законе отражения этот принцип обратимости светового пути также действителен, как легко видеть из рис.4б без дальнейших объяснений.

Его можно получить из предыдущей формулы, положив n1 = - n2, откуда sin i = — sin r, i = — r.

Итак, закон отражения получается из закона преломления, если положить n2 = - n1 и под r подразумевать угол отражения. Таким образом, любую формулу, выведенную для преломляющих систем, можно использовать для описания явлений в отражающих системах.

3. Преломление (и отражение) на сферической поверхности

Предположим, что две среды с показателями преломления n1 и n2 разделяются сферической поверхностью ρ (рис. 5). На линии LL', проходящей через центр нашей сферы O, поместим точечный источник света L. Рассмотрим узкий гомоцентрический конус лучей, падающий из L на поверхность раздела двух сред.

Мы предполагаем пучок настолько узким, т.е. угол ψ настолько малым, что прак-

тически можно считать отрезок LS равным LA, L'S равным L'A и т. д. Такой узкий пучок

1 Знак минус означает, что углы i' и i отсчитываются в разные стороны от нормали к поверхности.

4

© Кафедра экспериментальной физики СПбГПУ, 2006

будем называть параксиальным. Итак, условие параксиальности пучка есть

LS ~ LA и L'S ~ L'A.

Возьмем какой-либо луч из этого пучка, например LA, падающий на ρ под углом i, построим сопряженный ему преломленный луч AL' (угол преломления r) и найдем положение точки, в которой преломленный луч пересечет ось системы.

Из треугольника ALO имеем

Соотношение (3) позволяет найтиrдлину a2 = SL', если задано a1 — LS, т. е. позволяет отыскать положение точки L' по заданному L. При выводе его мы, кроме закона преломления, пользовались еще допущением, что луч LA принадлежит к параксиальному

пучку. Следовательно, соотношение справедливо для любого луча параксиального пучка. Из формулы (3) видно, что a2 при заданных параметрах задачи (n1, n2, R) зависит только от a1. Таким образом, все лучи параксиального гомоцентрического пучка, выходящего из L, пересекают ось в одной и той же точке L', которая является, следовательно, стигматическим изображением источника L. Итак, гомоцентрический пучок при преломлении на сферической поверхности остается гомоцентрическим, если он удовлетворяет условию параксиальности. Основное уравнение (3) охватывает все случаи преломления лучей на сферической поверхности. Пользуясь установленным выше правилом знаков, мы можем разобрать случай выпуклой (R > 0) или вогнутой (R < 0) поверхности.

Точно так же в зависимости от того, будут ли a1 и a2 иметь разные знаки или одинаковые, мы будем иметь случаи, когда изображение располагается с противоположной по сравнению с источником стороны преломляющей поверхности или лежит по одну сторону с ним. В первом случае (a2 > 0) точка, именуемая изображением, есть действительно точка пересечения преломленных лучей. Такое изображение называется действительным. Во втором случае (a2 < 0), очевидно, преломленные лучи, идущие во второй среде, остаются расходящимися и реально не пересекаются. В этом случае название изображения относится к той воображаемой точке, которая представляет собой место пересечения предполагаемого продолжения преломленных лучей. Такое изображение называется мнимым. Наши рассуждения и формула (3) показывают, что гомоцентриче-

5

© Кафедра экспериментальной физики СПбГПУ, 2006

ский пучок после преломления направлен так, что его лучи или пересекаются в одной точке (действительное изображение), или могут быть представлены как пересекающиеся в одной точке (мнимое изображение). Именно в этом смысле он и остается гомоцентрическим. Так как для всех наших рассуждений нам важно знать направление световых лучей, то при всех построениях мы одинаково можем пользоваться как действительным, так и мнимым изображением.

Формула (3) показывает также, что если бы источник был в L', то изображение расположилось бы в L (взаимность).

4. Центрированная оптическая система

Случай преломления на одной сферической поверхности сравнительно редок. Большинство реальных преломляющих систем содержит по крайней мере две преломляющие поверхности (линза) или большее их число.

Следовательно, соотношение (3) можно последовательно применить к каждой преломляющей поверхности сложной оптической системы, понимая под L изображение точечного источника, образованноеDвсеми предыдущими поверхностями. Очевидно, что при этом ах может быть и положительным, если на рассматриваемую поверхность падает сходящийся пучок лучей (см. рис. 6, поверхность ρ3).

Для точки L1 лежащей на оси, пучок параксиальных лучей сохраняет гомоцентричность, т. е. он соберется в точке L2, из которой также пойдет параксиально и, следовательно, сохранит гомоцентричность, и т. д.

Итак, гомоцентрический параксиальный пучок остается гомоцентрическим при произвольном числе преломлений (и отражений) в центрированной сферической системе; таким образом, точка L1 дает в центрированной системе стигматическое изображение (действительное или мнимое).

Подобным же образом, можно показать, что небольшой участок плоскости, расположенный в первой среде перпендикулярно к оптической оси центрированной системы, изобразится в последней преломляющей среде сопряженной плоскостью, также перпендикулярной к оптической оси, причем изображение остается геометрически подобным объекту. Наличие двух фокусов и двух фокальных поверхностей, установленное для одной сферической поверхности, сохраняется также и для всякой центрированной системы поверхностей.

Для центрированной системы сохраняет смысл и понятие главных плоскостей как таких сопряженных плоскостей, в которых объект и изображение имеют одинаковые величину и направление. Но в то время как для одной преломляющей сферической поверхности обе главные плоскости сливались в одну, касающуюся сферической поверхности в ее вершине S, для центрированных поверхностей эти две плоскости, вообще говоря, не совпадают. Фокусные расстояния системы, так же как и в случае одной сферической поверхности, есть расстояния от соответствующей главной плоскости до фокуса.

6

© Кафедра экспериментальной физики СПбГПУ, 2006

5. Преломление в линзе. Общая формула линзы

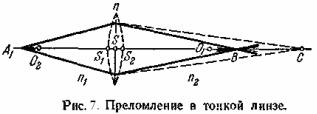
Большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал (обычно стекло) от окружающего воздуха. Такая система представляет, очевидно, обычную линзу.

Линза называется тонкой, если обе ее вершины можно считать совпадающими, т. е. если толщина линзы b мала по сравнению с R1, и R2, радиусами кривизны ограничивающих поверхностей. На рис. 7 для ясности линза изображена толстой. В дальнейших расчетах будем полагать, что точки S1 и S2 сливаются, и обозначим их буквой S. Все расстояния будем отсчитывать от этой точки S, которая практически совпадает с S1 и S2. Точка S носит название оптического центра линзы. Любой параксиальный луч, проходящий через S, практически не испытывает преломления. Действительно, для таких лучей участки обеих поверхностей линзы можно считать параллельными, так что луч, проходя через них, не меняет направления, но лишь смещается параллельно самому себе (преломление в плоскопараллельной пластинке), а так как толщиной линзы мы пренебрегаем, то смещение это ничтожно и луч практически проходит без преломления. Луч, проходящий через оптический центр, мы назовем осью линзы. Та из осей, которая проходит через центры обеих поверхностей, называется главной, остальные — побочными.

Складывая второе уравнение с первым, получим:

Эта общая формула линзы годна для линз выпуклых и вогнутых при любом расположении источника и соответствующем расположении фокуса. Нужно только принять во внимание знаки a1, a2, R1, R2, считая их положительными, если они отложены вправо от линзы, и отрицательными, если они отложены влево от линзы (как было сделано при выводе формулы (2). Если знаки a1 и a2 одинаковы, то одна из сопряженных точек — мнимая, т. е. в ней пересекаются не сами лучи, а их воображаемые продолжения.

7

© Кафедра экспериментальной физики СПбГПУ, 2006

риал тонкой линзы преломляет меньше, чем окружающая среда (например, воздушная полость в воде), то линзы вида рис. 9, а будут рассеивающими, а вида рис. 9, б — собирающими.

Вводя фокусное расстояние линзы, придадим

где D — оптическая сила линзы, измеряемая в диоптриях — дпт.

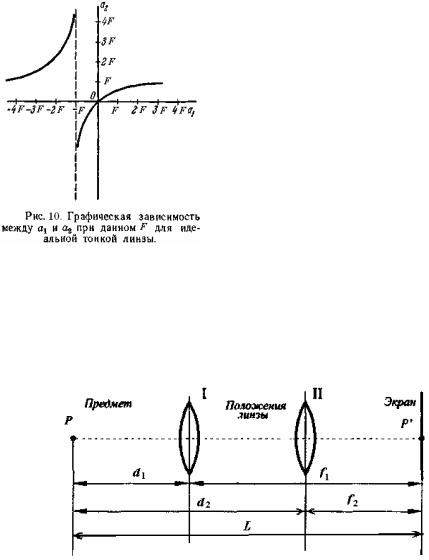
Зависимость между a1 и a2 графически изображена на рис. 10. Легко видеть, что изменение величины a1 приводит к изменению a2 того же знака.

Другими словами, изображение сдвигается вдоль оси в том же направлении, что и объект. Исключение составляет лишь точка a1 = - F1, при прохождении которой изображение переходит из a2 = + ∞ в a2 = - ∞.

При заданном положении экрана и предмета (источника света) существует два по-

Используя формулу (7) для двояковыпуклой линзы для двух положений её, когда изображение сфокусировано, при фиксированном расстоянии между предметом и экраном L > 4F, получим систему уравнений:

9

© Кафедра экспериментальной физики СПбГПУ, 2006

Установка.

Схема опыта дана на рис.

Здесь: 1 — источник; 2 — двояковыпуклая симметричная линза из стекла с относительным показателем преломления n = 1,6; 3 — экран.

Измерения.

Соберите схему согласно рисунка. При фиксированном расстоянии между источником и экраном L1 измерьте два положения линзы относительно экрана f1 и f2, когда луч света сфокусируется в точку на экране. Запишите полученные измерения в таблицу.

ного расстояния линзы и погрешность измерения.

Контрольные вопросы.

1.Какой пучок лучей называется гомоцентрическим?

2.Какие изображения называются стигматическими?

3.Каково основное правило для построения хода лучей через тонкую линзу?

4.Почему при заданном положении экрана и предмета (источника света) существует два положения линзы, при которых получается резкое изображение, если только расстояние между предметом и экраном L > 4F? Доказать, используя формулу для тонкой линзы.

Литература.

1.Савельев И.В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика.— М.: Наука, 1988.

2.Лансберг Г.С. Оптика.—М.: Наука, 1976.

10

© Кафедра экспериментальной физики СПбГПУ, 2006