Основные определения теории графов (включая ориентированные графы).

11. Основные определения теории графов (включая ориентированные графы).

Граф описывается перечислением множества вершин и рёбер. Объекты представляются как вершины графа, а связи — как рёбра.

Граф называется связным, если для любых вершин u,v есть путь из u в v.

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Х = {х_i}, i = 1, 2, 3, 4 – множество вершин; А = {a_i }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i,

Ориентированный граф (кратко орграф) — граф, вершины которого соединены направленными ребрами.

Маршрутом в орграфе называют чередующуюся последовательность вершин и рёбер, вида v₀{v₀,v₁}v₁{v₁,v₂}v₂...v_n (вершины могут повторяться). Длина маршрута — количество рёбер в нем.

Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой. Контур если замкнутый путь.

Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

Орграфы широко применяются в программировании как способ описания систем со сложными связями.

Способы матричного представления графов, их сравнение.

12. Способы матричного представления графов, их сравнение.

Граф описывается перечислением множества вершин и дуг. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Х = {х_i}, i = 1, 2, 3, 4 – множество вершин; А = {a_i }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i,

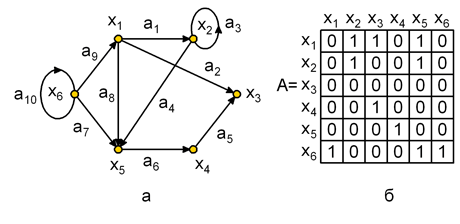
Матричное представление графов

Графы удобно представлять в виде матриц смежности.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа ), однозначно представляющая его структуру.

A = {a_ij}, i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, если дуга (х_i, х_j),

a_ij = 0, если нет дуги (х_i, х_j).

Г(х₂) = { х₂, х₅}.

Сравнение матриц графов.

Матрицы графов сравниваются для того чтобы выявить визуально незаметное сходство структуры графов.

Для сравнения графов используют их матричное представление. Из одной матрицы вычитается другая. Чем меньше полученный результат, тем более похожи графы.