3.1. Нарахування складних річних відсотків

Формула нарощування. В середнє- і довгострокових фінансово-кредитних операціях, якщо відсотки не виплачуються одразу після їх нарахування, а приєднуються до суми боргу, застосовують складні відсотки. База для нарахування складних відсотків на відміну від простих не залишається постійною — вона збільшується з кожним кроком в часі. Абсолютна сума відсотків, що нараховуються, зростає, і процес збільшення суми боргу відбувається з прискоренням. Нарощування по складних відсотках можна представити як послідовне реінвестування засобів, вкладених під прості відсотки на один період нарахування. Приєднаннянарахованих відсотків до суми, яка послужила базою для їх нарахування, часто називають капіталізацією відсотків.

Знайдемо формулу для розрахунку нарощеної суми за умови, що відсотки нараховуються і капіталізуються один раз в році (річні відсотки). Для цього застосовується складна ставканарощування. Для запису формули нарощування застосуємо ті ж позначення, що і у формулі нарощування по простих відсотках:

Р — первинний розмір боргу (позики, кредиту, капіталу і т.д.)

S — нарощена сума на кінець терміну позики

п — термін, число років нарощування

i — рівень річної ставки відсотків, представлений десятковимдробом.

Очевидно, що в кінці першого року відсотки рівні величині Pi, а нарощена сума складе Р + Pi= Р(1+i). До кінця другого року вона досягне величини

Р(1+i)+Р(1+i)i=P(1+i)² і т.д. В кінці n-го року нарощена сума буде дорівнювати

S = P(l + i)ⁿ (3.1)

Відсотки за цей же термін в цілому такі:

I= S - Р= Р[(1+ i)ⁿ- 1] (3.2).

Частина з них отримана за рахунок нарахування відсотків на відсотки. Вона складає

I_р = Р[(1 + i)ⁿ - 1] - Pni = Р [(1 + i)ⁿ – (1 + ni)] (3.3)

Очевидно, що із збільшенням терміну частка відсотків на відсотки в загальній сумі нарахованих відсотків збільшується.

Як показано вище, зростання по складних відсотках є процесом, відповідним геометричній прогресії, перший член якої рівний Р, а знаменник — (1 + i). Останній член прогресії рівний нарощеній сумі в кінці терміну позики.

Величину (1 + i)ⁿ називають множником нарощування по складних відсотках. ПРИКЛАД 3.1. Якої величини досягне борг, рівний 1 млн грн. через 5 років при зростанні по складній ставці 15,5% річних? По формулі (3.1) знаходимо

S = 1000000(1 + 0.155)⁵ = 2055464,22 грн.

Причому із загальної суми нарахованих відсотків, 280464,22 грн. доводиться на відсотки на відсотки. Час при нарощуванні по складній ставці звичайно вимірюється як ACT/ ACT.

Як бачимо, величина множника нарощування залежить від двох параметрів — i і п. Слід зазначити, що при великому терміні нарощування навіть невелика зміна ставки помітно впливає на величину множника. У свою чергу дуже великий термін приводить до страхітливих результатів навіть при невеликій процентній ставці. Тут доречна наступна ілюстрація. Острів Манхеттен, на якому розташована центральна частина Нью-Йорка, був куплений (а точніше виміняний) за 24 долл.Вартість землі цього острова через 350 років оцінювалася приблизно в 40 млрд долл., тобто первинна сума збільшилася в 1,667 х 109разів! Таке зростання досягається при складній ставці, рівній всього 6,3 % річних.

Очевидно, що дуже висока (інфляційна) процентна ставка може бути застосована тільки для короткого терміну. Наприклад, вже при i = 120% (а така інфляційна ставка не так вже давно спостерігалася в Росії, правда для короткострокових позик) і п = 10 маємо жахливий за розміром множник нарощування (1 + 1,2)10 = 2656.

Формула нарощування по складних відсотках (3.1) отримана для річної процентної ставки і терміну, що виміряється в роках. Проте її можна застосовувати і при інших періодах нарахування. В цих випадках i означає ставку за один період нарахування (місяць, квартал і т.д.), а n — число таких періодів. Наприклад, якщо i — ставка за півріччя, то п — число півріч і т.д.

Формули (3.1)—(3.3) припускають, що відсотки на відсотки нараховуються по тій же ставці, що і при нарахуванні на основну суму боргу. Ускладнимо умови нарахувань відсотків. Нехай відсотки на основний борг нараховуються по ставці i, а відсотки на відсотки — по ставці r≠ i В цьому випадку

S = Р + Pi[1+ (1 + r) + (1 + r)² +...+ (1 + r)^n-1].

Ряд в квадратних дужках є геометричною прогресією з першим членом, рівним 1, і знаменником (1 + r). У результаті маємо

(3.4)

Нарахування відсотків в суміжних календарних періодах. Вище при нарахуванні відсотків не бралося до увагирозташування терміну нарахування відсотків щодо календарних періодів. Разом з тим, часто дати початку і закінчення позики знаходяться в двох періодах. Ясно, що нараховані за весь термін відсотки не можуть бути віднесені тільки до останнього періоду. В бухгалтерському обліку, при оподаткуванні, нарешті, в аналізі фінансової діяльності підприємства виникає задача розподілу нарахованих відсотків по періодах.

Загальний термін позики ділиться на два періоди n₁ і п₂. Відповідно

I=I₁+I₂ (3.5)

де I₁=Р[(1+ i)ⁿ₁ - 1],

I₂= Р(1+ i)ⁿ₁[(1+i)ⁿ₂ - 1]=Р[(1+ i)ⁿ – (1+ i)ⁿ₁ ].

ПРИКЛАД 3.2. Позика була видана на два роки — з 1 травня 2005 р. по 1 травня 2007 р. Розмір позики 10 млн грн. Необхідно розподілити нараховані відсотки (ставка 14% ACT/ACT) по календарних роках. Отримаємо наступні суми відсотків (в тис.грн.):

за період з 1 травня до кінця року (244 дні): 10000(1,14^244/365 - 1) =

= 915,4;

за 2006 г.: 10000 х 1,14^244/365 х 0,14 = 1528,2;

с 1 січня до 1 травня 2007 г. (121 день): 10 000 х 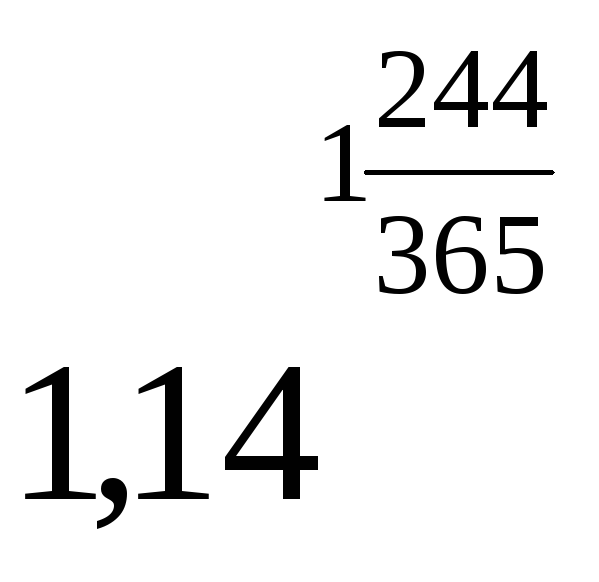х (1,14^121/365 - 1) = 552,4.

Разом за весь термін — 2996 тис. грн. Такий же результат отримаємо для всього терміну в цілому:

10000 х(1,14² - 1) = 2996.

Змінні ставки. Якщо використовуються змінні в часі ставки, то нарощування відбувається по формулі

S = P(l + i₁)ⁿ₁(l + i₂)ⁿ₂ ...(l + i_k)ⁿ_k (3.6)

де i₁, i₂,..., i_k — послідовні значення ставок; n₁, n₂,..., п_к — періоди, протягом яких "працюють" відповідні ставки.

ПРИКЛАД 3.3. Термін позики — 5 років, договірна базова процентна ставка — 12% річних плюс маржа 0,5% в перші два роки і 0,75% в роки, що залишилися. Множник нарощування в цьому випадку складе

q = (1 + 0,125)²(1 + 0.1275)³ = 1,81407.

Нарахування відсотків при дробовому числі років. Часто термін в роках для нарахування відсотків не є цілим числом. В правилах ряду комерційних банків для деяких операцій відсотки нараховуються тільки за ціле число років або інших періодів нарахування. Дробова частина періоду відкидається. В більшості ж випадків враховується повний термін. При цьому застосовують два методи. Згідно першому, назвемо його загальним, розрахунок ведеться безпосередньо по формулі

S = P(l + i)ⁿ. (3.7).

Другий, змішаний, метод припускає нарахування відсотків за ціле число років по формулі складних відсотків і за дробову частину терміну по формулі простих відсотків:

, (3.8)

Де n=a+b– термін позики, а –ціле число років, b – дробова частина року.

ПРИКЛАД 3.4. Кредит у розмірі 3 млн грн. виданий на 3 роки і 160 днів (n = = 3,43836 роки) під 16,5% складних річних.

Суму боргу на кінець терміну визначимо по формулі (3.1):

S = 3000000 х 1,165^3'43836 = 5071935,98 грн., у свою чергу, змішаний метод дає S = 3000000 х 1,165³ х (1 + 0,43836 х 0,165) = 5086595,98 грн.