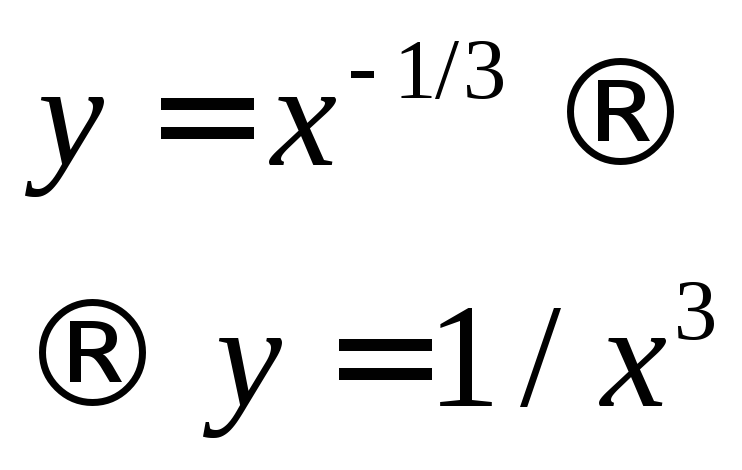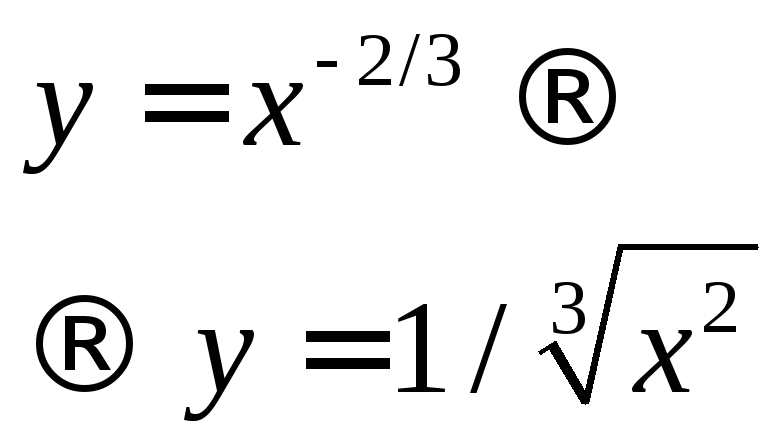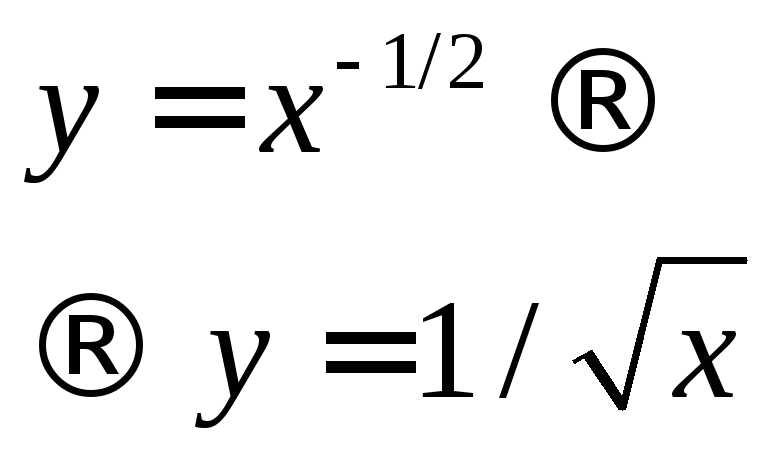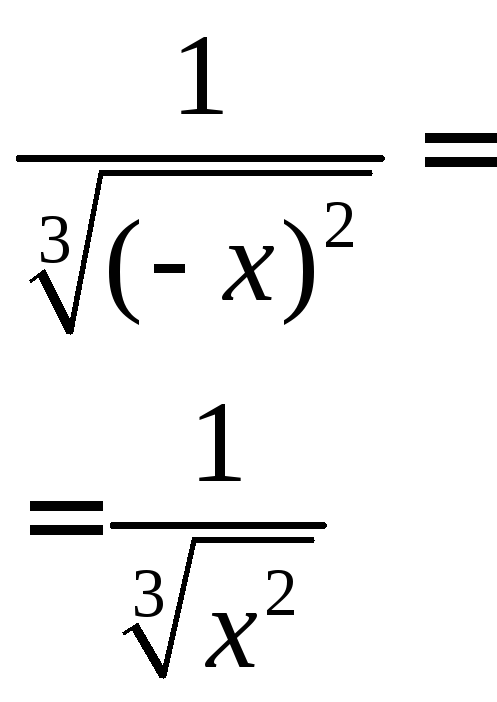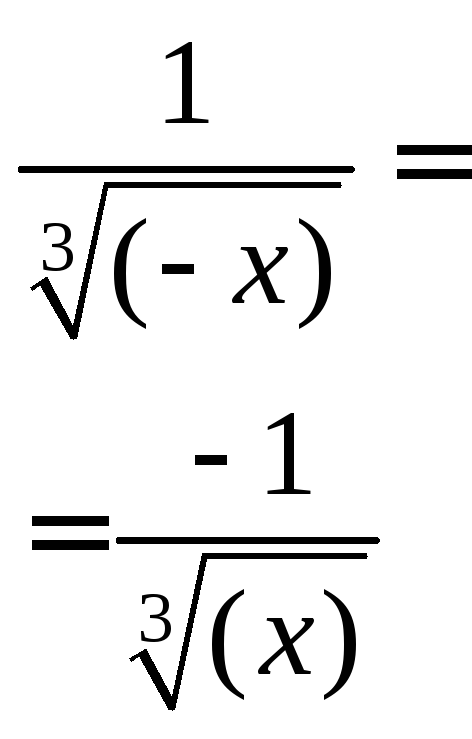12 Основні елементарні функції, їхні властивості та графіки

Визначення функції

Якщо кожному елементу х, що належить множині із деяких елементів Х, ставиться у відповідність один і тільки один елемент у із множини інших елементів Y, то на множині Х задана функція f(x).

У випадку числових множин Х, Y маємо числову функцію f(x).

Визначення та способи задання числової функції

Означення. Функцією y=f(x) називається така відповідність між множинами D i E дійсних чисел R, за якої кожному значенню змінної хDR відповідає одне й тільки одне значення змінної yER. При цьому:

х – незалежна змінна, або аргумент;

у – залежна змінна, або функція;

f – символ закону відповідності;

D – область визначення функції;

Е – множина значень функції.

Зауваження 3. Поряд з позначенням функції y=f(x) вживається також і позначення y=y(x), тобто символом функції слугує позначення змінної y.

Розрізняють такі способи задання функції: алгоритмічний (відповідність між множинами D i E описують словами), аналітичний (відповідність між множинами D i E задають формулою – аналітичним виразом), графічний і табличний.

Числову функцію у(х) можна задати аналітичним способом , тобто у вигляді формули

у= f(х),

де символ f в загальній формі позначає арифметичні, алгебраїчні та інші операції, які потрібно здійснити над конкретним значенням незалежної змінної х, щоб отримати відповідне значення залежної змінної у. Наприклад, у=3х²+4.

Графіком функції y=f(x) є сукупність точок М(х,у) на координатній площині ОХY, координати (х,у) кожної з яких пов’язані формулою

,

тобто – сукупність точок М(х, f(x)) на координатній площині.

Якщо областю визначення функції f(x) є всі точки, що належать відрізку а, b осі ОХ, то графіком функції є деяка лінія або сукупність ліній та окремих точок.

Зокрема, функція у = kх+b, де k, b – має назву лінійної функції, її графіком є пряма лінія, яку можна побудувати, вказавши координати 2-х точок, через які проходить ця пряма.

Серед функцій, що належать до класу основних елементарних функцій виділимо такі:

степенева функція у = х^a , показникова функція у=а^x , логарифмічна функція , тригонометричні функції sin x, cos x, tg x, ctg x.

12.1 Степенева функція у = х^a

Для степеневої функції незалежною змінною х є основа степеня, показник а степеня натомість – постійне число а 0. Області визначення і значень степеневої функції, її властивості та особливості графіка визначаються в залежності від конкретного значення а (див.Табл.2).

12.2 Показникова функція у=а^x

Для показникової функції незалежною змінною є показник степеня, основа степеня а натомість – постійне число (а >0, а 1 ).

Властивості показникової функції у=а^x та її графік (Рис.4)

Область визначення DR , тобто вся числова вісь –  < х < +  .

Оскільки результат піднесення додатного числа а до довільного степеня є додатною величиною, тобто а^x >0 ,то область значень показникової функції E ] 0; +  [ , тобто відкрита піввісь 0 < у < + . Таким чином, графік показникової функції розміщується у верхній півплощині у > 0 і не перетинає вісь ОХ, Рис.4.

Графіки функцій у=а^x з різними значеннями основи степеню а перетинають вісь ОY в одній і тій самій точці (0;1), оскільки а⁰ =1 для а  0.

За зростання х функція у=а^x є у випадку а>1 є монотонно зростаючою (  ), а у випадку 0<а<1 – монотонно спадною ( ), Рис.4.

12.3 Логарифмічна функція y = log_ax

Визначення логарифма

Логарифмом за основи а даного числа b є таке число log_ab (позначення цього числа), до якого потрібно піднести основу а (задане число а >0, а  1 ), щоб отримати число b,тобто

.

Наприклад, , оскільки 3⁴=81; , оскільки 2^-3=(1/2)³ = 1/8;

, оскільки (1/5)^-2 = 5⁺²=25; , оскільки

Зауваження 2. Для десяткового логарифма (за основи а=10) вживається спеціальне скорочене позначення lg b.

Наприклад, lg 1000 = 3, оскільки 10³=1000; lg 0,01 = –2, оскільки 10^–2=0,01.

Основні властивості логарифмів

log_a 1 = 0, оскільки а⁰ = 1;

log_a а = 1, оскільки а¹ = а;

log_a b^с = c log_a b^с ;

,

тобто операції піднесення до степеня та логарифмування при одній і тій самій основі а є взаємно оберненими і тому при послідовному виконанні ця пара операцій „ліквідується^”;

log_a (bc) = log_a b + log_a c ;

log_a (b/c) = log_a b – log_a c ;

log_a b = log_c b / log_c a (Правило приведення логарифма до заданої основи с).

Властивості логарифмічної функції y = log_ax та її графіка (Рис.5)

Для логарифмічної функції y = log_ax незалежною змінною є величина х, основа степеня а – постійне число (а>0, а1).

Область визначення D] 0; +  [ , тобто відкрита піввісь 0 < x < + . Таким чином, графік логарифмічної функції розміщується у правій півплощині х > 0 і не перетинає вісь ОY.

Область значень E R , тобто вся числова вісь –  < у < +  .

За всіх значень основи а логарифма графіки функцій у = log_ax перетинають вісь ОX в одній і тій самій точці (1;0), оскільки log_a 1=0, Рис.5.

За зростання х функція у = log_ax є у випадку а > 0 монотонно зростаючою (  ), у випадку 0 < а < 1 – монотонно спадною ( ), Рис.5.

Порівняння графіків на Рис.4 і на Рис.5, виконаних при однакових лінійних масштабах для координатних осей, показує, що графіки показникової функцій у=а^x та логарифмічної y = log_ax при однаковій основі а симетричні відносно бісектриси 1-го і 2-го квадрантів. Це спільна властивість графіків пар всіх обернених функцій, не лише розглянутої пари.

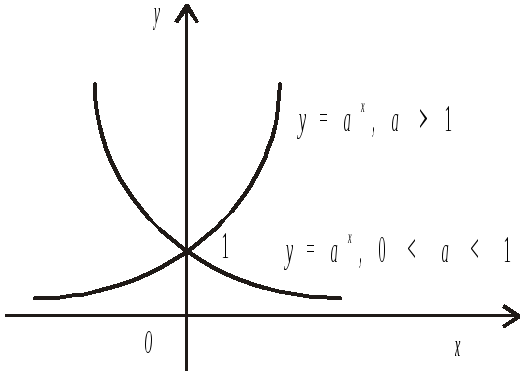
Рис.4

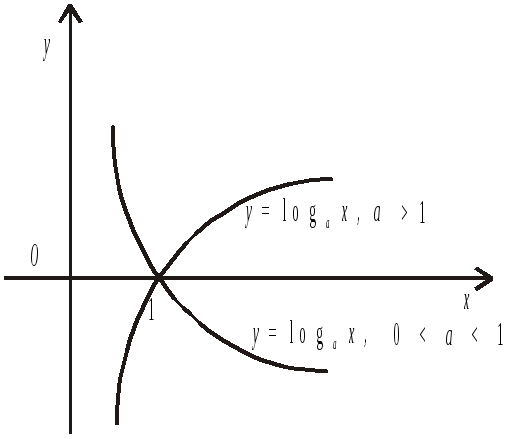
Рис.5

Таблиця 2. Властивості степеневої функції у = х^a за різних значень показника а

Значення показника степеня а	Степенева функція у = хa за конкретного значення а	Область визначення Х	Область значень Y	Функція парна, у(-х) = у(х), графік симетричний відносно осі ОУ	Функція непарна, у(-х) = - у(х), графік симетричний відносно поч. координат	Функція монотонно зростає ( ) чи спадає () з ростом х в усій області визн.
а ціле, додатнє: 1) а непарне 2) а парне	а=3, у = х3 а=2, у = х2	] -  ; +  [ ] -  ; +  [	] -  ; + [ [0; +  [	– (–х)2 = (х)2	(–х)3 = – (х)3 –	 –
а ціле, від’ємне: 3) а непарне 4) а парне	а = -3, у = х-3 у=1/х3 а = -2, у = х-2 у=1/х2	] -  ; 0 [  ] 0; +  [ ] -  ; 0 [  ] 0; +  [	] -  ; 0[  ] 0; +  [ ] 0; +  [	– 1/(–х)2 =1/(х)2	1/(–х)3 = –1/х3 –	 –
а=р/q  Q (а раціональне – простий нескорочуваний дріб, додатний): 5) q, p непарні; 6) q непарне, p парне; 7) q парне, p непарне	q=3, р=1 q=3, р=2 q=2, р=1	] -  ; +  [ ] -  ; +  [ [0; +  [	] -  ; + [ [0; +  [ [0; +  [	– –	– –	 – 
а=р/q  Q (а раціональне – простий нескорочуваний дріб, від’ємний): 8) q, p непарні; 9) q непарне, p парне; 10) q парне, p непарне	q=3, р = -1 q=3, р= - 2 q=2, р=1	] -  ; 0 [  ] 0; +  [ ] -  ; 0 [  ] 0; +  [ ] 0; +  [	] -  ; 0[  ] 0; +  [ ] 0; +  [ ] 0; +  [	– –	– –	 – 
а  R\Q (а іраціонал.): 11) додатне; 12) від’ємне	a =   y=x a=-y=1/x	[ 0; +  [ ] 0; +  [	[0; +  [ ] 0; +  [	– –	– –	 

12.4 Тригонометричні функції у = sin x, у = cos x, у = tg x, у = ctg x

Для функцій значення незалежної змінної – кута x береться (як правило) в радіанах.

Визначення періодичної функції. Функція f(x) називається періодичною, якщо вона задана на всій числовій осі OX і для кожного значення x виконується умова

f(xТ)=f(x),

де число Т = const>0 – період функції.

Оскільки величина nТ, де nN – натуральне число, є також періодом функції, то надалі за період Т функції братимемо мінімальний (основний період).

Якщо відомий графік деякої періодичної функції у = f(x) на проміжку x [а, a+T,] довжина якого дорівнює періоду, то паралельним зсувом її графіка вдовж осі OX вправо на відрізок x[а+T, a+2T] та відповідно – вліво на відрізок x [а–T, a] одержимо графік цієї функції на обох відрізках (див. Рис.8).

Властивості тригонометричних функцій та їхніх графіків

Ці властивості випливають із викладених в Розділі 11понять тригонометричних величин: синуса, косинуса, тангенса і котангенса кута, їхніх властивостей.

Область визначення функцій у= sinx, у=cosx – X R , тобто вся числова вісь – <х<+ .

Область значень функцій у = sinx, у = cosx – Y  [–1; 1], тобто графіки функцій знаходяться в смузі –1 y 1 координатної площини ОХY (див. Рис.6, Рис.7).

Періодом функцій у = sin x, у = cos x є величина T=2, а функцій у=tgx, у=ctg x – величина T= , оскільки згідно з формулами (5), (3) мають місце рівності

sin (  ± 2n) = sin , cos (  ± 2n) = cos , tg (  ± n) = tg , ctg (  ± n) = ctg , n  N.

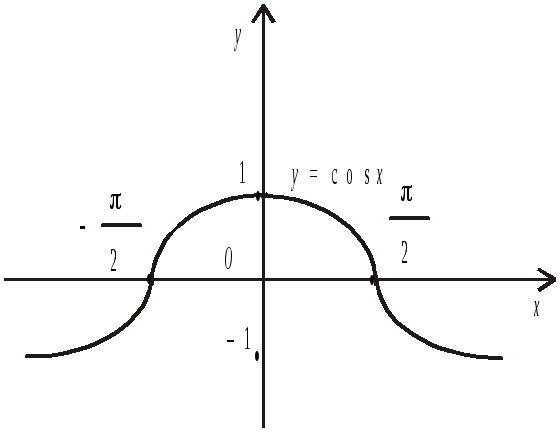Рис.6 Рис.7

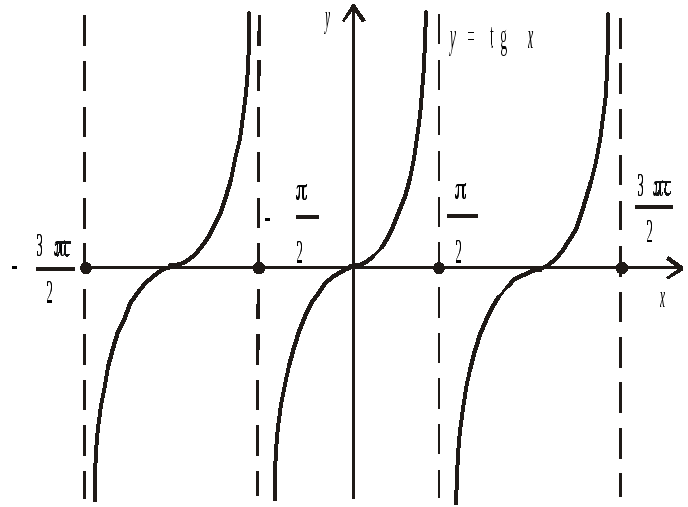Рис.8

Функція у = cos x є парною, тобто cos (–x) = cos (x), отже її графік симетричний відносно осі ОY, Рис.6.

Функції у=sinx, у=tgx, у=ctgx є непарними: sin(–x)=–sin(x), tg(–x)=–tg(x), ctg(–x)=–ctg(x), тобто їхні графіки симетричні відносно початку координат О(0, 0), Рис.7 і Рис.8.

Неважко переконатися в справедливості рівностей

sink =0, sin (/2+k)=(-1)^k;

cos(/2+k )=0, cosk=(-1)^k; k = 1, 2, …

Отже, графік функції у = sinx перетинає вісь ОХ в точках х=k , а графік функції у=cosx – в точках х =/2+k , де k=1,2,…