10

ВЕКТОР-ФУНКЦИИ

Производные вектор-функции одного аргумента :

     Если и дифференцируемы, то:

     Дифференциал вектор-функции

Дифференцирование вектор-функции двух скалярных аргументов

     Если и непрерывны, то = и

ПЛОСКИЕ КРИВЫЕ

     Способы аналитического задания

     1. – векторно-параметрическое уравнение.

     2. – параметрические уравнения.

     3. – явное уравнение.

     4. – неявное уравнение.

Длина дуги кривой

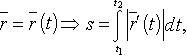
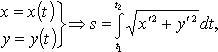
     Дифференциал длины дуги

     В декартовых координатах:

     В полярных координатах:

     Кривизна кривой

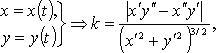
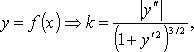
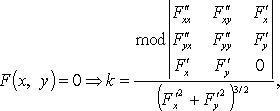
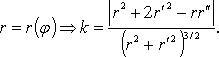
     Радиус кривизны: R = 1/k.

Формулы Френе

где – единичный вектор касательной; – единичный вектор нормали; k – кривизна.

ПРОСТРАНСТВЕННЫЕ КРИВЫЕ

     Способы аналитического задания

     1. – векторно-параметрическое уравнение.

     2. 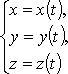– параметрические уравнения.

     3. – явное уравнение.

     4. – неявное уравнение.

     Элементы сопровождающего трехгранника (рис 7.1)

Единичные векторы осей сопровождающего трехгранника

     Касательной

     Главной нормали:

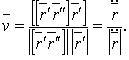
     Бинормали:

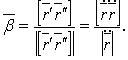
     Длина дуги кривой

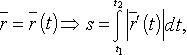
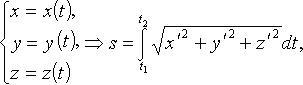
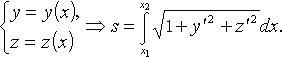
     Дифференциал длины дуги

     В декартовых координатах:

     В цилиндрических координатах:

     В сферических координатах:

Кривизна кривой

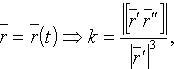
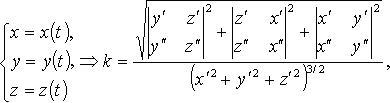
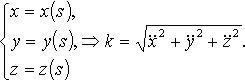
     Радиус кривизны: R = 1/k.

     Кручение  кривой

     

     

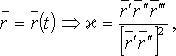
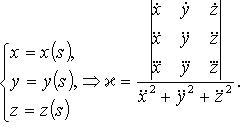
Натуральные уравнения кривой

     Формулы Френе

ПОВЕРХНОСТИ

     Способы аналитического задания

     1. – векторно-параметрическое уравнение.

     2. – параметрические уравнения.

     3. – явное уравнение.

     4. – неявное уравнение.

Единичный вектор нормали поверхности

     

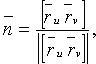
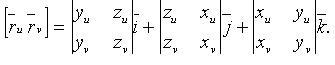
     Первая квадратичная форма поверхности

где

Длина дуги кривой на поверхности

Длина дуги кривой на поверхности может быть вычислена с помощью криволинейного интеграла:

Здесь через I обозначена первая квадратичная форма поверхности (I = ).

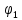Угол между кривыми на поверхности

     Косинус угла между кривыми (или ) и (или ) в точке их пересечения:

     

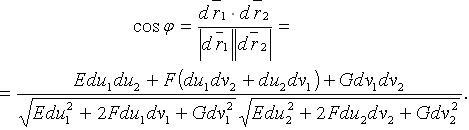
Косинус угла между координатными кривыми:

.

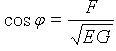     Площадь области на поверхности

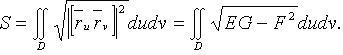
     Вторая основная квадратичная форма поверхности

где – единичный вектор нормали к поверхности;

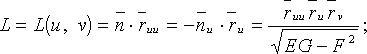
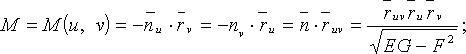
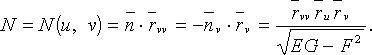
     Нормальная кривизна кривой на поверхности

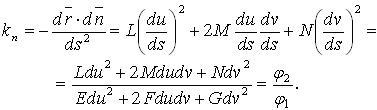
     Главные кривизны

     Главные кривизны поверхности – корни k₁ и k₂ уравнения

Формула Эйлера

где – угол между направлениями, соответствующими нормальным кривизнам k₁ и k₂.

     Средняя (эйлерова) кривизна поверхности

     Полная (гауссова) кривизна поверхности

     Типы точек поверхности

     В эллиптической точке К > 0; в гиперболической точке К < 0; в параболической точке К = 0. 

Источник – сайт «Прикладная математика» Владимирского государственного университета info@pm298.ru.