ФАН / Шпоры / Шпоры / 28-33

28.

Теорема 1. Пространство C[0,1] – банахово.

Пусть x_n(t) – последовательность Коши в C[0,1]. Это значит, что для любого ε>0 существует номер n(ε): (1)

Зафиксируем точку t. Тогда для n>n(ε), m>n(ε) выполняется

Это значит, что числовая последовательность x_n(t) является последовательностью Коши и в силу полноты R сходится.

Получили функцию x₀(t). Осталось доказать, что x₀(t) является непрерывной функцией и последовательность x_n(t) сходится к ней по норме пространства C[0,1], то есть равномерно.

В неравенстве (1) перейдём к пределу при

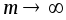
В результате получим, что для n>n(ε) выполняется неравенство

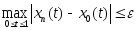
Это как раз и означает, что последовательность x_n(t) сходится к функции x₀(t) равномерно.

Докажем, что x₀(t) непрерывна

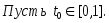
Для ε>0 выберем номер n1 так, чтобы выполнялось

Затем выберем δ>0 так, что из следует

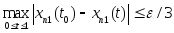
Тогда для любого t из δ-окрестности t₀ имеем:

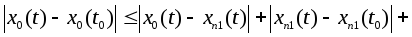
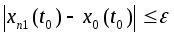
Рассмотрим пространство CL[0,1], которое состоит из непрерывных на отрезке [0,1] функций, однако норма на нем задана с помощью интеграла Лебега:

Утверждение 1. Пространство CL[0,1] – неполно.

Рассмотрим последовательность функций x_n(t):

Данная последовательность является последовательностью Коши.

Действительно, если n>m, то

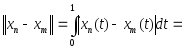
Последовательность x_n(t) сходится в среднем (по норме пространства CL[0,1]) к разрывной функции x₀(t):

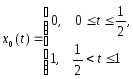
Может ли последовательность x_n(t) сходится по норме пространства CL[0,1] также к другой функции y₀(t), которая является непрерывной?

Если это так, то получаем неравенство:

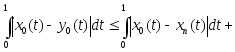
Тогда функция y₀(t) почти всюду равна разрывной функции x₀(t), и значит сама является разрывной

29

31.

32.

33.

Первое доказательство

Пусть отрезок  покрыт бесконечной системой  интервалов. Предположим, что никакое конечное число интервалов из  не покрывает данный отрезок. Разделим отрезок  пополам на два равных отрезка: 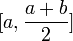 и 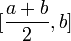. По крайней мере один из них нельзя покрыть конечной подсистемой интервалов из . Обозначим его  и повторим для него процедуру деления пополам.

Продолжая на каждом шаге делить отрезки пополам, мы получим последовательность вложенных отрезков, по длине стремящихся к нулю, такую что каждый отрезок этой последовательности не может быть покрыт конечным числом интервалов из . Но если  — точка, в которую стягиваются отрезки, то, поскольку  лежит на отрезке , она должна входить в некоторый интервал  системы . Тогда все отрезки последовательности , начиная с некоторого номера, будут покрыты интервалом , что противоречит самому выбору этих отрезков. Полученное противоречие доказывает справедливость леммы Гейне — Бореля.