МТФР_EK_дневная / Электронные лекции МТФР / мат теория фин рисков / Глава 1_Риски страхования / 7. Подстроечные коэффициенты

7. Подстроечные коэффициенты.

Пусть темп сбора премий С превышает средние платежи по искам за каждую единицу времени, которые равны . Затем относительная надбавка безопасности равна:

, где - константа.

Пусть - наибольший открытый интервал, для которого существует производящая функция моментов (ПФМ).

Функция распределения .

В случае экспоненциального распределения с параметром константа J=.

- первый начальный момент.

-- общая функция распределения независимых, одинаково распределенных а Х является СВ с функцией распределения Р(х).

S(t) обозначает составной Пуассоновский процесс.

S(t) имеет составное Пуассоновское распределение

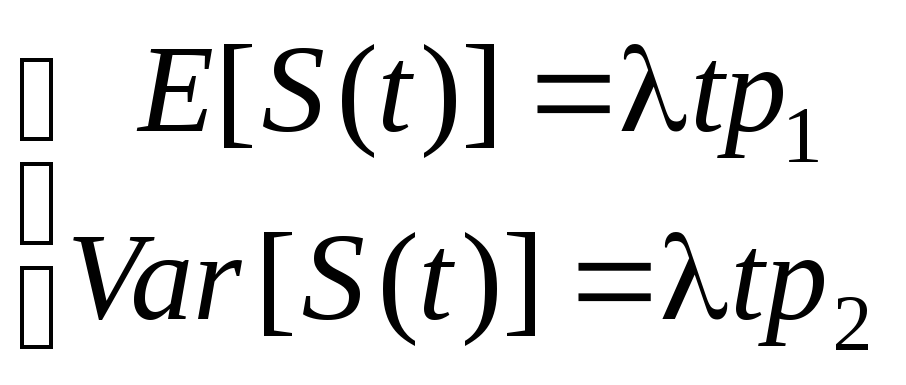
предположим, что при .

Р(х) является непрерывной функцией распределения и имеет ПВ р(х).

Если Р(х) – дискретная функция распределения и имеет ПВ р(х), интегралы заменятся суммами.

Для составного процесса Пуассона рассмотрим равенство:

или эквивалентное выражение, использующее

.

Здесь левая часть представляет собой линейную функцию r, в то время, как правая часть является положительной возрастающей функцией, которая стремится при .

Т.к. вторая производная правой части положительная, то ее график является выпуклым к низу.

Неравенство означает, что наклон левой части превышает наклон правой части в точке r=0.

Из рисунка видно, что уравнение имеет два решения. Кроме тривиального решения r=0 существует положительное решение r=R, которое называется подстроечным коэффициентом.

Теорема:

Для

Д-во:

Знаменатель является значением условной производящей функции отрицательной величины фонда u(T) в точке R при условии, что разорение произойдет, т.е .

Для рассмотрим

(1)

Т.к. , левая часть представляется как

(*)

В первом слагаемом второй части мы можем записать:

Для фиксированного Т не зависит от и имеет составное Пуассоновское распределение с параметром . Отсюда первое слагаемое правой части может быть записано, как

(**)

Выражения (*) и (**) могут быть существенно упрощены, если мы выберем r таким образом, чтобы

Существуют два решения этого уравнения относительно r(смотри рис.).

Берем r=R: при r=R поставим упрощенное равенство в выражение (1), получим

:

Докажем, что (***)

Пусть , . Тогда из (****)

рассмотрим выражение -- оно положительно для достаточно больших t.

Разделим (***) на две части, различая будет ли U(t) меньше или больше, чем значение .

Рассмотрим событие

и дополнение к нему событие :

Тогда

.

Последнее неравенство записано с учетом неравенства Чебышева. При при такой оценке (****).

В общем случае оценка (явная) знаменателем в теореме не представляется возможной.

Однако, т.к. U(t) при является отрицательным обязательно, знаменатель в точке >1 =>

