физика лабараторные / l_r_6

МиНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«тюменский государственный нефтегазовый университет»

ФИЛИАЛ « ТОБОЛЬСКИЙ ИНДУСТРИАЛЬНЫЙ ИНСТИТУТ »

Кафедра электроэнергетики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторной работы №6

«ИЗМЕРЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ БАЛЛИСТИЧЕСКИМ МЕТОДОМ»

по дисциплине: «Физика»

Тобольск 2008 г.

ИНСТРУКЦИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

1. Внимательно изучайте теоретическую часть работы.

2. Приступайте к выполнению работы только после сдачи допуска на проведение лабораторного практикума преподавателю или лаборанту.

3. В случае возникновения неисправности оборудования во время выполнения лабораторной работы немедленно отключить электропитание (отключить питание прибора кнопкой или тумблером «Сеть», либо выдернуть вилку из розетки) или выключить общий выключатель – автомат, о случившемся доложить лаборанту и преподавателю.

4. В случае возникновения вопросов по данной работе обращаться к лаборанту или преподавателю. Строго соблюдать общие инструкции по технике безопасности в лаборатории «Механика и молекулярная физика».

ЛАБОРАТОРНАЯ РАБОТА №6

ИЗМЕРЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ БАЛЛИСТИЧЕСКИМ МЕТОДОМ

ЦЕЛЬ РАБОТЫ: изучение и проверка закона сохранения момента импульса и закона сохранения энергии при неупругом столкновении с помощью баллистического маятника.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В данной работе рассматривается неупругий удар пули о мишень. Абсолютно неупругим называется такой удар, когда столкнувшиеся тела после удара либо движутся с одинаковой скоростью, либо покоятся, при этом кинетическая энергия тел частично или полностью превращается во внутреннюю энергию.

Пусть имеется горизонтальный стержень с двумя одинаковыми грузами m, которые могут перемещаться вдоль стержня и мишенями М (см. рис. 1). Стержень подвешен на стальной проволоке, проходящей через его центр и являющийся осью вращения системы. Пуля, летящая с некоторой скоростью , попадает в мишень М в точке, находящейся от оси вращения на расстоянии l, и застревает в мишени. Удар можно считать абсолютно неупругим, моментом сил пренебречь. Тогда, согласно закону сохранения момента импульса системы пуля – стержень можно написать:

(1)

где m₀ – масса пули; =1,96500г

- ее скорость перед ударом;

l – расстояние от оси вращения до точки удара пули;

– момент инерции грузов с маятником, причем грузы закреплены в определенном положении (момент инерции стержня)

- момент инерции пули;

- угловая скорость системы после окончания взаимодействия пули со стержнем.

После удара система стержень - пуля совершает крутильные колебания с начальной скоростью. Кинетическая энергия системы, равная:

(+)

согласно закону сохранения энергии перейдет в энергию упругих деформаций т.е.

(+)= (2)

где - наибольший угол поворота стержня;

- постоянная момента упругих сил (коэффициент жесткости)

Из уравнений (I) и (2) получим:

(3)

т.к., то (3) южно переписать в виде:

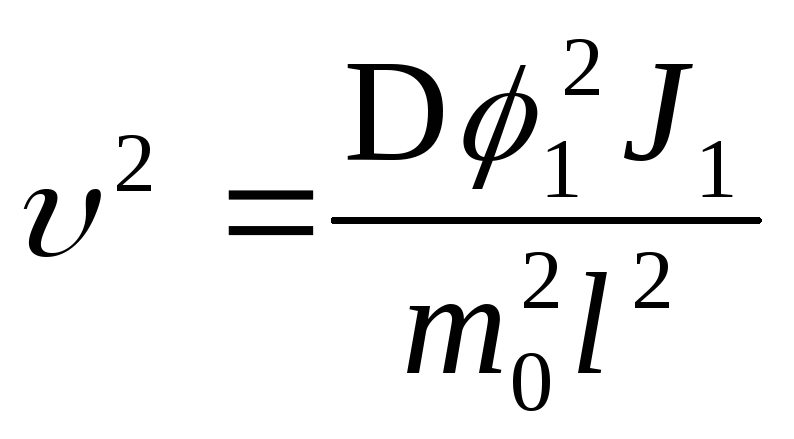(4)

Величины с можно измерить, можно вычислить. Определение на затруднено. Константа может быть исключена. Действительно, в нашем случае система совершает крутильные колебания, которые описываются уравнением движения:

(5)

где - угол поворота стержня (не должен превышать );

- его угловое ускорение;

- момент инерции системы.

Период таких колебаний определяется выражением:

(6)

Меняя положение грузов на стержне (тем самым меняя момент инерции системы), мы изменяем период колебаний маятника:

(7)

где и - период колебаний и момент инерции при одном положении грузов;

и - период колебаний и момент инерции при другом положении грузов.

Из уравнений (7) следует:

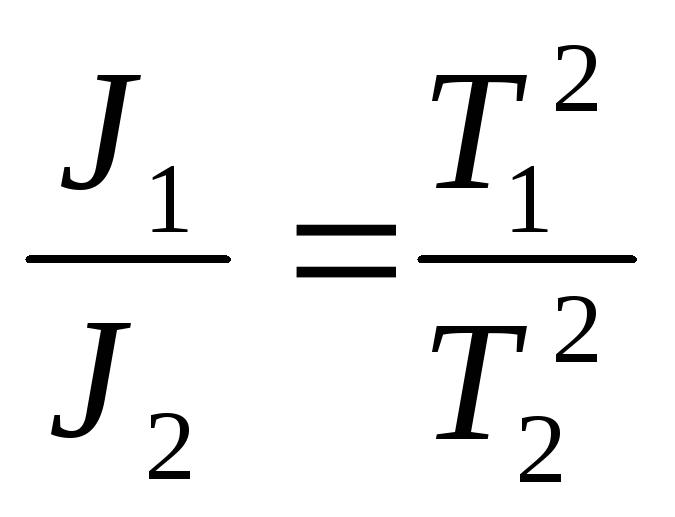(8)

Если характеризует изменение момента инерции системы, то из соотношения (8) можно получив:

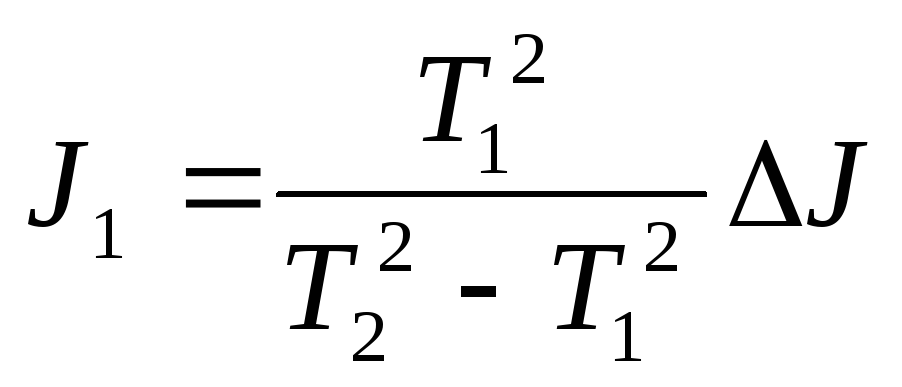(9)

Решая совместно (4), (6) и (9), получим:

(10)

Момент инерции системы при первом положении грузов можно представить в виде:

(11)

а при втором положении грузов:

(12)

где - масса, одного груза;

- момент инерции маятника (стержня) без грузов относительно оси, проходящей через нить подвеса;

- момент инерции груза относительно оси, проходящей через его центр масс;

- расcтояние от центра массы груза до оси вращения при первом положении грузов;

- расстояние от центра массы груза, до оси вращения при втором положении грузов.

При записи значений использована таблица Штейнера. Из (11) и (12) получаем:

(13)

Подставляя в (10), получим окончательное выражение для скорости полета пули:

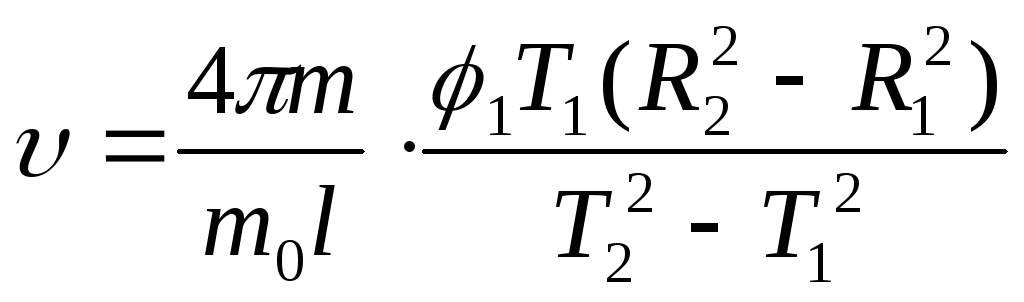(14)

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Баллистический маятник представляет собой настольный прибор (рис. 2), На вертикальной стойке основания 2 крепятся два кронштейна 3. Между верхним и нижним кронштейнами 3 на стальной проволоке закреплен подвес 5, представляющий собой стальной стержень, по которому в горизонтальном направлении перемещаются два груза равной массы. На стержне нанесены деления через 1см. На концах стержня находятся мишени 6 со шкалами. Между верхним и нижним кронштейнами 3 расположен третий кронштейн 7, на котором крепится пусковое устройство, предназначенное для запуска "пули". Конец ствола пусковой устройства и подвес закрыты прозрачным, кожухом 9 на внутренней стороне которого нанесена шкала, предназначенная для определения угла отклонения маятника после выстрела. Снизу кронштейна 7 размещен фотоэлектрический датчик 10, предназначенный для выдачи электрического сигнала на миллисекундомер физический комбинированный 11, позволяющий определить число колебаний и их время t. Миллисекундомер крепится на основании 2 маятника. Стержень 12 совершает колебания вместе с подвесом.

ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА

1. Установить грузы в положение (как можно ближе к оси вращения).

2. Определить , для чего отклонить маятник на угол, не превышающий 10°, нажать кнопку миллисекундомера "ПУСК" и определить время для колебаний (). Вычислить период одного, колеба­ния по формуле: .

3. Измерения по п. 2 повторить три раза. Данные занести в таблицу.

4. Произвести выстрел, определить угол максимального отклонения и расстояние от оси вращения до точки удара пули . Измерения провести три раза. Данные занести в таблицу.

5. Установить грузы в положение (как можно дальше от оси вращения).

6. Определить , для чего проделать все действия по пл. 2-3.

7. Произвести выстрел, определить угол максимального отклонения . Измерения произвести три раза.

8. Вычислить среднее значение .

9. Убедиться, что .

10. По формуле (14) вычислить, скорость пули, выражая радианах ().

Таблица

	(м)					(м)
	(рад)	(c)		(c)	(м)	(рад)	(c)		(c)	(м)
1
2
3
Среднее значение

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Почему в данной работе можно воспользоваться законом сохранения момента импульса?

2. Что называется моментом импульса точки, тела относительно некоторой точки?

3. Выполняется ли закон сохранения механической энергии при абсолютно неупругом ударе пули?

4. Как можно определить момент инерции системы в данной задаче?

5. Доказать, что .

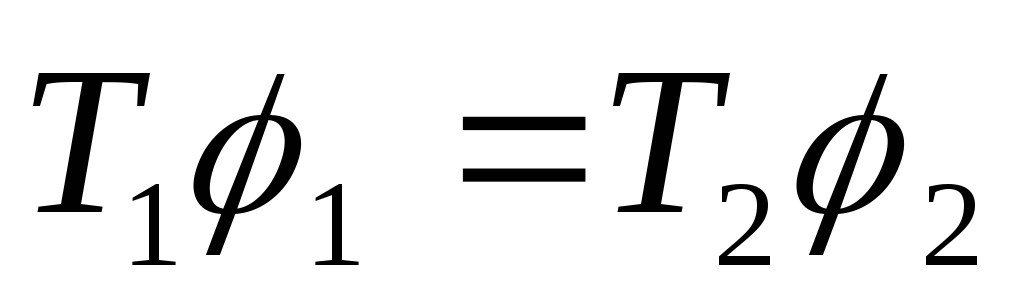6