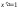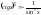9. Границя монотонної варіанти число е.

n’>n=>

n’>n 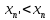-спадна

n’>n -не зростаюча

n’>n -не спадна

Теорема.якщо варіанта монотонна і обмежена зверху, то вона має границю.

Теорема.якщо змінна монотонно спадна і обмежина знизу, то вона має скінченну границю.

Теорема.якщо має скінченну чи нескінченну границю , то таку саму границю має підпослідовність

(обернене твердження незавжди вірне)

Число Ейлера ірраціональне, це неперіодичний, нескінченний дріб який приблизно дорівнює 2,71828…Число Ейлера є границею послідовності lim n-прямує до не скін.(1+1/n)в степені n=е. Число “е”, прийняте за основу системи логарифмів, прийнято називати натуральними. Натуральний логарифм х позначається символом ln x.

10. Лема про вкладені проміжки. [a;b],[a1;b1][an;bn] – сукупність відрізків, таких що a<=a1<=an, b<=b1<=bn – називають системою вкладених відрізків. Яка би не була послідовність вкладених відрізків завжди знайдеться таке число яке належить всім відрізкам. Будь-яка система вкладених відрізків для яких довжина прямує до 0 із зростанням номера n має тільки одне число, яке належить всім цим відрізкам.

13. Означення границі функції на мові послідовностей та на мові «ε-δ».

1.з аніної шпори

(там далі з мого зошита є!)

Означення за Коші. Стале число А будемо наз гран функції f(x) при х прямуючому до а якщо для будь-якого Е>0 існує б>0 таке що |Х-а|<б випливає | f(x) -А|<Е. Означення за Гейне. Число А наз гран функції f(x) при х прямуючому до х0 якщо для будь-якої послідовності {Xn} такої що Хn != Х0 і lim n прямує до нескінченості Хn= Х0 відповідна послідовність {f(Хn) } прямує до А.

2.з мого зошита

Якщо кожному хєХ ставиться уєУ, тона Х задана функція і позначається

у=у(х), у=f(x)

у=g(х) і так далі.

Скінченна а-границя функції f(x)

∀ℇ>0 ∃∂>0 |x-a|<∂=>|f(x)-A|

14. Перша та друга визначні границі.

-перша визначна границя розкриває невизначеність

-друга визначна границя розкриває невизначеність с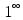

З визначних границь виводяться наслідки:

Де а>0 азокрема, при а=е отримаємо:

17.Означення неперервності функції в точці. Дії над неперервними функціями.

Функцію f(x) наз неперервною в точці а якщо границя функції = знач функції в цій точці лім еф від х=еф від а. Якщо функція неперервна в кожній точці деякого проміжку то вона неперервна на всьому проміжку. Функцію будемо наз неперервною в т а якщо яку б послідовність знач аргумента збіжну до а ми б не взяли то відповідна послідовність знач функції f(x) буде збіжна до f(а). Функцію f(x) будемо називати неперервною в т х=а якщо для будь-якого Е>0 знайдеться б>0 |Х-а|<б випливає | f(x) - f(а) |<Е. Сума, різниця, добуток і частка від ділення двох неперервних функцій також неперервна (для частки – за винятком тих значень аргументів, що перетворюють на нуль знаменник). f(x)* g(x), f(x)+ g(x), f(x)-g(x), f(x)/g(x),

18. Точки розриву та їх класифікація.

Якщо границя функції f(x) в т х=а не існує або =00 або ця границя не рівна знач функції в цій точці то кажуть що функція f(x) в т х=а має розрив.Якщо границя існує то говорять про розрив типу стрибка.Якщо можна покласти f(а)=а і функція стане неперервною то кажуть про поправний розрив.Якщо границя функції в т х=а не існує або =00 то кажуть про розрив другого роду. Монотонно зростаюча(спадна) функція може мати розриви тільки першого роду.

21.Перша і друга теорема Больцано-Коші.

Якщо функція f(x)неперервна на замкненому відрізку [a;b] і на кінцях відрізка приймає різні по знаку значення f(а)* f(б)<0, тоді між а та б знайдеться т с така що f(с)=0 а<c<b. Друга теорема Больцано-Коші. Якщо функція f(x) визначена і неперервна на проміжку [a;b] і приймає різні значення f(а)=А f(б)=В то яке б не було число С, яке знаходиться А<С<В між А і В на проміжку [a;b] знайдеться т с а<c<b така що f(с)=с.

22. Існування оберненої функції.

Якщо кожному елементу з множини У ставиться у відповідність тільки один елемент з множини Х то кажуть що задана обернена функція.ґ=Нехай функція f(x) визначена і строго монотонно зростає та неперервна на деякому проміжку Х тоді на відповідному проміжку У з множини значень функції існує обернена функція яка також є монотонно зростаючою і неперервною.

25.Похідна оберненої функції. Похідні основних елементарних функцій.

Похідні основних елементарних функцій:

Похідна оберненої функції

Похідна елементарної функції є також елементарною функцією.

26.Формули для приросту функції. Зв’язок з диференційованістю і неперервністю функції.

f(б)- f(а)= f'(с) (б-а), хє(а,б) х+дельта х є(а,б), f(х+дельта х)!= f(х) звідси отримуємо формулу скінченних приростів. f(х+дельта х)- f(х)= f'(с)*дельта х. Якщо функція у = f(x) диференційована в деякій точці х0, то вона в цій точці неперервна. 3 цієї теореми випливае, що неперервність функції є необхідною умовою диференційованості функції. Це означае, що в точках розриву функція немає похідної, тобто вона не диференційована.

29. Основні теореми диференціального числення(Ферма, Дарбу, Ролля, Лагранжа, Коші).

Ферма. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку. Якщо вона досягає свого найбільшого чи найменшого значення в якійсь точці х=с є(а,б) то похідна в цій точці =0 f'(с)=0.

Дарбу. Якщо деяка функція на замкнутому відрізку є похідною іншої функції, то на цьому відрізку вона набуває усіх проміжних значень між значеннями на краях відрізка.

Ролля Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку. На кінцях проміжку приймає однакові значення f(а)= f(b) тоді знайдеться т с яка є (а,б) що f'(с)=0. Лагранжа. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку.На кінцях проміжку приймає не рівні значення f(а)=А ,f(б)=В А!=В тоді знайдеться внутрішня точка сє(а,б)така що має місце рівність (f(b)- f(а))/б-а= f'(с).

Коші. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку при чому g’(x)!=0 хє (а,б) тоді знайдеться така точка с є (а,b) що (f(b)- f(а))/ (g(b)- g(а))= f'(с)/ g’(с). Доведення Лагранжа.Розглянемо на проміжку [a;b] наступну функцію:

Перевіримо, що для функції F[x] виконані всі умови теореми Ролля. І справді, F[x] неперервна на проміжку [a;b] та в усіх внутрішніх точках проміжка [a;b] має похідну:

З формули (1) очевидно, що

Згідно з теоремою Ролля на проміжку (а,б) знайдеться точка с така, що

З рівності (2) витікає формула Лагранжа.