Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекція 17-18

.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

333.43 Кб

Скачать

☆

Лекції 17 - 18. Геометричні застосування визначеного інтеграла (площі фігур, довжині ліній, об'єми деяких тіл та площі поверхонь). Деякі фізичні застосування визначеного інтеграла (робота, сила тиску тощо). Різні схеми застосування визначеного інтегрaла

1. Обчислення площ плоских фігур

1.1 Обчислення площ плоских фігур у декартовій системі координат
	[a;b]	задана неперервна функція f (x) ≥ 0 , то, згідно з геометричною
інтерпретацією визначеного інтеграла, площа			криволінійної трапеції, обмеженої кривою
y = f (x) , прямими x = a , x = b та віссю Ox (рис.1), обчислюється згідно з формулою:
S = ∫b	f (x)dx .		(1.1)
a
y	y=f(x)	y
	y=f(x)	a	b
		a	b
		0	x
			y=f(x)
0 a	b x
	Рис.1		Рис.2
	Криволінійні трапеції (рис.1 – при f (x) ≥ 0 , рис.2 – при f (x) ≤ 0 )

Якщо на відрізку [a;b] функція f (x) ≤ 0 (рис.2), то криволінійна трапеція буде розміщена у

нижній півплощині і відповідний визначений інтеграл буде від’ємним. Оскільки площа фігури є величиною невід’ємною, то її можна обчислити згідно з формулою

S =	∫b	f (x)dx	= −∫b	f (x)dx , ( f (x) ≤ 0) .	(1.2)
	a		a
Якщо на відрізку				[a;b] функція f (x)	декілька разів змінює знак (рис.3), то інтеграл на

відрізку [a;b] слід розбити на суму інтегралів по часткових відрізках – відрізках знакосталості функції. Інтеграл буде додатнім на тих відрізках, на яких f (x) ≥ 0 та від'ємним там, де f (x) ≤ 0 . Інтеграл на відрізку [a;b] дає різницю площ фігур, що лежать вище та нижче осі Ox .

y=f(x)

0 a

Рис.3 . Геометрична інтерпретація інтеграла від знакозмінної функції f (x)

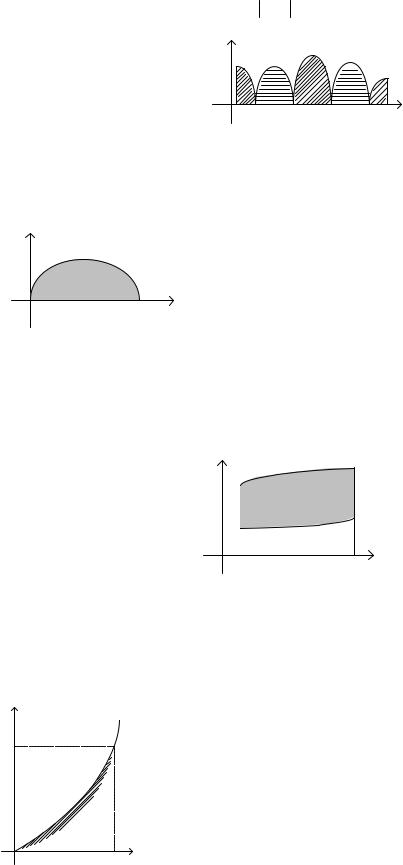
Щоб знайти суму площ без врахування розташування відносно осі Ox , треба знайти суму абсолютних величин інтегралів на відрізках знакосталості функції або обчислити інтеграл від абсолютної величини функції, тобто (рис.4)

S = ∫b		f (x)dx .	(1.3)
	a
y			y=f(x)
			y=f(x)
0	a		b x

Рис.4. Геометрична інтерпретація інтеграла від модуля функції f (x)

Приклад 1.1. Обчислити площу фігури, обмеженої лініями y = sin x та y = 0 на проміжку [0;π].

						Згідно з формулою (1.1) для невід'ємної на			[0, π] функції
y				y=sinx		y = sin x матимемо
1				y=sinx		π		π =1 +1 = 2 (кв.од.) .


						S = ∫sin xdx = −cos x
						o		0
								0

0			π/2		π	x
Якщо треба			обчислити			площу фігури,	розміщеної між лініями y = f1 (x) ,		y = f2 (x) та
прямими x = a ,			x = b		( f1 (x) ≤ f2 (x) на відрізку [a;b]) (рис.5), то формула площі запишеться
S = ∫b		f2 (x)dx −∫b			f1 (x)dx = ∫b (f2 (x) − f1 (x))dx .				(1.4)
	a			a		a
						y	y=f2(x)

y=f1(x)

b x

Рис.5.

Приклад 1.2. Обчислити площу фігури, обмеженої параболами y = x2 ; y =

Розв’язуючи систему рівнянь

y = x2

, знаходимо абсциси точок

y =

перетину:

x1 = 0 ;

=3 .

Вважаючи

f1 (x) =

, f 2 (x) = x

на підставі формули (1.4) отримаємо

(кв.од.).

S = ∫ x

−

dx =

−

= =

9 −

y=x2

y=x3/3

3 x

1.2. Обчислення площ фігур, що обмежені лініями, заданими параметрично.

Якщо необхідно обчислити площу криволінійної трапеції, обмеженої лінією, що задана у параметричній формі

x = x(t) , y = y(t) ,

(1.5)

де α ≤ t ≤ β , x(α) = a ,

x(β) =b ,

то у формулі S = ∫b

f (x)dx = ∫b ydx

перейдемо до нової змінної,

беручи за незалежну змінну t .

′

З рівняння (1.5) маємо dx = x (t)dt і

S = ∫y(t)x′(t)dt .

(1.6)

Це формула для обчислення площі криволінійної трапеції, обмеженої лінією, що

задана параметрично.

Приклад 1.3. Обчислити площу еліпса x = acost ,

y = bsin t .

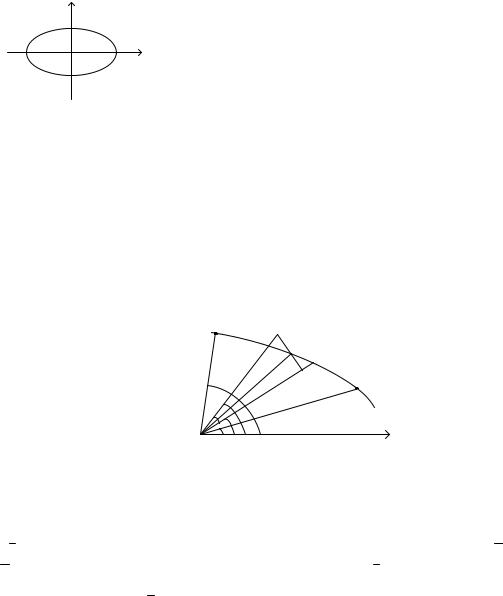
Площу еліпса будемо обчислювати як подвоєну площу його

верхньої половини (див. рис.), для якої

x змінюється від −a

до

a ,

-a

x отже параметр t

набуває

значень

від

π до 0 .

Враховуючи,

що

-b

dx = −a sin tdt

, матимемо

sin 2t

π =πab .

S = 2∫b sin t (−a sin t)dt =

2ab∫sin

tdt = ab∫(1 − cos 2t)dt =

−

= ab

= ab t

(Якщо a = b = r , то еліпс перетворюється в коло і площа відповідного круга дорівнює πr2 ).

1.3. Обчислення площ у полярній системі координат

Нехай у полярній системі координат є крива, задана рівнянням

r = r(ϕ) ,

(1.7)

де r(ϕ) -– неперервна функція при α ≤ϕ ≤ β .

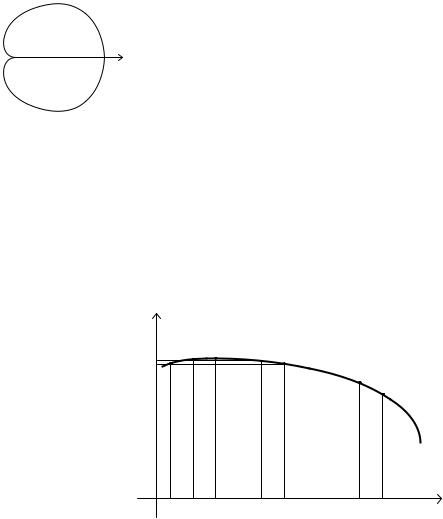
Обчислимо площу сектора

AOB , обмеженого кривою r = r(ϕ)

і променями ϕ =α ,

ϕ = β

(рис.6)

Δϕi

ϕi-1

Рис.6

Розіб’ємо сектор AOB

на

частин променями ϕ =α , ϕ =ϕ1 ,

ϕ =ϕ2 ,…, ϕ =ϕn−1 ,

ϕ = β

(α < ϕ1

< ϕ2

< ... < ϕn−1 < β) . Позначимо через

ϕi

кут між проведеними променями ϕi−1

і ϕi , а

через

–

довжину

радіус-вектора точки,

що

відповідає

деякому куту

ϕi , такому,

що

ϕi −1 <

ϕi

<ϕi

. Розглянемо круговий сектор OCD з радіусом

і центральним кутом

ϕi

, його

площа

дорівнює

. Сумуючи

ці

площі

для

всіх

значень

i ( i =1,2,..., n ),

2 i

отримаємо площу ступінчастої фігури

Sn = ∑ Si =

ϕi =

ϕi .

∑ri

∑(r(ϕi ))

i=1

2 i=1

Ця сума є інтегральною для функції

r2 (ϕ) на відрізку α ≤ϕ ≤ β ;

її границя при

ϕi

→ 0 є

визначеним інтегралом

								β
						S = 12 ∫r 2 (ϕ)dϕ .																		(1.8)
								α
Приклад 1.4. Обчислити площу фігури, обмеженої кардіоїдою r =1+cosϕ .
	Складемо таблицю значень функції r = r(ϕ) для окремих значень аргумента

ϕ		0		± π			± π				± π			± 2π			± 5π				±π
ϕ
				6			3				2
				6			3				2				3			6
r(ϕ)		2		≈1,9			1,5		1					0,5			≈ 0,1				0

							і по цих точках побудуємо наближено кардіоїду.
							Оскільки кардіоїда, очевидно, симетрична відносно полярної осі, то її
0		1		2			площа дорівнює подвоєній площі її верхньої половини і обчислюється:
										1	π			π
							S = 2			1	∫r 2 dϕ = ∫(1 + cosϕ)2 dϕ =
							S = 2		2		∫r 2 dϕ = ∫(1 + cosϕ)2 dϕ =
									2		0	0
											0	0
							π
							= ∫(1 + 2 cosϕ + cos 2 ϕ)dϕ =
							0
	π		π	π 1	+ cos 2ϕ							1			1				π		π		3π
	π		π	π 1	+ cos 2ϕ							1			1				π		π		3π
= ϕ	0	+ 2sin ϕ	0	+ ∫				dϕ	= π +				ϕ +			sin 2ϕ			0	= π +		=		.
= ϕ		+ 2sin ϕ		+ ∫				dϕ	= π +				ϕ +			sin 2ϕ				= π +		=		.
				0	2							2			2						2		2
					2							2			2						2		2

2.Обчислення довжини дуги кривої

2.1.Обчислення довжини дуги у декартовій системі координат

Нехай крива на площині задана рівнянням y = f (x) . Знайдемо довжину дуги AB цієї

кривої, обмеженої прямими x = a ,	x = b (рис.7).
y
yi A M1	M2 Mi-1 Mi
	Mn-1	B
		B
		y=f(x)

	a x1		x
0	a x1	x2	xi-1 i xi	xn-1 b	x
	Рис.7. Знаходження довжини дуги
Виберемо на AB послідовно		точки	A = M 0 , M1 , M 2 , ..., M i−1 ,		M i , .., M n = B з абсцисами
x0 = a, x1, x2 ,..., xi−1, xi ,..., xn−1 , xn = b відповідно та проведемо хорди					AM1 , M1M 2 , …, Mi −1Mi ,…,
M n−1B , довжини яких позначимо		l1 , l2 ,…, li ,…,		ln . Одержимо ламану лінію, вписану в
дугу AB ; її довжиною є
n
l = ∑ li .				(2.1)
i=1
Означення 2.1. Довжиною l	дуги AB називають границю, до якої прямує довжина вписаної
					n

ламаної, коли довжина її найбільшої частини прямує до нуля, тобто l = maxliml →0 ∑ li .
i	i=1

(Тут і надалі ми припускаємо, що така границя існує).

Теорема 2.1. Якщо на відрізку [a;b]

функція

′

f (x) та її похідна f (x) неперервні, то довжина

дуги кривої y = f (x) , обмеженої x = a та x = b , обчислюється згідно з формулою

l = ∫

′

= ∫

′ 2

dx .

(2.2)

1+(y (x))

1+(y )

˛ Як видно з рис.7, згідно з теоремою Піфагора

xi .

li =

( xi )

+( yi )

Згідно з теоремою Лагранжа маємо

yi =

f (xi ) − f (xi−1 )

= f ′(ξi ) ,

де xi −1 ≤ξi ≤ xi .

Отже, li

1+( f ′(ξi ))2

xi . За умовою теореми функція

f ′(x) неперервна, тому неперервною

є і функція

′

(x))

, звідки випливає, що існує скінчена границя

1+( f

l = maxlimx →0 ∑ 1+( f ′(ξi ))2

xi = maxlimx →0 ∑ 1+( f ′(xi ))2

xi =

i=0

= ∫

1+( f '(x))

= ∫

′ 2

dx .

1+( y )

Приклад 2.1. Обчислити довжину дуги лінії y = ln(1 − x 2 )

від точкиx = 0

до точкиx =

−2x

Знайдемо y′

і, підставляючи у (2.2), дістанемо

1− x2

−2x 2

4x2

1 −2x2 + x4 + 4x2

dx =

l = ∫ 1

− x

dx = ∫ 1 +

(1 − x

)

2 dx = ∫

)

(1 − x

(1 + x2 )2

1 + x2

−1

+ 2

= ∫

2 dx =

∫

2 dx = −∫

dx = −∫

1 +

dx =

− x

)

− x

−1

x −1

+ ln

−

+ 0 = −

− ln

= ln 3 −

= − x + ln

x +1

= −

2.2. Обчислення довжини дуги лінії, заданої параметрично

Знайдемо довжину дуги кривої, якщо її рівняння задано параметрично

x =ϕ(t) ,	y =ψ(t) (α ≤ t ≤ β) ,	(2.3)
де ϕ(t) , ψ(t) –		′		не перетворюється в нуль
	неперервно диференційовні функції, причому ψ		(t)

на [α; β].

Тоді у формулі (2.2) врахуємо, що dx =ϕ′(t)dt , dy

x = a при t =α і x = b при t = β , то

	l = ∫b	β
	l = ∫b	1+( y′)2 dx = ∫
Отже,	a	α
Отже,
β	β
l = ∫ (ϕ′(t))2 +(ψ′(t))2 dt = ∫ (x′(t))2 +( y′(t))2 dt .
α	α

′

(t)dt

(t)

=ψ (t)dt ;

і якщо

′

ϕ (t)dt

ϕ (t)

′

ψ (t)

dt .

ϕ′(t)

ϕ (t)dt = ∫

(ϕ (t))

+(ψ (t))

(2.3)

Приклад 2.2. Знайти довжину астроїди x = acos3 t , y = asin3 t , 0 ≤t ≤ 2π .

Оскільки астроїда симетрична відносно координатних осей, то

достатньо знайти чверть її довжини, що відповідає зміні параметра t

від 0 до π .

-a

a x

x (t) = −3a cos

t sin t ,

y (t) =3a sin

t cost , матимемо

Враховуючи, що

′

-a

l = 4∫2

(−3a cos2 sin t)2 +(3asin2 t cost)2 dt = = 4∫2

9a2 cos4 t sin 2 t + 9a2 sin 4 t cos2 t dt = 4∫2

3a sin t cos tdt =

= 6a .

=12a ∫sin td (sin t) = 6asin 2 t

2.3. Обчислення довжини дуги у полярній системі координат

Нехай у полярній системі координат задано рівняння лінії

r = r(ϕ) ,

(2.4)

де r – полярний радіус,

– полярний кут, α ≤ϕ ≤ β . Запишемо формули переходу від

полярних до декартових координат x = r cosϕ ,

y = r sinϕ

або, враховуючи, що r = r(ϕ) :

x = r(ϕ)cosϕ ,

y = r(ϕ)sinϕ .

(2.5)

Ці рівняння можна розглядати як параметричне (відносно ϕ ) рівняння лінії, для обчислення

її довжини використаємо формулу (2.3) з врахуванням того,що: x′ = (r(ϕ) cosϕ)′ = r′(ϕ) cosϕ −r(ϕ) sin ϕ = r′cosϕ −r sin ϕ ,

y′ = (r(ϕ) sin ϕ)′ = r′(ϕ) sin ϕ + r(ϕ) cosϕ = r′sin ϕ + r cosϕ .

Отже,

ββ

l = ∫ (x′)2 +( y′)2 dϕ = ∫

(r′cosϕ −r sinϕ)2 +(r′sinϕ +r cosϕ)2 dϕ =

= ∫

(r′)2 cos2 ϕ +r 2 sin2 ϕ −2rr′sinϕcosϕ +(r′)2 sin 2 ϕ +

+r 2 cos2 ϕ +2rr′sinϕcosϕ

dϕ = ∫

(r′)2 +r 2 dϕ .

Таким

чином,

довжина

дуги

лінії

r = r(ϕ) ,

обмеженої променями ϕ =α , ϕ = β ,

обчислюється згідно з формулою

l = ∫

(r′)2 +r 2 dϕ .

(2.6)

Приклад 2.3. Обчислити довжину першого витка спіралі Архімеда r =ϕ , 0 ≤ϕ ≤ 2π .

Скористаємось формулою (2.6),

враховуючи, що r′=1 та використаємо формулу (3.7)

розділу 6.

2π

1 +ϕ

+ϕ

ln ϕ +

1 +ϕ

2π

l = ∫

dϕ =

=π 1 + 4π

+ ln 2π + 1 + 4π 2 .

3.Обчислення об’єму тіла

3.1.Обчислення об’єму тіла за відомими поперечними перерізами

Нехай дано деяке тіло T і відома площа довільного перерізу цього тіла площиною, перпендикулярною до осі Ox (рис 8); вона є неперервною функцією від x : S = S(x) .

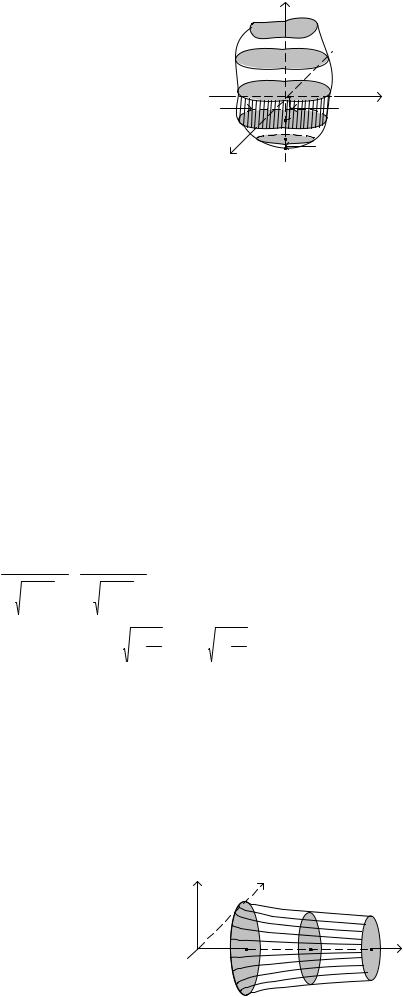
x b

Vi	xi-1	xi z

y	a	x1

Рис.8. Тіло T	та його поперечні перерізи

Проектуючи тіло на вісь Ox , отримаємо відрізок [a;b]. Розіб’ємо його на велику кількість

малих

частин

( i =1,2,...,n )

через

точки

поділу

x1 , x2 , ..., xn

проведемо

площини,

перпендикулярні до осі Ox . В результаті тіло складатиметься з n шарів,

кожен з яких

наближено можна вважати циліндром.

Оскільки об’єм i -го шару наближено дорівнює

Vi ≈ S(ξi )

xi , де

xi−1 <ξ < xi , то, сумуючи

об’єми всіх шарів, матимемо об'єм ступінчастого тіла

Vn = ∑S(ξi ) xi .

i=1

Якщо n →∞ ,

причому max xi

→ 0 , то об'єм Vn

прямує до об'єму тіла T і

V = maxlimx →0 ∑S(ξi )

= ∫S(x)dx .

(3.1)

i=1

Приклад 3.1. Обчислити об’єм еліпсоїда

=1 .

Перетинаючи еліпсоїд площиною,

паралельною до площини YOZ

і розміщеною на відстані

від неї, отримаємо еліпс

=1−

; або

y 2

z 2

=1 .

1 −

c 1

−

Його півосі

= b

1 − x2

c1 = c

1 − x2

. Площа цього еліпса (див. приклад 1.3) пропорційна

добутку півосей:

S(x) =πb1c1 =πbc 1 −

. Обчислимо об’єм еліпсоїда згідно з формулою (3.1):

πabc .

V =πbc ∫ 1 −

dx =πbc x

−

− a

−a

Зокрема, якщо a = b = c = r , то еліпсоїд перетворюється в кулю, об’єм якої V =

πr3 .

3.2. Обчислення об’єму тіла обертання

Знайдемо об’єм V

тіла, отриманого обертанням навколо осі Ox

криволінійної трапеції,

обмеженої неперервною

лінією y = f (x)

( f (x) ≥ 0 ),

відрізком

[a;b] осі

і двома

вертикалями x = a і x = b (рис. 9).

y=f(x)

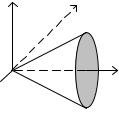
Рис.9. Тіло, отримане обертанням неперервної лінії навколо осі Ox

Ця задача є частковим випадком попередньої, коли поперечним перерізом, що відповідає абсцисі x , є круг радіуса r = f (x) з площею S =πr2 =π f 2 (x) .

Отже, згідно з формулою (3.1),

V = ∫b πf 2 (x)dx =π∫b		f 2 (x)dx .	(3.2)
a	a
Якщо тіло	утворилось обертанням навколо осі Oy		криволінійної трапеції, обмеженої

неперервною лінією x = g( y) , ( g( y) ≥ 0 ), відрізком c ≤ y ≤ d осі Oy і паралельними прямими y = c і y = d , то його об’єм дорівнює

V =π∫d g 2 ( y)dy .

Приклад 3.2. Відрізок прямої, що сполучає початок координат з точкою навколо осі Ox . Знайти об’єм конуса, що утворився.

(3.3)

A(a;b) обертається

z	y	Запишемо рівняння прямої OA :			y =	b		x
						a
b	A	a	b	2			πb2

		згідно з формулою (3.3): V =π∫		x	dx =			a	2

0		0	a

	a	x

та обчислимо об’єм конуса

x3	a	=	πb2a	.
3	0		3

4. Застосування визначеного інтеграла в економічних задачах

4.1. Витрати, дохід та прибуток

Нехай TC(x) – функція загальних витрат виробництва x одиниць продукції,

′	– функція граничних витрат (див. розділ 3). Тоді визначений інтеграл
MC(x) =TC (x)
∫b MC(x)dx =TC(b) −TC(a)		(4.1)
a

дорівнює зміні загальних витрат при зростанні обсягу виробленої продукції від a до b одиниць.

За аналогією, якщо MR(x) – функція граничного доходу (виторгу), то зміна доходу при зростанні реалізації виробленої продукції обчислюються згідно з формулою

∫b MR(x)dx =TR(b) −TR(a) ;	(4.2)
a		x – кількість
Приклад 4.1. Функція граничного доходу задається формулою R (x) =10 −0,02x , де		x – кількість
	′

проданих одиниць продукції.

а) Визначити загальний дохід від продажу 300 одиниць товару.

б) Яким буде додатковий дохід, зумовлений зростанням продажу від 200 до 300 одиниць? а) За формулою (4.2), при реалізації 300 одиниць товару дохід становитиме

300	300	= 3000 −900 = 2100 (грн.).
∫ (10 −0,02x)dx = (10x −0,01x2 )	300	= 3000 −900 = 2100 (грн.).
0	0
	0

б) При зростанні продажу від 200 до 300 одиниць продукції додатковий дохід дорівнюватиме

300	300
∫ (10 − 0,02x)dx = (10x − 0,01x 2 )	300	= (3000 − 900) − (2000 − 400) =
200	200
	200

= 2100 −1600 =500 (грн.).

4.2. Поточна вартість грошових потоків

При аналізі альтернативних варіантів використання фінансових коштів, порівнянні привабливості інвестиційних проектів тощо широко використовують поняття поточної

вартості. Поточна вартість – це сьогоднішня вартість доходу, який буде отримано у майбутньому. Поточна вартість враховує процент, який можна заробити за період від сьогодні до деякого моменту у майбутньому. Якщо процентна ставка дорівнює r , то поточну вартість неперервного потоку доходу постійної величини A упродовж n років можна знайти як

PV = ∫n Ae−rt dt .

Приклад 4.2. Компанія повинна обрати одну з двох можливих стратегій розвитку: 1) вкласти

10млн.грн. у нове обладнання і одержувати 3 млн. грн. прибутку щорічно упродовж 10 років;

2)придбати досконаліше обладнання, інвестувавши 15 млн.грн., що дасть змогу отримувати щорічно 5 млн.грн. прибутку протягом 7 років. Яку стратегію варто обрати, якщо, як оптимістично вважають експерти компанії, процентна ставка залишатиметься на рівні 10%?

Увипадку обрання першої стратегії чистий приведений дохід компанії (поточна вартість майбутніх прибутків мінус інвестиційні витрати) становитиме:

π1

∫

−0,1t

dt −10 = −30e

−0,1t

−10

−

−10 =8,964

млн.грн.

=30 1

Для другої стратегії матимемо:

π2

= ∫7

5e−0,1t dt −15 =50(1 − e−0,7 )−15

=10,17 млн.грн.

Отже, фірма повинна обрати другу стратегію (але все ж задуматися щодо адекватності оцінки ситуації своїми експертами).

Соседние файлы в папке 2. Лекції

#
12.02.2016370.63 Кб40Лекції 22 - 23.pdf
#
12.02.2016389.41 Кб55Лекції 9-10.pdf
#
12.02.2016436.41 Кб114Лекція 1.pdf
#
12.02.2016377.09 Кб44Лекція 11.pdf
#
12.02.2016379.34 Кб42Лекція 15-16.pdf
#
12.02.2016333.43 Кб41Лекція 17-18.pdf
#
12.02.2016320.45 Кб54Лекція 19.pdf
#
12.02.2016280.94 Кб53Лекція 2.pdf
#
12.02.2016311.55 Кб39Лекція 20.pdf
#
12.02.2016320.03 Кб43Лекція 21.pdf
#
12.02.2016323.33 Кб40Лекція 24.pdf