Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекція 15-16

.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

379.34 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекції 15 -16. Визначений інтеграл, означення, властивості. Практичне тлумачення, прості практичні задачі. Похідна інтеграла зі

змінною верхньою межею. Формула Ньютона –Лейбніца. Стандартна техніка визначеного інтегрування. Оцінки інтегралів. Інтегрування з застосуванням таблиць та пакетів програм

1. Означення та властивості визначеного інтеграла
1.1.Задача про знаходження площі криволінійної трапеції
Історично поняття первісної функції тісно пов'язане з задачею про знаходження площі
фігури.
Нехай на проміжку [a,b] задана неперервна функція y = f (x) , що набуває лише невід'ємних
значень (рис.1).
y					y=f(x)
M					y=f(x)
M					C
	B				C
yi	B
yi
m
	Aa x1			xi	xn-1 b D
0	Aa x1	xi-1	ξ	xi	xn-1 b D	x
			i
Рис.1. Криволінійна трапеція та її площа.

Розглянемо фігуру ABCD , що обмежена кривою y = f (x) , вертикалями x = a, x = b і відрізком [a; b] осі OX – така фігура називається криволінійною трапецією. Поділимо її основу довільними точками a = x0 , x1 , ..., xn = b на n частин, причому x0 < x1 <... < xn і введемо

позначення x1 = x1 − x0 ; x2 = x2 − x1 ; xn = xn − xn−1 .

Якщо через точки поділу провести вертикальні лінії, то трапеція ABCD розіб'ється на n криволінійних трапецій. Замінимо тепер наближено кожну трапецію деяким прямокутником, основа якого така ж як у трапеції, а висота збігається з ординатою однієї із точок лінії

yi = f (ξi ) . Тоді площа криволінійної трапеції S наближено може бути замінена площею деякої ступінчатої фігури, складеної з окремих прямокутників

Sn = ∑n	yi xi = ∑n	f (ξi ) xi .
i=1	i=1

Якщо всі довжини xi прямують до нуля, то різниця між точним S і наближеним Sn значеннями площі трапеції S − Sn також наближається до нуля.

Отже, точним значенням площі можна вважати

S = lim S

= lim

∑

= lim

∑

f (ξ

)

→0

n→∞

i=1

Зауваження. Для позначення граничного значення такої суми Лейбніц ввів символ ∫ydx , де ydx нагадує типовий доданок суми (1.1), а знак ∫ є стилізованою буквою S – початковою буквою латинського слова "Summa" . Оскільки площа, що представляє це граничне значення, тісно пов’язана з первісною функції y = f (x) , то символ ∫ зберігається і для сукупності усіх

первісних. Враховуючи зв'язок між знаходженням площ плоских фігур та їх квадратурою, саме знаходження інтегралів часом називають квадратурою.

Для того, щоб сказане вище могло поширюватись і на функції, що приймають і від'ємні значення, достатньо домовитись вважати від'ємними площі частин фігури, розміщених під віссю OX .

1.2. Означення визначеного інтеграла та умови його існування

Враховуючи наведені вище позначення, введемо означення визначеного інтеграла.

Означення 1.1. Число δ =max xi називається діаметром розбиття.

i=1,n

На кожному з відрізків [x0 ; x1 ], [x1; x2 ],…, [xn−1; xn ] виберемо по точці, які позначимо ξ1 ,ξ2 ,...,ξn (x0 <ξ1 <ξ2 < ... <ξn < b) і складемо суму

Sn	= f (ξ1 ) x1 + f (ξ2 ) x2 +... + f (ξn ) xn = ∑n	f (ξi )	xi .	(1.1)
	i=1			на відрізку [a;b].
Ця сума називається інтегральною сумою функції			f (x)	на відрізку [a;b].
Сума Sn	залежить від способу розбиття відрізка [a;b] на частини [xi−1 ; xi ] і від вибору точок

ξi на кожному з цих відрізків. Виберемо такі розбиття, діаметри яких прямують до нуля (при

цьому, очевидно, кількість відрізків n прямує до безмежності). Для кожного з розбиттів складемо інтегральну суму (1.1). Припустимо, що при δ → 0 (при цьому n →∞) границя

послідовності часткових сум Sn прямує до деякого числа S : limSn = lim∑n		f (ξi ) xi = S .
δ→0	δ→0 i=1

Означення 1.2. Якщо для довільних розбиттів відрізка [a;b], діаметри δ яких прямують до нуля, і для довільного вибору точок ξi на відрізках [xi−1; xi ] інтегральна сума

Sn = ∑n		f (ξi ) xi прямує до одного і того ж числа S , то це число називається
	i=1
визначеним інтегралом функції f (x)				на відрізку [a;b] і позначається ∫b	f (x)dx .
				a
Тобто
∫b	f (x)dx = lim∑n		f (ξi ) xi ,		(1.2)
a		δ→0 i=1
a називається нижньою межею інтеграла, b – верхньою межею; [a;b] – відрізок
інтегрування, x – змінна інтегрування.
Означення 1.3. Якщо для функції f (x) границя (1.2) існує, то функція називається
інтегровною на відрізку [a;b].

Необхідною умовою існування визначеного інтеграла (1.2) на відрізку [a;b] є обмеженість функції y = f (x) на цьому відрізку. Дійсно, якщо функція була б необмеженою, то за рахунок вибору точки ξ можна зробити значення f (ξ) , а разом з ним і суму як завгодно великою. За

цих умов скінченної границі для S , очевидно, не існувало б. Тому надалі вважатимемо, що розглядувані функції є обмежені, тобто m ≤ f (x) ≤ M .

1.3. Суми Дарбу та їх властивості

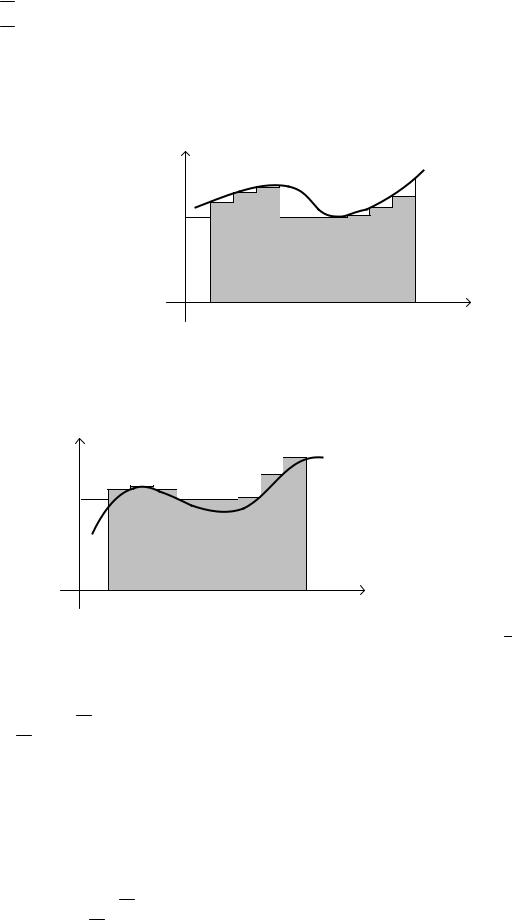
Позначимо через m і M найменше і найбільше значення функції f (x) на відрізку [a, b]. Найбільше і найменше значення функції f (x) на кожному з інтервалів [xi−1; xi ] (i =1, n) позначимо M i і mi відповідно. Побудуємо суми

Sn = m1	x1 + m2	x2 +... + mn xn		= ∑n	mi xi ;
				i=1
Sn = M1	x1 + M 2 x2 +... + M n xn = ∑n					M i	xi ,
				i=1
які називаються нижньою і верхньою інтегральними сумами Дарбу.
Для невід’ємної функції ( f (x) ≥ 0) вони мають такий зміст (рис.2, 3): нижня інтегральна
сума Дарбу чисельно дорівнює площі ступінчастої фігури з вертикалями x = x0 , x = x1 ,…,
x = xn , що вписана в криволінійну трапецію, обмежену лініями y = f (x) , y = 0 , x = a , x = b .
			y						y=f(x)
			mi
			0	a x1			xi-1	xi	xn-1 b	x
		Рис.2. Геометрична інтерпретація нижньої суми Дарбу Sn
За аналогією, верхня інтегральна сума Дарбу чисельно дорівнює площі ступінчастої фігури
(рис.3) з вертикалями x = x0 ,				x = x1 ,…,			x = xn , описаної навколо криволінійної трапеції, що
обмежена лініями x = a ,			x = b , y = 0 ,				y = f (x) .
	y						y=f(x)
	Mi
	0	a x1	xi-1			xi	xn-1 b	x

Рис.3. Геометрична інтерпретація верхньої суми Дарбу Sn

Нижня та верхня інтегральні суми мають такі властивості:

1. Sn ≤ Sn ≤ Sn .

˛ Оскільки для довільної точки ξi

з відрізку [xi−1

; xi ] справедливою є нерівність

mi ≤ f (ξi ) ≤ M i , а, отже, і mi xi

≤ f (ξi ) xi ≤ M i

( xi > 0) , то

∑n

mi xi ≤ ∑n

f (ξi ) xi ≤ ∑n

M i

xi .

i=1

Оскільки ∑n

= Sn , ∑n

M i

xi =

, ∑n

f (ξi )

xi = Sn , матимемо Sn ≤ Sn ≤

i=1

2. m(b − a) ≤ Sn ≤ Sn ≤ M (b − a) (довести самостійно).

1.4. Умова існування визначеного інтеграла

За допомогою сум Дарбу можна сформулювати умову існування визначеного інтеграла.

Теорема 1.2. Для існування визначеного нтеграла необхідно і достатньо, щоб

lim(Sn − Sn ) =0 .

δ→0

Вкажемо декілька класів інтегровних функцій.
1.	Якщо функція	f (x)	неперервна на [a,b], то вона інтегровна на цьому відрізку.
2.	Якщо функція	f (x)	неперервна на [a,b] всюди за виключенням	скінченної кількості
	точок, які є точками розриву першого роду, то вона інтегровна на цьому відрізку.
3.	Якщо функція	f (x) монотонна і обмежена на [a,b], то вона інтегровна на цьому відрізку.

2.Геометричний та фізичний зміст визначеного інтеграла

2.1.Геометричний зміст визначеного інтеграла

Для невід’ємної функції y = f (x) інтеграл ∫b	f (x)dx	чисельно дорівнює площі криволінійної
a
трапеції, обмеженої лініями x = a , x = b , y = f (x) ,		y = 0 (див. п. 1.1).

2.2. Фізичний зміст визначеного інтеграла

Задача. Знаючи швидкість v = v(t) прямолінійного руху точки, знайти шлях, пройдений нею

за проміжок часу 0 ≤ t ≤ T .

Напрямляючи вісь Ox вздовж руху точки і вважаючи x = x(t) рівнянням її руху, матимемо:

v(t) =		dx	, звідки dx = v(t)dt . Інтегруючи обидві частини рівності в межах від		0 до T ,
v(t) =					0 до T ,
		dt
знайдемо відповідний шлях S = x(T ) − x(0) = T∫v(t)dt .
				0
	3. Основні властивості визначеного інтеграла
	3.1.Властивості, що виражаються рівностями
1. Величина визначеного інтеграла не залежить від змінної інтегрування: ∫b					f (x)dx = ∫b	f (t)dt .
				a	a
2. При зміні порядку інтегрування знак інтеграла змінюється на протилежний:
∫b	f (x)dx = −∫a			f (x)dx .

Зцієї властивості випливає, що

∫a	f (x)dx = 0 .	(3.1)
a
3. Сталий множник можна виносити за знак інтеграла:
∫b Af (x)dx = A∫b		f (x)dx .

4.Якщо f (x) і g(x) інтегровні на [a;b], то сума f (x) + g(x) також інтегровна на [a;b],

причому

∫b ( f (x) + g(x))dx = ∫b			f (x)dx + ∫b g(x)dx .
a		a		a
5. Якщо f (x) інтегровна на [a; c] і [c;b], то вона інтегровна і на [a;b], причому
∫c	f (x)dx + ∫b	f (x)dx = ∫b		f (x)dx .
a	c		a

Зауваження. Точка c може бути розміщена довільно щодо a,b .

3.2.Властивості, що виражаються нерівностями

Вкажемо декілька властивостей визначених інтегралів, що виражаються нерівностями, причому вважаємо, що a < b .

Якщо

f (x) інтегровна на [a;b] і f (x) ≥ 0 , то ∫b

f (x)dx ≥ 0 .

f (x) інтегровна на [a;b], то функція

також інтегровна на [a;b], причому

Якщо

f (x)

∫b

f (x)dx ≤ ∫b

f (x)

dx .

f (x) неперервна на [a;b] і M

Якщо функція

та m –- її найбільше і найменше значення на

цьому відрізку, то

m(b −a) ≤ ∫b

f (x)dx ≤ M (b −a) .

(3.2)

Якщо

f (x) і g(x) інтегровні на [a;b], і f (x) ≤ g(x) на цьому відрізку, то ∫b

f (x)dx ≤ ∫b g(x)dx .

Приклад 3.1. Вияснити (не обчислюючи), який з інтегралів більший: ∫1 x3 cos2 xdx чи ∫1 x2 cos2 xdx .

											0			0
	Оскільки x3 ≤ x2 при 0 ≤ x ≤1 та cos2 x ≥0 , то x3 cos2 x ≤ x2 cos2 x і, згідно з властивістю 4,
										1	1
другий інтеграл не менший за перший, тобто ∫x3 cos2 xdx ≤ ∫x2 cos2 xdx .
										0	0
Приклад 3.2. Оцінити інтеграл								2∫π	dx	.
Приклад 3.2. Оцінити інтеграл								2∫π	11 + 3 cos x	.
								0
											1		набуває при x =π , коли
	Найбільшого значення підінтегральна функція f (x) =
	Найбільшого значення підінтегральна функція f (x) =											11 + 3 cos x
косинус дорівнює −1 і знаменник мінімальний, тобто M = f (π) = 1 .
											8
За аналогією, при x =0						та x = 2π		підінтегральна функція набуваає найменшого значення:
m = f (0) = f (2π) =				1	.
m = f (0) = f (2π) =		14			.
		14
Отже, 1 ≤ f (x) ≤		1			на відрізку [0; 2π], звідки, враховуючи властивість 3 ( b − a = 2π ) , матимемо:
Отже, 1 ≤ f (x) ≤		14
	8	14
1	2π		1				π	2π	dx		π .
1	2π ≤ ∫ f (x)dx ≤		1		2π	або	π	≤ ∫	dx	dx ≤	π .
8	0	14					4	0	11 +3cos x		7
	0							0
Теорема про середнє. Якщо функція									f (x) неперервна на [a;b], то на цьому відрізку
знайдеться така точка ξ , для якої виконується співвідношення
∫b	f (x)dx = f (ξ)(b −a) .
a

˛ Нехай a < b . Тоді, якщо m і M є відповідно найменшим і найбільшим значенням функції

f (x) на відрізку [a;b], то, згідно з (3.2),				m ≤	1	∫b	f (x)dx ≤ M .
f (x) на відрізку [a;b], то, згідно з (3.2),				m ≤	b −a	∫b	f (x)dx ≤ M .
Позначимо						a
Позначимо
	1	∫b	f (x)dx = μ ,				(3.3)
	b − a	∫b	f (x)dx = μ ,				(3.3)
		a

де m ≤ μ ≤ M .

Оскільки функція f (x) неперервна на [a;b], то на цьому відрізку вона набуває всіх проміжних значень між m і M , тобто знайдеться така точка ξ , що μ = f (ξ) і, згідно з (3.3),

∫b	f (x)dx = f (ξ)(b −a) .
a
Означення 3.1. Число
f (ξ) =		1	∫b	f (x)dx	(3.4)
		b −a
			a		f (x) на відрізку [a; b].
називається середнім значенням функції

Геометрична інтерпретація теореми про середнє. Площа криволінійної трапеції, що обмежена неперервною лінією y = f (x) на відрізку [a;b], рівновелика площі прямокутника з

тією ж основою і висотою h , що дорівнює ординаті деякої точки ξ [a; b] (рис.4).

	y			y=f(x)
	f(ξ)
	f(ξ)
	0
	0	a	ξ	b x
Рис.4. Геометрична інтерпретація теореми про середнє
4. Інтеграл зі змінною верхньою межею
Нехай в інтегралі ∫b	f (x)dx нижня межа a фіксована, а верхня межа b змінюється. Тоді
a

значення інтеграла залежить від b і є функцією від верхньої межі.

Оскільки верхня межа змінюється, то позначимо її через x , а змінною інтегрування нехай

буде t . Отримаємо функцію, що залежить від x , яку позначимо Φ(x)									і назвемо інтегралом зі
змінною верхньою межею
Φ(x) = ∫x	f (t)dt .								(4.1)
a
Ця функція має такі властивості:
Теорема 4.1. Якщо		f (x)	– інтегровна на [a,b], то Φ(x)				є неперервною функцією від x на
цьому проміжку.
Теорема 4.2. Якщо		f (x)	– неперервна функція і Φ(x) = ∫x				f (t)dt , то
						a
′
Φ (x) = f (x) .
˛ Надаючи аргументу x приросту				x , матимемо
	x+ x		x	x+ x
Φ(x + x) = ∫		f (t)dt = ∫ f (t)dt + ∫ f (t)dt .
	a		a	x
Тоді приріст функції Φ(x) запишеться
				x	x+	x	x	x+	x
	ΔΦ = Φ(x + x) −Φ(x) = ∫ f (t)dt +				∫	f (t)dt −∫ f (t)dt =		∫ f (t)dt .
				a	x		a	x

Застосуємо до останнього інтеграла теорему про середнє

x+ x

ΔΦ = ∫f (t)dt = f (ξ) x , де ξ [x; x + x].

Знайдемо границю відношення приросту функції Φ(x) до приросту аргументу x , яка дорівнює похідній функції Φ(x) :

′	ΔΦ		f (ξ) x		= lim f (ξ) .
Φ (x) = lim		= lim
	x			x
x→0		x→0			x→0
Оскільки ξ → x при		x → 0 і		f (x) - неперервна, то
′		= lim f (ξ) = f (x) .
Φ (x) = lim f (ξ)
x→0		ξ→x

Іншими словами теорему (4.2) можна сформулювати так: похідна від інтеграла (4.1) зі змінною верхньою межею x дорівнює значенню підінтегральної функції в точці x .

можна розглядати як первісну

Зауваження. Оскільки Φ (x) = f (x) , то функцію Φ(x) = ∫f (t)dt

′

функції f (x) . З (3.1) випливає, що Φ(a) = 0 , тобто Φ(x) є тією первісною функції f (x) , що

перетворюється в нуль при x = a .

Геометрична інтерпретація теореми 4.2. Інтеграл Φ(x) = ∫x

f (t)dt чисельно дорівнює площі

криволінійної трапеції ABCD .

y=f(x)

f(ξ)

(x)

Ф(x)

x+ x

Рис.5. Геометрична інтерпретація теореми 4.2.

Приріст ΔΦ(x) = Φ(x + x) − Φ(x) = f (ξ)

x (згідно з теоремою про середнє) дорівнює площі

криволінійної трапеції з основою

′

дорівнює довжині відрізка CD .

x ; похідна Φ

(x) = f (x)

5. Обчислення визначених інтегралів. Формула Ньютона-Лейбніца

5.1. Основна формула інтегрального числення

Якщо F(x) – довільна первісна неперевної на [a,b] функції

f (x) , то справедлива формула

∫b

f (x)dx = F (b) − F(a) ,

(5.1)

яка називається формулою Ньютона-Лейбніца.

˛ Нехай F(x) – деяка первісна f (x) . Згідно з теоремою 4.2, функція ∫x

f (t)dt є також

первісною f (x) . Проте дві довільні первісні функції

f (x)

відрізняються між собою на стале

число C * . Отже,

∫x

f (t)dt = F (x) +C * .

Ця рівність перетворюється у тотожність при деякому значенні C * , яке знайдемо, поклавши

x = a :		∫a	f (t)dt = F(a) +C * ,		або 0 = F(a) + C * , звідки C* = −F(a) . Отже,
		a
∫x	f (t)dt = F (x) − F(a) .
a
Вважаючи x = b , отримаємо формулу ∫b						f (t)dt = F (b) − F(a) , або, згідно з властивістю 1
					a
визначеного інтеграла, дістанемо (5.1)
Якщо ввести позначення					F(b) − F(a) = F(x)		b , то формулу (5.1) можна записати у вигляді
Якщо ввести позначення					F(b) − F(a) = F(x)		b , то формулу (5.1) можна записати у вигляді
	∫b			ba .			a
							a
		f (x)dx = F(x)				(5.2)
						(5.2)

	a

Отже, значення визначеного інтеграла виражається різницею двох значень довільної первісної функції – у верхній та нижній межі.

Зауваження. Різниця F (b) − F (a) не залежить від вибору первісної F (x) , оскільки всі первісні відрізняються на сталу величину, яка при відніманні все одно зникає.

Формула Ньютона-Лейбніца дає зручний спосіб обчислення визначеного інтеграла у тому випадку, коли відома первісна підінтегральної функції.

													3	1
Приклад 5.1. За формулою Ньютона-Лейбніца знайти інтеграли: ∫xdx ;														∫ex dx .
													1	0
3	x2	3		9		1			1 x			1
3
а) ∫xdx =											x
		1	=		−		= 4	;	б) ∫e	dx =e		0	=e −1 .
	2		=	2	−	2	= 4	;	б) ∫e	dx =e			=e −1 .
1	2			2		2			0

5.2. Заміна змінної у визначеному інтегралі

За допомогою основної формули інтегрального числення (5.1) формули теорії невизначеного інтеграла перетворюються в аналогічні формули для визначеного інтеграла, які зводять обчислення одного інтеграла до обчислення іншого, більш простого. Це стосується як методу заміни змінної, так і інтегрування частинами.

Теорема 5.1. Нехай в інтегралі ∫b			f (x)dx функція f (x) неперервна на відрізку [a;b]. Введемо
		a
нову змінну t , поклавши x=ϕ( )t. Нехай значенню t =α за формулою				x=ϕ( )t відповідає
значення x = a , а значенню t = β – значення x = b , тобто ϕ(α) = a , ϕ(β) = b . Тоді,
якщо:		неперервно-диференційовна на [α; β];
1) функція ϕ(t)		неперервно-диференційовна на [α; β];
2) складна функція f (ϕ(t)) визначена і неперервна на [α; β], то
b	β
∫f (x)dx = ∫f (ϕ		′		(5.3)
∫f (x)dx = ∫f (ϕ		(t))ϕ (t)dt .		(5.3)
a	α

Зауваження. Зазначимо одну особливість цієї формули. В той час, як при обчисленні невизначеного інтеграла за допомогою заміни змінних, отримавши шукану функцію через змінну t , ми повинні були повертатись до старої змінної x , у визначеному інтегралі у цьому немає необхідності. Якщо вдасться обчислити другий інтеграл у формулі (5.3), то отримаємо деяке число, якому дорівнює перший інтеграл.

e	ln x	dx .
Приклад 5.2. Обчислити: ∫
1	x

x = et ; t = ln x

e	ln x		dx = et dt	1		tt	1	1		3			1
∫		dx =		= ∫			et dt = ∫t		dt =	2	t			=	2	.
								2				2
	x		x =1 при t = 0		e					3			0		3
1				0			0
			x = e при t =1

Приклад 5.3. Обчислити: ∫ 1 − x2 dx .

						0
	Зробимо заміну змінних x =sin t ,								dx = cos tdt		і встановимо нові межі інтегрування: x = 0 при
t = 0 ; x =1 при t = π						. Тоді:
				2
1			π			π			π
1		2	2		2	2	2		2	1 + cos 2t		t		sin 2t	π		π	.
∫	1 − x		dx = ∫	1 −sin		t cos tdt = ∫cos		tdt = ∫			dt = =		+		2	=
∫	1 − x		dx = ∫	1 −sin		t cos tdt = ∫cos		tdt = ∫		2	dt = =	2	+	4	2	=	4
0			0			0			0	2		2		4	0		4
0			0			0			0

Якщо проміжок інтегрування є симетричним відносно початку координат, то для парної функції

інтеграл запишеться ∫a

f (x)dx =2∫a

f (x)dx ,

а для непарної функції – ∫a

f (x)dx =0 .

−a

Приклад 5.4. Обчислити інтеграл

xdx

∫

+1)

−1

xdx

Оскільки функція f (x) =

– непарна, то ∫

= 0 .

+1)

−1

5.3. Формула інтегрування частинами у визначеному інтегралі

[a;b] функції. Тоді

Нехай u(x)

і v(x) – неперервно-диференційовні за змінною x на відрізку

d(uv) =udv +vdu . Інтегруючи цю рівність по проміжку від a до b , матимемо

∫b d (uv) = ∫b udv + ∫b vdu ,

звідки, враховуючи, що ∫b d (uv) =uv

ba , отримаємо

∫b udv = uv

ba −∫b vdu .

(5.4)

Формула (5.4) називається формулою інтегрування частинами у визначеному інтегралі.

Приклад 5.5. обчислити інтеграл

∫2 x cos xdx .

u = x, du = dx

∫x cos xdx =

= x sin x

− ∫sin xdx =

dv = cos xdx, v =sin x

+ cos x

2 =

−1 .

6. Наближене обчислення визначених інтегралів

Нехай треба знайти визначений інтеграл ∫b

f (x)dx , де f (x) – деяка неперервна на [a,b]

функція. У цьому розділі ми вже показали, як знайти такий інтеграл за допомогою первісної у замкнутому вигляді. Цей метод застосовується лише до досить вузького класу функцій, за межами цього класу використовують різні методи наближених обчислень. Найпростішими з них є метод прямокутників, метод трапецій та метод парабол (метод Сімпсона).

При виборі наближених методів обчислення визначеного інтеграла намагаються використати можливості сучасної обчислювальної техніки.

6.1. Метод прямокутників

Поділимо відрізок [a;b] точками a = x0 , x1 , x2 ,..., xn−1 , xn = b на n рівних частин довжиною

x = b −a	і на кожному відрізку [xi−1	; xi ] виберемо середню точку ξi =	xi−1 + xi	( i =1, 2...n )

n		2
(рис.7).

y
					y=f(x)
0	a ξ	x1	x2	xi-1ξ xi	xn-1ξ b	x
		1		i	n
Рис.7. Ілюстрація методу прямокутників

Тоді визначений інтеграл можна обчислити за формулою

b		n			b −a	n		b −a	(f (ξ1 ) +... + f (ξn )),
	f (x)dx ≈		f (ξi )	x =			f (ξi ) =
∫		∑			n	∑
								n
a		i=1				i=1

яка називається формулою прямокутників. Очевидно, що чим більшим буде n , тим меншим буде крок x і права частина даватиме точніше значення інтеграла.

6.2. Метод трапецій

Очевидно, що ми отримаємо точніше значення визначеного інтеграла, якщо криву y = f (x)

наблизимо не ступінчастою лінією, як це було у формулі прямокутників, а ламаною лінією. Тоді площа криволінійної трапеції заміниться сумою площ відповідних прямокутних трапецій (рис.8)

f (x

i−1

) +

f (x

)

f (x

) +

f (x

)

f (x

) +

f (x

)

∫ f (x)dx ≈ ∑

x =

i=1

f (x2 ) + f (x3 ) +...

+ f (x1 ) + f (x2 ) +... + f

де yi = f (xi ) (i = 0, n)

f (x

n−1

) + f (x

)

(x ) + f

)

))=

b −a

+ y

+... + y

n−1

. Зі збільшенням числа n збільшується точність цієї формули.

y					y=f(x)
yn					y=f(x)
yn
yi
yi-1
y0
0	a	x1	xi-1	xi	b x
	Рис.8.	Ілюстрація методу трапецій

6.3. Метод парабол (формула Сімпсона)

Поділимо відрізок [a;b] на 2n однакових частин. Площу криволінійної трапеції, що відповідає першим двом відрізкам [x0 ; x1 ] та [x1; x2 ] і обмеженої кривою y = f (x) , замінимо

1 / 21 2 > Следующая >>>

Соседние файлы в папке 2. Лекції

#
12.02.2016403.31 Кб41Лекції 12-14.pdf
#
12.02.2016370.63 Кб40Лекції 22 - 23.pdf
#
12.02.2016389.41 Кб55Лекції 9-10.pdf
#
12.02.2016436.41 Кб114Лекція 1.pdf
#
12.02.2016377.09 Кб44Лекція 11.pdf
#
12.02.2016379.34 Кб42Лекція 15-16.pdf
#
12.02.2016333.43 Кб41Лекція 17-18.pdf
#
12.02.2016320.45 Кб54Лекція 19.pdf
#
12.02.2016280.94 Кб53Лекція 2.pdf
#
12.02.2016311.55 Кб39Лекція 20.pdf
#
12.02.2016320.03 Кб43Лекція 21.pdf