
Лекції та практичні з МатАналізу / 2. Лекції / Лекція 21
.pdf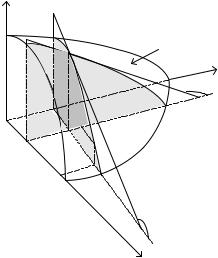
Лекція 21. Частинні похідні. Повний диференціал. Геометричне тлумачення. Застосування. Похідна складеної функції, повна похідна
1.Частинні похідні функції двох змінних
Розглянемо функцію |
|
|
|
|
|
|
z = f (x, y) . |
|
|
|
|
|
(1.1) |
Нехай точка M (x, y) |
належить області визначення функції (1.1) |
M (x, y) D f разом із деяким околом. |
||||
Надамо змінним x та |
y приростів x та |
y відповідно (рис.1). Введемо позначення для частинних приростів |
||||
функції z |
|
y z = f (x, y + y) − f (x, y) . |
||||
x z = f (x + x, y) − f (x, y) , |
||||||
|
z |
|
B |
|
|
|
|
F |
D |
|
z=f(x,y) |
|
|
|
K |
|
M(x,y,z) |
|
||
|
|
|
|
|||
|
|
| |
xz| |
|
|
β y |
|
|
|
|
|
|
|
|
0 |
y |
Q |
|
S |
E |
|
|
|
|
|
|
|
|
x |
|
P(x,y) |
R |
|
|
|
|
|
|
|
|
|
|
|
x+ |
x |
С |
|
|
|
|
|
|
|
|
|
α
A x
Рис.1 Геометрична інтерпретація частинного приросту функції
Означення 1.1. Частинною похідною по змінній x |
функції (1.1) називається скінченна границя (якщо вона |
|||||||||||||
існує) відношення частинного приросту |
x z |
до приросту аргумента x , якщо x → 0 . Позначають |
||||||||||||
|
∂z |
|
≡ lim |
x z |
|
≡ lim |
|
f (x + |
x, y) − f (x, y) |
. |
||||
|
∂x |
x |
|
|
|
|||||||||
|
|
x→0 |
|
x→0 |
|
|
x |
|
|
|
|
|||
Застосовують також наступні позначення: |
|
|
|
|
||||||||||
|
z'x , f x' (x, y), |
∂f (x, y) |
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
Аналогічно частинна похідна за змінною y |
|
|
|
|
||||||||||
|
∂z |
|
≡ lim |
y z |
|
≡ lim |
|
f (x, y + y) − f (x, |
y) |
. |
||||
|
∂y |
|
y |
|
|
|
y |
|
|
|
||||
|
|
y→0 |
|
y→0 |
|
|
|
|
|
|
||||
Використовують також позначення z'y , |
f y' (x, y), |
∂f (x, y) . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
||
Частинні похідні можна розглядати як швидкості зміни функції відносно однієї із змінних (у напрямку відповідної осі координат).
Зауваження. Обчислюючи частинні похідні, використовуємо всі відомі нам формули і правила для знаходження звичайних похідних функції однієї змінної, оскільки фіксуючи одну із змінних (вважаючи її постійною величиною), маємо справу із функцією однієї змінної.
Приклад 1.1. Знайти частинні похідні функцій а) z = ln(x2 + y2 )

|
|
∂z |
|
= |
1 |
|
|
|
∂ |
(x2 + y2 ) = |
|
|
2x |
|
; |
|||||||
|
|
∂x |
|
|
|
|
|
|
|
x2 + y2 |
|
|||||||||||
|
|
|
|
|
x2 + y2 ∂x |
|
|
|
||||||||||||||
|
∂z |
|
= |
|
1 |
|
|
∂ |
(x2 + y2 ) = |
|
|
|
2 y |
|
; |
|||||||
|
∂y |
|
|
|
|
|
|
|
x2 + y2 |
|||||||||||||
|
|
|
|
x2 + y2 ∂y |
|
|
||||||||||||||||
б) z = xy + yx + x −2 y |
|
|
|
|
|
|
|
|||||||||||||||
|
|
∂z |
|
= y x y−1 + yx ln y +1 ; |
|
|
∂z |
= xy ln x + xyx−1 −2 . |
||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
||||
Звернемо увагу на те, що позначення ∂∂xz на відміну від похідної функції однієї змінної не
можна розглядати як відношення двох диференціалів.
Частинні похідні функції довільної кількості змінних визначаються аналогічно.
Нехай дана функція n змінних |
|
|
||||
u = f (x1 , x2 ,…, xn ) . |
(1.2) |
|||||
Тоді частинна похідна функції u |
по змінній xi дорівнює границі частинного приросту функції i u до |
|||||
приросту аргументу |
xi при прямуванні цього приросту до нуля |
|||||
|
∂u |
= lim |
iu ≡ |
|
|
|
|
|
|
|
|||
|
∂x |
xi →0 |
x |
|
|
|
|
i |
|
i |
|
|
|
≡ lim |
f (x1 , x2 ,…, xi + |
xi ,…, xn ) − f (x1 , x2 ,…, xn ) |
. |
|||
|
|
|||||
|
xi →0 |
|
|
x |
||
|
|
|
|
|
i |
|
Приклад 1.2. Знайти частинні похідні функції u = x2 + y2 + xtz3 .
|
∂u |
= 2x +tz3 ; |
∂u |
= 2 y ; |
|
∂u |
= xz3 ; |
∂u |
= 3xtz2 . |
|
|
∂x |
|
∂y |
|
∂t |
∂z |
|
|||
3. Повний приріст і повний диференціал |
|
|
||||||||
Означення 3.1. Повним приростом |
z функції |
|
|
|||||||
z = f (x, y) |
|
|
|
|
|
|
|
(3.1) |
||
в точці M (x, y) |
називається величина, що обчислюється за формулою |
|||||||||
|
z = f (x + |
x, y + |
y) − f (x, y) . |
|
(3.2) |
|||||
Повний приріст - це зміна функції при одночасній зміні обох аргументів. Виведемо формулу для обчислення повного приросту через частинні похідні функції (3.1). Для цього додамо і віднімемо від правої частини рівності (3.2) величину f (x, y + y) . Тоді
z =[ f (x + x, y + y) − f (x, y + y)] +[ f (x, y + y) − f (x, y)] . Застосуємо до обох дужок останньої формули теорему Лагранжа для функції однієї змінної (в кожній із дужок одна із змінних залишається
незмінною). |
|
|
|
|
|
|
Отже, |
|
|
∂f (x, y + y) |
|
|
|
f (x + x, y + y) − f (x, y + y) = |
|
x , |
||||
де x [x, x + x]; |
|
|
∂x |
|
|
|
|
|
|
|
|
||
f (x, y + y) − f (x, y) = |
∂f (x, y) |
|
y , де y [y, y + y]. |
|||
∂y |
||||||
|
|
|
|
|
||
Отже,
z = |
∂f (x, y + y) |
|
|
∂x |
|
Оскільки, згідно з припущенням,
x + ∂f (∂xy, y) y .
частинні похідні неперервні, то

lim |
∂f ( |
x, |
y + |
|
y) = ∂f (x, y) |
, |
||
x→0 |
|
∂x |
|
∂x |
|
|||
y→0 |
|
|
|
|
|
|
|
(3.3) |
|
∂f (x, |
|
) |
|
∂f (x, y) |
|||
lim |
y |
= |
|
|||||
x→0 |
∂y |
|
∂y |
|
||||
y→0 |
|
|
|
|
|
|
|
|
( x, y знаходяться відповідно між x та x + x , y та y + y , тому при x →0, y →0 x та y прямують відповідно до x та y ). Рівності (3.3) можна записати у вигляді
|
|
∂f (x, y + y) |
= ∂f (x, y) |
+α1 , |
|
∂f (x, y) |
= ∂f (x, y) +α2 , |
|
||||||||||||||||
|
|
|
|
∂x |
|
|
|
∂x |
|
|
|
|
|
∂y |
|
∂y |
|
|
|
|||||
де α1 , α2 |
__ нескінченно малі величини, |
тобто прямують до нуля, якщо x →0, y →0 (або |
ρ →0 , де |
|||||||||||||||||||||
ρ = |
x2 + |
|
y 2 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тоді приріст функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
z = |
|
∂f (x, y) |
|
|
x +α1 |
x + |
∂f (x, y) |
|
y +α2 |
y . |
|
|
|
|||||||||
|
|
|
|
∂x |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|||
Означення 3.2. Вираз |
∂f (x, y) |
x + ∂f (x, y) |
|
y називають головною частиною приросту функції двох |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
змінних або лінійною частиною приросту. |
|
|
|
|
|
|
|
|
|||||||||||||||
Означення 3.3. Функція |
z = f (x, y) , повний приріст якої |
z |
в даній точці M (x, y) може бути поданий у |
|||||||||||||||||||||
|
вигляді суми двох доданків: лінійного відносно |
x та |
y |
виразу та нескінченно малої величини вищого |
||||||||||||||||||||
|
порядку відносно ρ , називається диференційовною в даній точці, а лінійна частина приросту |
|||||||||||||||||||||||
|
називається диференціалом цієї функції і позначається dz або df . |
|
||||||||||||||||||||||
Отже, |
|
∂z |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dz = |
x + |
|
y . |
|
|
|
|
|
|
|
|
|
|
|
|
(3.4) |
||||||
|
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Прирости незалежних аргументів |
x |
та |
y |
будемо називати диференціалами незалежних змінних x та |
||||||||||||||||||||
y і позначати відповідно dx , dy . Тоді формула (3.4) набуде вигляду |
|
|||||||||||||||||||||||
|
|
dz = |
∂z |
dx + |
∂z |
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.5) |
||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
або в інших позначеннях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
df = |
|
∂f (x, y) |
dx + |
∂f (x, y) dy . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Іноді |
використовують |
позначення |
|
|
dzx |
= ∂z dx , |
dz y |
= |
∂z |
dy , а самі вирази називають |
частинними |
|||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|||
диференціалами функції z |
двох змінних. |
|
|
|
|
|
|
|
|
|
||||||||||||||
Висновок. Якщо функція z = f (x, y) |
має неперервні частинні похідні в точці (x, y) , то вона диференційовна |
|||||||||||||||||||||||
в цій точці, а її повний диференціал дорівнює сумі добутків частинних похідних цієї функції на диференціали відповідних незалежних змінних.
Приклад 3.1. Знайти частинні похідні та повний диференціал функції Коба-Дугласа
Y = Y0 Kα L1−α , 0 <α <1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂Y |
= Y α Kα−1 |
L1−α = |
α Y Kα |
L1−α = α Y , |
|
||||||||||||||
|
|
|
||||||||||||||||||
|
∂K |
0 |
|
|
|
|
|
|
K |
0 |
|
|
|
K |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂Y |
|
|
|
|
|
α |
−α |
|
1 −α |
|
|
α |
1−α |
|
1 −α |
||||
|
|
= Y |
(1 − |
α) K |
|
L |
= |
|
|
|
Y |
K |
|
L |
= |
|
|
Y. |
||
|
|
|
|
|
|
|
|
|
||||||||||||
|
∂L |
0 |
|
|
|
|
|
|
|
|
L |
0 |
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Зауважимо, що |
|
∂Y |
> 0 та |
|
∂Y |
> 0 . |
|
|
|
|
|
|
|
|||||||
|
∂K |
|
∂L |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Повний диференціал цієї функції

dY = αK YdK + 1 −Lα YdL = Y ( αK dK + 1 −Lα dL) .
Приклад 3.2. Знайти частинні похідні та повний диференціал наступних функцій
а) |
z = ex2 +ey2 |
|
∂z |
|
|
|
|
|
|
||||
|
|
∂z |
= 2xex2 ; |
|
= 2 yey2 ; dz = 2xex2 dx + 2 yey2 dy . |
|
|||||||
|
|
∂x |
|
∂y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
б) |
|
z = min{x, y} . |
|
|
|
|
|
|
|||||
|
Запишемо цю функцію наступним чином: |
|
|
||||||||||
|
z = |
x, |
x ≤ y |
. |
|
|
|
|
|
|
|||
|
|
x > y |
|
|
|
|
|
|
|||||
Тоді |
|
y, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂z |
|
1, x ≤ y |
, |
∂z |
0, x ≤ y |
, |
dx, x ≤ y |
. |
||||
|
|
|
= |
x > y |
|
= |
dz = |
> y |
|||||
|
∂x |
∂y |
|||||||||||
|
|
0, |
|
|
1, x > y |
|
dy, x |
|
|||||
4. Похідні та повний диференціал складної функції
Нехай функція |
|
z = f (x, y) |
(4.1) |
така, що змінні x та y є в свою чергу функціями змінної t . Тобто |
|
z = f (x, y), |
x = x(t) , y = y(t) . |
Тоді z є складною функцією однієї змінної t . Тому похідна функції z по змінній t є звичайною похідною
у сенсі похідної функції однієї змінної |
dz |
. Якщо функції |
x(t), y(t), f (x, y) |
мають неперервні звичайну, чи |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||
частинні похідні за своїми аргументами, то похідна |
dz |
обчислюється за формулою |
|
|
|||||||||||||||||||||||||||||||
dt |
|
|
|||||||||||||||||||||||||||||||||
|
dz |
|
|
|
|
∂z |
|
|
dx |
|
|
|
∂z |
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
|
|
+ |
|
|
. |
|
|
|
|
|
|
|
|
(4.2) |
||||||||||||||||||
|
dt |
|
∂x |
|
|
dt |
∂y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Тоді диференціал функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
dz = |
dz |
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.3) |
||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можна одержати, зробивши підстановку в (4.1) вирази x(t) |
та (y)t. Одержана |
||||||||||||||
Очевидно, що цей результат |
|
||||||||||||||||||||||||||||||||||
функція є функцією однієї змінної |
z = f (x(t), y(t)) . |
|
|
|
|
|
|||||||||||||||||||||||||||||
Приклад 4.1. Обчислити |
dz |
, якщо |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
|
z = 2x−y |
|
|
|
|
|
, |
|
|
x = cost , |
y = sin t . |
|
|
|
|
|
|||||||||||||||||||
|
|
∂z |
|
= 2x−y ln 2 ; |
|
∂z |
= −2x−y ln 2 ; |
|
|
|
|
|
|||||||||||||||||||||||
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dx |
|
= −sin t |
; |
dy |
|
= cost . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тоді згідно з формулою (4.2) одержимо |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
dz |
|
= 2x−y ln 2 (−sin t) − 2x−y ln 2 cos t = −2cos t −sin t ln 2(sin t +cos t) . |
|
|
|
|||||||||||||||||||||||||||||
|
dt |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Формула (4.2) не зазнає істотних змін, якщо |
x і y |
є, своєю чергою, функціями від змінних |
u і |
||||||||||||||||||||||||||||||||
v , тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z = f (x, y) , x = x(u, v) , y = y(u, v) . |
|
|
|
|
|
|||||||||||||||||||||||||||||
Тоді за умови існування неперервних частинних похідних функцій |
f (x, y) , |
x(u, v) , y(u, v) |
за |
||||||||||||||||||||||||||||||||
всіма аргументами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂z |
= |
|
∂f |
|
|
|
∂x |
|
+ |
∂f |
|
|
∂y |
, |
|
|
|
|
|
|
(4.4) |
|
|
|
||||||||||
|
∂u |
|
∂x |
|
|
∂u |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂z |
|
= |
|
∂f |
|
|
|
∂x |
+ |
|
∂f |
|
∂y . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂v |
|
∂x |
|
∂v |
|
∂y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||

Повний диференціал складної функції обчислюється за формулою
|
|
|
|
dz = |
∂z |
|
du + |
∂z |
|
dv . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
∂u |
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Приклад 4.2. Обчислити |
|
∂z |
|
|
|
|
та |
|
∂z |
|
, якщо |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
z = ln(x + 2 y) , |
|
x = u2v , y = |
1 |
u3 |
+u v . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Обчислюємо необхідні частинні похідні. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂z |
= |
|
|
1 |
|
; |
|
|
|
∂z |
= |
|
|
2 |
|
; |
|
∂x |
|
= 2u v ; |
∂x |
|
= u2 |
; |
∂y |
|
= u2 +v |
; |
∂y |
= u . |
||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
x |
+ 2 y |
|
|
|
|
∂y |
|
|
x + 2 y |
|
|
|
∂u |
|
|
|
|
|
|
|
∂v |
|
|
|
|
∂u |
|
|
|
|
|
|
∂v |
|
|||||||||||||
Використавши формули (4.4), одержимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
∂z |
= |
|
|
1 |
|
|
2uv + |
|
2 |
|
|
|
(u2 +v) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂u |
|
x |
+ 2 y |
|
x + 2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
|
|
1 |
|
|
|
|
(2uv + 2u2 + 2v) = 2 |
uv +u2 +v |
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
u2v + |
|
u3 |
+ 2uv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2v + |
2 |
u3 + 2uv |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂z |
= |
|
|
1 |
|
|
|
u2 + |
|
|
2 |
|
|
u = |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
(u2 + 2u) = |
|
|
u + 2 |
|
. |
|
|
|||||||||||||||||||
|
∂v |
|
x |
+ 2 y |
x + 2 y |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
v + |
|
|
|
|
u |
|
+ 2uv |
|
|
|
uv + |
|
|
u |
|
+ 2v |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. Частинні похідні та повний диференціал неявно заданої функції двох змінних
Почнемо розгляд цього питання з неявно заданої функції однієї змінної
F(x, y) =0 , |
(5.1) |
яку у курсі диференціального числення функції однієї змінної ми вже розглядали формально.
Виведемо формулу для знаходження похідної функції (5.1). |
|
Надамо незалежним змінним x та y відповідно приростів x та |
y . Тоді |
F(x + x, y + y) = 0 . |
(5.2) |
Розглянемо різницю |
|
F (x + x, y + y) − F (x, y) =0 . |
|
Ліву частину останньої рівності, що є повним приростом функції двох змінних, можна записати так:
F(x + x, y + y) − F(x, y) = |
∂F |
|
x + |
∂F |
y +α1 x +α2 y , |
|
||||||
∂x |
∂y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
де α1 ,α2 прямують до нуля при |
x →0, |
|
|
y →0 . Оскільки ліва частина останньої рівності |
||||||||
нулеві, то |
|
|
|
дорівнює |
|
|
|
|
||||
∂F |
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
x + |
|
y +α1 |
x +α2 |
y =0 . |
(5.3) |
||||||
|
∂x |
|
∂y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
Поділимо (5.3) на x і обчислимо |
y |
: |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y∂∂F +α1 x = − ∂∂Fx +α2 . y
Спрямуємо x до нуля. В границі отримаємо
∂F
y′x |
def |
dy |
|
∂x |
|
|
|
= |
= − |
. |
(5.4) |
||||
dx |
|
||||||
|
|
|
∂F |
|
|||
|
|
|
|
∂y |
|
||
Розглянемо тепер рівняння вигляду |
|
|
|
|
|||
F(x, y, z) = 0 , |
|
|
|
|
|
(5.5) |
|

яке неявно задає функцію двох змінних.
Знайдемо частинні похідні ∂∂xz , ∂∂yz . Під час обчислення похідної величиною, тому можна використати формулу (5.4), тобто
∂z = − Fx′′ .
∂x Fz
Аналогічно обчислюється похідна ∂∂yz
∂z = − Fy′′ . ∂y Fz
Так само можна обчислити похідні, якщо вважати функцією змінну незалежними аргументами. Отже,
∂y |
|
F |
′ |
|
∂y |
|
F |
′ |
|
∂x |
|
Fy′ |
|
∂x |
|
F |
′ |
|
||
|
= − |
|
x |
, |
|
= − |
|
z |
, |
|
= − |
|
|
, |
|
= − |
|
z |
. |
|
∂x |
Fy ′ |
∂z |
Fy ′ |
∂y |
Fx |
′ |
∂z |
Fx′ |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
∂∂xz вважаємо y постійною
(5.6)
(5.7)
x (або y ), а решта змінних –
(5.8)
Оскільки у неявному заданні функції усі три змінні є рівноправними, то можливий розгляд наступних повних диференціалів
dz = ∂∂xz dx + ∂∂yz dy ,
dy = ∂∂yx dx + ∂∂yz dz , dx = ∂∂yx dy + ∂∂xz dz .
Приклад. 5.1. Обчислити частинні похідні |
∂z |
та |
∂z |
неявно заданої функції xy+z −1 = 0 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
∂y |
|
||
Обчислюємо частинні похідні Fx' , Fy' , Fz' : |
|
|
|
|
|
|||||||||
|
Fx' = ( y + z) xy+z−1, Fy' = xy+z ln x, Fz' = xy+z ln x . |
|
|
|
|
|
||||||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
= − |
( y + z) xy+z −1 |
= − |
y + z |
, |
∂z |
= |
xy+z ln x |
|
=1 . |
|
|
|
|
∂x |
|
xy+z ln x |
|
x ln x |
∂y |
xy+z ln x |
|
|
|
|
|
||
6. Дотична площина та нормаль |
|
|
|
|
|
|
||||||||
Розглянемо поверхню |
S і точку |
M 0 S (див. рис.2). Нехай поверхня S задається рівнянням |
||||||||||||
виду
F(x, y, z) = 0 .
Означення 6.1. Пряма лінія називається дотичною до поверхні в деякій точціM 0 , якщо вона є дотичною до деякої кривої, що лежить на поверхні і проходить через точку M 0 .
Через точку M 0 проходить безліч кривих, що лежать на поверхні S , тому і дотичних до поверхні, що проходять через цю точку буде, взагалі кажучи, безліч.
Означення 6.2. Точка M 0 називається звичайною точкою поверхні S , якщо в цій точці всі три похідні ∂∂Fx , ∂∂Fy , ∂∂Fz існують і неперервні, причому хоча б одна з них відмінна від нуля.
Виявляється всі дотичні прямі до даної поверхні в її звичайній точці M 0 лежать в одній площині.
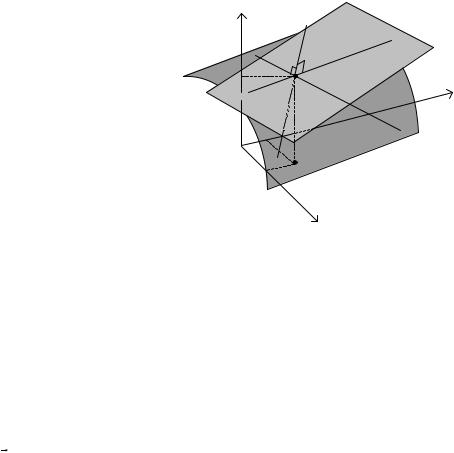
Означення 6.3. Дотичною площиною до поверхні S в точці M 0 називається площина, що містить
всі дотичні до ліній, які проведені на поверхні S через точку M 0 . |
|
|||
6.1. Дотична площина та нормаль до явно заданої поверхні |
|
|||
Нехай поверхня S геометрично зображає явно задану функцію |
|
|||
z = z(x, y) , |
|
|
|
(6.1) |
що має неперервні частинні похідні першого порядку на деякій множині D R2 . |
Тоді рівняння |
|||
дотичної площини до поверхні S в її точці M 0 (x0 , y0 , z0 ), z0 = z(x0 , y0 ) має вигляд |
|
|||
z − z0 =( ∂z ) |M0 |
(x − x0 ) + ( |
∂z |
) |M0 ( y − y0 ) , |
(6.2) |
|
||||
∂x |
|
∂y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
M0(x0,y0,z0) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
0 |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
P0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
|
|
|
|
Рис. 2. Дотична площина та нормальна пряма |
|
|||||||||
де x, y, z - біжучі координати, а |
( ∂z ) |M |
|
, ( |
∂z |
) |M |
|
- значення |
частинних похідних від функції |
|||
|
|
|
|||||||||
|
|
∂x |
|
0 |
|
∂y |
0 |
|
|
|
|
z(x, y) в точці P0 .Точка |
P0 (x0 , y0 ) |
- проекція точки M 0 (x0 , y0 , z0 ) |
на площину XOY (рис. 2 ). |
||||||||
Означення 6.4.Нормаллю до поверхні S |
в точці M 0 (x0 , y0 , z0 ) називається пряма, |
що проходить |
|||||||||
через точку M 0 |
перпендикулярно до дотичної площини, проведеної в точці M 0 |
до поверхніS . |
|||||||||
Рівняння нормалі – це рівняння прямої, що проходить через задану точку перпендикулярно до заданої
площини. |
|
А |
|
саме |
|
|
|
до |
дотичної |
площини, |
вектором нормалі |
|
якої є |
вектор з |
координатами |
||||||||||||||||||||||||||
n( |
∂z |
|
; |
|
∂z |
|
|
|
;−1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
P |
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до явно заданої поверхні S , є таким |
||||||||||||
|
Отже, рівняння нормалі, проведеної в точці M 0 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x − x0 |
= |
|
y − y0 |
= |
z − z0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
||||||||||||
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
( |
) |P |
|
( |
|
∂z |
) |P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6.2. Дотична площина та нормаль до поверхні, заданої неявно |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Нехай поверхня |
|
|
|
S задана рівнянням F(x, y, z) = 0 у неявному вигляді. |
|
|
||||||||||||||||||||||||||||||||||
|
Функція F(x, y, z) = 0 в деякому околі точки M 0 (x0 , y0 , z0 ) S |
|
має неперервні частинні похідні |
||||||||||||||||||||||||||||||||||||||
першого |
|
|
порядку, |
|
|
одночасно |
|
|
не рівні |
нулеві. |
|
|
Тоді |
|
вектор з |
компонентами |
|||||||||||||||||||||||||
((F ' ) |
M0 |
, (F ' |
) |
M0 |
, (F |
' ) |
M0 |
) ≠O . У цьому випадку в точці M |
0 |
(x |
0 |
, y |
0 |
, z |
0 |
) S |
можна провести дотичну |
||||||||||||||||||||||||
|
x |
|
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
площину до поверхніS . Рівняння цієї дотичної площини буде мати вигляд |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
(F ' |
) |
M0 |
(x − x |
0 |
) + (F ' ) |
M0 |
( y − y |
0 |
) + (F ' ) |
M0 |
(z − z |
0 |
) =0 |
|
|
|
|
|
|
|
|
|
(6.4) |
|||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рівняння нормалі відповідно
|
x − x0 |
|
|
|
= |
|
|
|
y − y0 |
|
|
= |
|
|
|
z − z0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.5) |
||||||||||||||||||||||||||||||||||||||
|
(F ' ) |
|
|
|
|
|
|
|
|
|
|
(F |
' ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
M 0 |
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
(F ' ) |
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Приклад 6.1. |
|
|
|
|
Записати рівняння дотичної і нормалі, |
проведених в точці |
M0 до наступних |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поверхонь: |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π ) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
а) |
|
|
z = arctg |
|
, |
|
|
|
M 0 |
(1;1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
б) |
2 |
|
+ 2 |
|
|
|
= 8 , |
|
|
|
M0 (2;2;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
z |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
а) |
|
Функція |
|
|
|
|
|
z = arctg |
y |
|
явно задана, |
|
тому використаємо формули (6.2), |
(6.3), попередньо |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
обчисливши значення частинних похідних в точці P0 (1;1) : |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂z |
|
|
|
|
|
|
|
|
|
− y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− y |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
∂z |
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
1 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= − |
; |
; |
|
|
= |
|
|
|
|
x |
|
|
= |
|
= |
. |
|
||||||||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
∂y |
|
|
|
y2 |
x2 + y2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
1 + x2 |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
1 + x2 |
|
|
P |
|
P |
|
|
|
||||||||||||||||||||||||||||||||
Тоді z − |
π |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
= − |
(x −1) + |
|
( y −1) |
- |
рівняння дотичної площини; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x −1 |
|
|
|
|
|
|
y −1 |
|
|
|
|
|
z − |
π |
|
|
|
|
|
x −1 |
|
|
y −1 |
|
|
|
|
z − |
|
π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
= |
|
|
4 |
|
|
|
|
|
або |
|
= |
|
= |
|
|
|
4 |
|
– |
рівняння нормалі. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
−1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
б) |
|
Рівняння |
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
неявно задає функцію z , тому використаємо формули (6.4), (6.5), де |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
z |
+ 2 |
z |
|
|
= 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
F (x, y, z) = 2 |
z |
|
|
|
|
+ 2 |
|
z |
|
|
−8 . Шукаємо спочатку значення похідних в точці M0 (2;2;1) : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fx' |
|
|
|
|
|
= |
|
ln 2 |
|
|
|
|
x |
|
|
|
|
|
= ln 2 22 = 4 ln 2 ; |
|
Fy' |
|
|
= |
|
ln 2 |
2 |
y |
|
|
= 4 ln 2 ; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
z |
x |
|
|
|
|
|
M 0 |
|
|
x |
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
M 0 |
|
|
z |
|
|
M 0 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Fz' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 2 2 |
|
|
|
= −2 ln 2(4 + 4) =16 ln 2 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= − |
|
ln 2 2 |
z |
− |
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, |
|
рівняння |
|
|
|
|
дотичної |
площини має |
|
вигляд |
4 ln 2(x − 2) + 4 ln 2( y − 2) −16 ln 2(z −1) = 0 , або |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x − 2 + y − 2 − 4z + 4 = 0 |
і, остаточно, x + y − 4z = 0 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рівняння нормалі матиме вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x − 2 |
= |
|
|
|
y −2 |
|
= |
|
|
z −1 |
|
|
|
або |
|
|
|
x − 2 |
= |
y − 2 |
= |
|
z −1 |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4 ln 2 |
|
|
|
|
|
|
4 ln 2 |
|
|
|
|
|
|
−16ln 2 |
|
|
1 |
1 |
|
|
|
|
|
−4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
