Лекції та практичні з МатАналізу / 2. Лекції / Лекція 3

Розглянемо

числову послідовність,

задану загальним

членом

xn =

n +1

.

Зобразимо її члени

точками числової осі (рис. 1).

n

x4

x3

x2

x1

0

1

5

4

3

2

\

4

3

2

Рис.1. Зображення членів послідовності на числовій осі

Легко зауважити, що з ростом n члени послідовності

xn

як завгодно близько наближаються до 1.

При цьому | xn

−1|

з ростом n зменшується:

| x −1|=1, | x

−1|=

1

, | x

−1|=

1

, | x

−1|=

1

,...,| x −1|=

1

,...

1

2

2

3

3

4

4

n

n

Той факт, що число a є границею послідовності xn

записується так: lim xn = a або xn → a при

n→∞

Те, що lim xn = a

геометрично

означає,

що яким би малим не було число ε > 0 всі члени

n→∞

послідовності xn з номерами n > N (ε) будуть знаходитися всередині ε -околу точки a (рис. 2)

a-ε

a

a+ε

x1

x2

x3

xN+1

\

Рис. 2. Графічне зображення збіжної послідовності

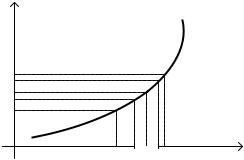
При цьому записують lim f (x) = A . Якщо ж x →∞

так, що x >0 (x < 0) , то кажуть, що число A є

x→∞

)

границею функції f (x) при x →+∞ (x → −∞) і записують lim f (x) = A

lim

f (x) = A

.

x→+∞

(x→−∞

Означення 3. Число

A

називається границею функції f (x)

при x , що прямує до

x0

(або в точці

x0 ), якщо для довільного числа

ε > 0 існує таке число

δ =δ(ε) >0 , що

для всіх x ,

які

задовольняють умову 0 <| x − x0 |<δ , виконується нерівність

| f (x) − A |<ε .

Якщо число

A є границею функції

f (x)

в точці x0 , то пишуть

lim f (x) = A або

f (x) → A

при

x→x 0

x → x0 .

f (x)

Суть означення границі функції

в точці x0 полягає в тому, що для всіх значень x , достатньо

близьких до x0 , значення функції

f (x)

за абсолютною величиною як завгодно мало відрізняються

від числа A .

Геометричний зміст границі функції в точці. Число A

є границею функції f (x) при x → x0 ,

якщо

для

довільного

ε > 0

знайдеться такий проколотий

δ -окіл

точки

x0 , що для всіх

x (x0

−δ; x0 +δ) \ {x0 }

відповідні

ординати точок графіка функції y = f (x)

будуть міститися

в

смузі A −ε < y < A +ε , якою би вузькою ця смуга не була (рис. 3).

Зауважимо,

що в означенні границі функції в точці ніяких умов на спосіб прямування x до x0

не

накладалось. Якщо x → x0 так,

що x > x0 , то така границя називається правосторонньою границею

функції f (x) в точці x0

і позначається

lim

f (x) .

x→x 0 +0

y

A+ε

A

A-ε

x0

x

0

x0-

δ x0+δ

Рис. 3. Графічна інтерпретація означення границі функції в точці

Аналогічно,

lim

f (x) = lim f (x)

– лівостороння границя функції

f (x)

в точці

x0 . Якщо

x→x 0 −0

x→x0

x<x 0

f (x)

x0 = 0 , то

правосторонню і лівосторонню

границі функції

в точці x0

будемо

позначати

lim f (x) і

lim

f (x) відповідно.

x→+0

x→−0

4. Нескінченно малі та нескінченно великі величини

Означення

4.

Функція

α( x)

називається

нескінченно малою

величиною

при

x → x0 , якщо

lim α( x) = 0 .

x→x0

Наприклад, функції y = x2 −9x і y = sin 2x є нескінченно малими при x → 0 .

Функцію f (x) , яка має границю в точці x0 , тобто

lim f ( x) = b , можна представити у вигляді

x→x0

f ( x) = b +α(x), де α( x) – нескінченно мала в точці x0 функція.

Означення 5.

Функція f (x)

називається нескінченно великою величиною при

x → x0 , якщо для

довільного як завгодно

великого числа K > 0 існує таке число δ > 0 , що для всіх x ,

що

задовольняють умову 0 <| x − x0 |<δ , виконується нерівність |

f (x) |> K .

Запис

того,

що функція

f (x) нескінченно велика

при x → x0

наступний:

lim f (x) = ∞

або

f (x) →∞ при x → x0 .

x→x 0

Якщо

lim

f (x) =∞ і при цьому f (x) > 0 (f (x) < 0)

в деякому проколотому околі точки x0 , то

x→x 0

пишуть

lim f (x) = +∞ lim

f ( x) = −∞ .

x→x 0

x→x0

Аналогічно,

lim f (x) =∞, якщо для кожного числа K > 0 існує таке число δ > 0 , що для всіх x ,

x→∞

що задовольняють умову | x |>δ , виконується нерівність | f (x) |> K .

Так, наприклад, функції y = tg x при x →π / 2 і y =

5x − 7 при x →+∞ є нескінченно великими.

f (x) , то існує границя функції

f (x) при x → x0 і вона дорівнює f (x0 ) , тобто lim f (x) = f (x0 ) .

x→x 0

3. Якщо lim f (x) = A і lim g(x) = B

( a – скінченне або дорівнює ∞;+∞;−∞), то:

x→a

x→a

а) lim( f (x) ± g(x)) = lim f (x) ± lim g(x) = A ± B;

x→a

x→a

x→a

б) lim( f (x) g(x)) = lim f (x) lim g(x) = A B;

x→a

x→a

x→a

в) lim(C f (x)) =C lim f (x) =C A, де C = const ;

x→a

x→a

f (x)

lim f (x)

A

г) lim

=

x→a

=

, якщо

B ≠ 0 ;

g(x)

lim g(x)

B

x→a

x→a

lim g ( x)

д)

lim[f (x)]g ( x) =[lim f (x)]x→a

= AB , якщо A > 0 ;

x→a

x→a

е) якщо існує lim h( y) , то lim h(f (x))= lim h(y).

y→A

x→a

y→A

4. Якщо lim f (x) = +∞ і lim g(x) = +∞ , то:

x→a

x→a

а) lim(f (x) + g(x))= +∞ ;

x→a

б)

lim(f (x) g(x))= +∞.

x→a

(A ≠ 0), то:

5. Якщо lim f (x) =∞ і lim g(x) = A

x→a

x→a

а) lim(f (x) g(x))= ∞ ;

x→a

б)

lim(f (x) ± g(x))=∞.

x→a

6. Якщо lim f (x) =∞, то lim

1

=0 .

f (x)

x→a

x→a

7. Якщо lim f (x) =0

і f (x) ≠ 0 в деякому проколотому околі точки x = a , то lim

1

=∞.

f (x)

x→a

x→a

8. Якщо lim f (x) =0

і g(x) обмежена в деякому околі точки x = a , то lim f ( x) g( x) = 0 .

x→a

x→a

а) lim

3x +5

;

б) lim

1

;

в) lim

cos x

.

x −5

x→7

x

→π sin 2x

x→∞

x2

а) Точка

x = 7 разом з деяким околом належить області визначення функції f (x) =

3x +5

.

Тому згідно з твердженням 2

x −5

lim

3x +5

=

3 7 +5

=13 .

x→7

x −5

7 −5

б) Оскільки

lim sin 2x = 0

і для довільного δ <

π

sin 2x ≠ 0 в проколотому δ -околі точки x =π , то

x→π

2

за властивістю 7

lim

1

= ∞ .

sin 2x

x→π

в) Оскільки lim

1

= 0 (твердження 6), а

cos x

≤1 , то за властивістю 8 lim

cos x

= 0 .

x→∞ x2

x→∞ x2