
дискр мат / полнота_бул
.doc
Замкнутость
Определение
Система булевых
функций F
= {![]() }
называется замкнутой относительно
переименования аргументов, если из
того, что n-местная
функция
}
называется замкнутой относительно
переименования аргументов, если из
того, что n-местная
функция
![]()
![]() F,
а
F,
а
![]() - другие
переменные
(среди которых могут быть и совпадающие)
следует, что
- другие
переменные
(среди которых могут быть и совпадающие)
следует, что
![]()
![]() F.
F.
Пример замены переменных
![]() - заменяем
- заменяем
x
на![]() ,
получаем
,
получаем
![]()
Определение
Система булевых
функций F
называется замкнутой относительно
суперпозиции, если из того, что
![]()
![]() F
и
F
и
![]() ,
… ,
,
… ,
![]()
![]() F
следует, что
F
следует, что![]() ,
… ,
,
… ,
![]() =
=
![]() F.
F.
Пример
Функция
![]() ,
соответствующая формуле
,
соответствующая формуле
![]() есть суперпозиция функций
есть суперпозиция функций
![]() =
=
![]() и функций
и функций
![]() ,
,
![]() ,
,
![]() .
.
Определение
Система булевых функций F называется замкнутой, если она содержит тождественную функцию, замкнута относительно переименования аргументов и замкнута относительно суперпозиции.
Пример
Если F
содержит функцию
![]() и
и
![]() и замкнута относительно операций
суперпозиции и переименования переменных,
то F
содержит
и замкнута относительно операций
суперпозиции и переименования переменных,
то F
содержит
![]() ,
поскольку
,
поскольку
![]()
Классы булевых функций
Рассмотрим замкнутые классы булевых функций
Класс функций, сохраняющих 0
Определение
Функция
![]() сохраняет ноль, если
сохраняет ноль, если
![]()
Класс
функций, сохраняющих 0:
![]()
Пример
x&y
Покажем,
что класс
![]() замкнут
замкнут
-
Он содержит тождественную функцию
![]() сохраняет 0.
сохраняет 0.
-
Если
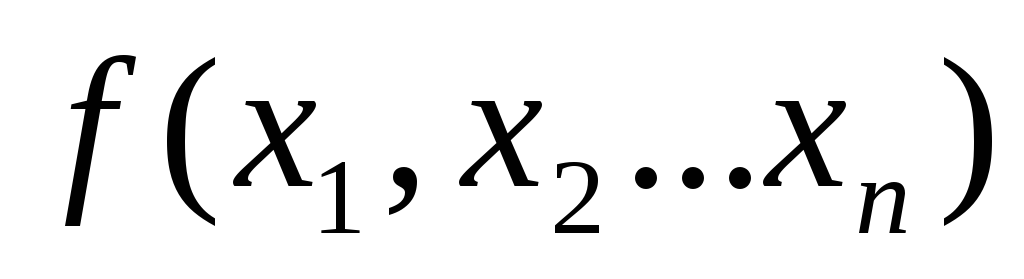 є
є
 и
и
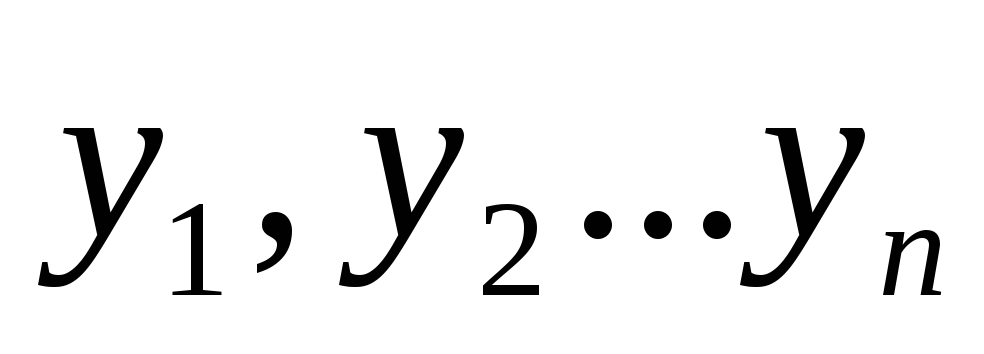 новые переменные, то очевидно, что
новые переменные, то очевидно, что
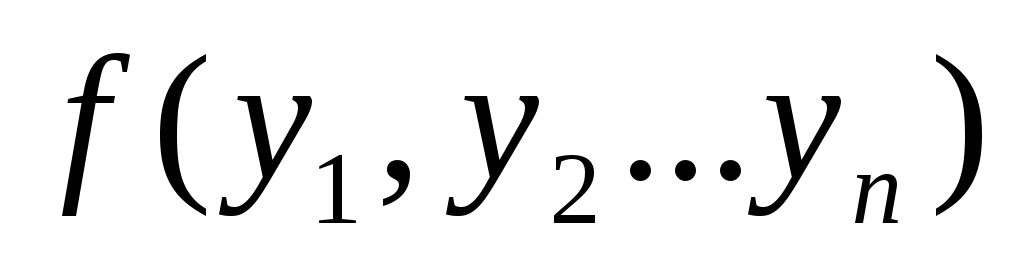 є
є
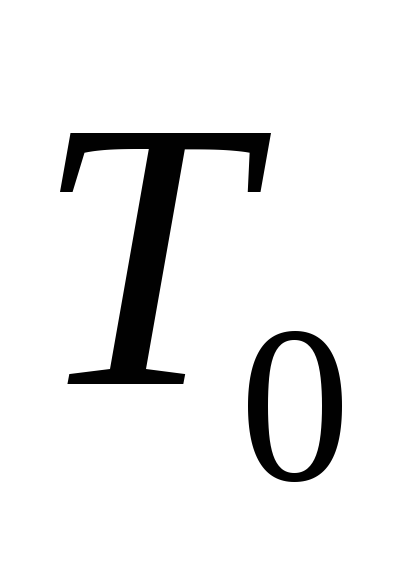
-
Суперпозиция.
Пусть
![]() є
є
![]() и
и
![]() суперпозиция функций
суперпозиция функций
![]() , тогда
, тогда
![]()
![]()
Класс функций, сохраняющих 1
Определение
Функция
![]() сохраняет единицу, если
сохраняет единицу, если
![]()
Класс функций,
сохраняющих 1:
![]()
Пример
![]()
Доказательство
замкнутости аналогично
![]()
Самодвойственные функции
Определение
Функция f самодвойственная, если она равна своей двойственной функции.
![]()
Пример
![]() и
и
![]() .
.
Покажем замкнутость класса самодвойственных функций.
1)
![]() содержит x,
так как x
– самодвойственная функция.
содержит x,
так как x
– самодвойственная функция.
2) Пусть
![]() є
Т* и
є
Т* и
![]() - новый набор переменных. Тогда поскольку
- новый набор переменных. Тогда поскольку
![]() =
=
![]() выполняется
для значений переменных
выполняется
для значений переменных
![]() ,
то оно будет выполняться и для
,
то оно будет выполняться и для
![]() .
Следовательно,
.
Следовательно,
![]() є Т*.
є Т*.
3) Пусть
![]() и
и
![]() .
.
Если выполняется
условие
![]() , (1)
, (1)
то выполняется и следующее условие
![]() (2)
(2)
![]()
![]() =
в силу равенства (2) =
=
в силу равенства (2) =
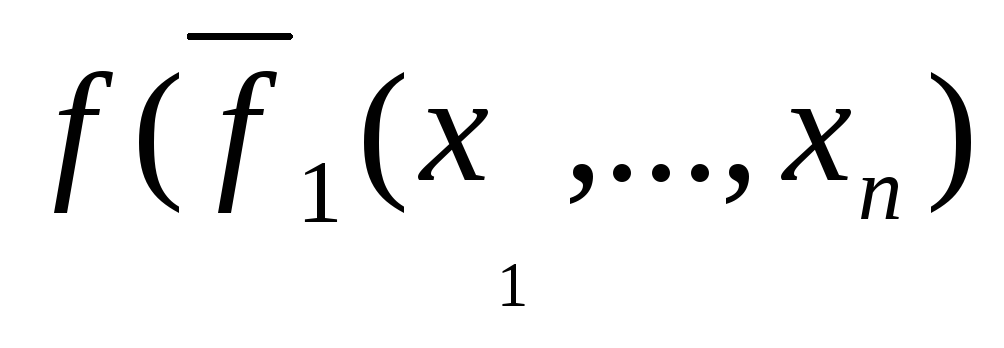 ,…,
,…,![]() .
Следовательно,
.
Следовательно,
![]() *.
*.
Лемма о несамодвойственной функции
Пусть
![]() *,
тогда замыкание класса функций F
= {
*,
тогда замыкание класса функций F
= {![]() ,
-} содержит константы 0 и 1.
,
-} содержит константы 0 и 1.
Доказательство
Так как
![]() *,
то
*,
то
![]()
![]() такие,
что
такие,
что
![]()
Так как функция f
может принимать только два значения,
из этого неравенства следует равенство
![]() .
.
Для удобства
предположим, что
![]() .
Тогда последнее равенство примет вид
.
Тогда последнее равенство примет вид
![]() ; отделяет к-й
аргумент от (к+1)-го.
; отделяет к-й
аргумент от (к+1)-го.
Рассмотрим функцию
![]()
![]() ,
так как получена из функции f
путем переименования аргументов.
,
так как получена из функции f
путем переименования аргументов.
![]()
Следовательно
![]() -
одна из констант 0 или 1, а так как
-
одна из констант 0 или 1, а так как
![]() ,
то обе константы принадлежат классу F.
,
то обе константы принадлежат классу F.
Класс монотонных функций
Определение
Функция
![]() называется
монотонной, если для любых двух векторов
называется
монотонной, если для любых двух векторов
![]() и
и
![]() из условия
из условия
![]() следует, что
следует, что
![]() .
.
![]() тогда и только
тогда когда
тогда и только
тогда когда
![]()
Пример
![]() ,
,
![]() .
.
Д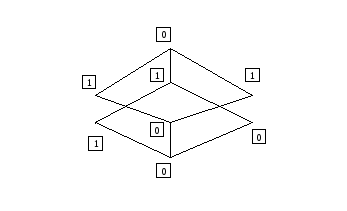 ля
вычисления монотонных функций удобно
построить диаграмму. Рассмотрим ее на
примере функции
ля
вычисления монотонных функций удобно
построить диаграмму. Рассмотрим ее на
примере функции
![]()
(1,1,1)
(1,0,1)
(1,1,0) (0,1,1)
(0,0,1) (0,1,0) (0,0,1)
(0,0,0)
Если в какой-то вершине диаграммы функция принимает значение 1, то всюду выше монотонная функция также должна принимать значение 1.
В нашем случае f(1,1,0)=1, a f (1,1,1)=0, cледовательно функция не монотонная.
Класс монотонных
функций
![]()
Покажем, что класс монотонных функций замкнут
1) Тождественная
функция
![]()
-
Пусть
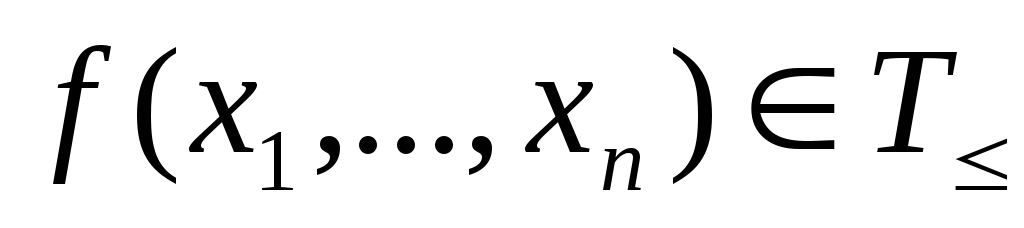 и
и
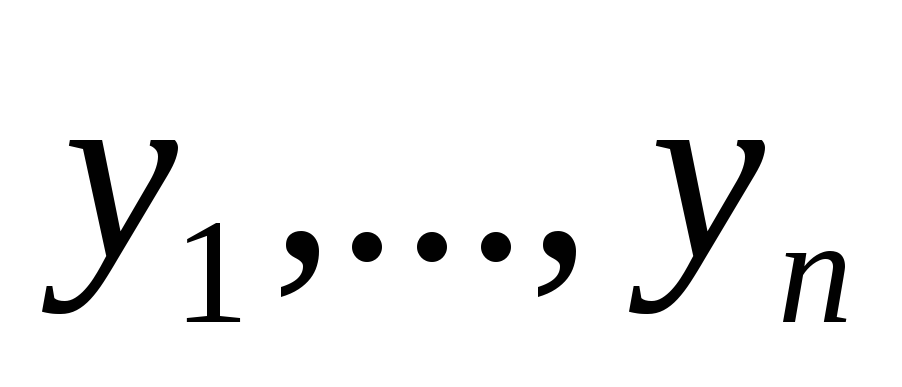 - новые переменные.
- новые переменные.
Возьмем два набора
значений переменных
![]() :
:
![]() и
и
![]() таких,
что
таких,
что
![]() ,
но эти векторы будут значениями и
переменных
,
но эти векторы будут значениями и
переменных
![]() и потому выполняется равенство
и потому выполняется равенство
![]() .
.
-
Пусть
 .
Рассмотрим функцию
.
Рассмотрим функцию

Возьмем два набора
значений переменных
![]() :
:
![]() и
и
![]() ,
таких что
,
таких что
![]() .
.
Обозначим значения
![]()
….
![]()
![]()
….
![]()
В силу монотонности
функций
![]() , i
= 1,…,n
имеем
, i
= 1,…,n
имеем
![]() ,
i
= 1,…,n.
,
i
= 1,…,n.
![]() =
=
=![]() ,
то есть
,
то есть
![]() .
.
Лемма о немонотонной функции
Пусть
![]() .
Тогда замыкание класса
.
Тогда замыкание класса
![]() содержит отрицание.
содержит отрицание.
Доказательство
Так как
![]() то существуют такие наборы
то существуют такие наборы
![]() и
и
![]() ,
что
,
что
![]() ,
а
,
а
![]() .
.
Если
![]() ,
то для любого i
-
,
то для любого i
-
![]() или
или
![]() ,
а
,
а
![]() .
.
![]() ,
следовательно,
,
следовательно,
![]() .
Тогда существует
.
Тогда существует
![]() такой,
что для
такой,
что для
![]()
![]() ,
а
,
а
![]() .
Другими словами J
– это множество индексов, для которых
.
Другими словами J
– это множество индексов, для которых
![]() .
.
Рассмотрим функцию
![]() где
где
![]() ,
если
,
если
![]() и
и
![]() ,
если
,
если
![]() .
.
Тогда
![]() ,
то есть
,
то есть
![]() ,
а
,
а
![]() ,
значит
,
значит
![]() .
.
Полнота булевых функций
Определение
Замыканием класса
булевых функций F
называется класс всех функций, которые
можно получить из F
и тождественной функции с помощью
суперпозиции и переименования переменных.
Обозначение
![]() .
.
Если
![]() ,
то есть замыкание даёт все булевы
функции, то класс функций F
называется полным.
,
то есть замыкание даёт все булевы
функции, то класс функций F
называется полным.
То есть класс F полон, если любую булеву функцию можно получить из F и тождественной функции с полнотою операций суперпозиции и переименование аргументов.
Мы уже знаем один такой класс
Пример
![]()
Утверждение
Если F полный класс булевых функций и любая функция класса F выражается (с полнотою суперпозиции и переименования аргументов) через функции класса G, то G - полный класс.
Действительно
Если любая булева функция выражается через функции класса F, то она будет выражаться и через функции класса G.
Пример
Рассмотрим системы:
1.
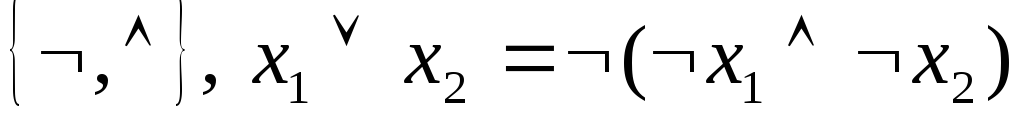
2.![]() ,
, ![]() ,
,
![]() ,
,
![]()
Свойства замыкания
1.![]() -
замыкание класса не уже этого класса.
-
замыкание класса не уже этого класса.
-
[[F]]=[F] - повторное замыкание не расширяет предыдущего замыкания, то есть всякий замкнутый класс замкнут.
3.![]() - вложенность классов сохраняет
вложенность их замыканий.
- вложенность классов сохраняет
вложенность их замыканий.
4.![]() - замыкание объединения не уже объединений
замыканий.
- замыкание объединения не уже объединений
замыканий.
Полином Жегалкина
Как мы уже говорили
система функций
![]() - полная.
- полная.
Представление
булевой функции с использованием
констант 0,1, символов переменных, операций
+ и
![]() называется представлением булевой
функции в виде полинома Жегалкина.
называется представлением булевой
функции в виде полинома Жегалкина.
Общий вид полинома Жегалкина для булевой функции от двух переменных:
![]() ,
,
![]()
для булевой функции от трех переменных:
![]() ,
сі
,
сі
![]() {0,1}
{0,1}
Теорема
Любая булева функция может быть представлена в виде полинома Жегалкина причём в единственным образом.
Доказательство
Любая булева
функция может быть представлена в виде
полинома Жегалкина, поскольку система
функций
![]() - полная.
- полная.
Единственность
вытекает из того, что число всех булевых
функций от n
переменных равно 22![]() и
число различных полиномов от n
переменных равно 22
и
число различных полиномов от n
переменных равно 22![]() .
Число слагаемых в полиноме это число
всех подмножеств множества
.
Число слагаемых в полиноме это число
всех подмножеств множества
![]() ,
а оно равно 2n.
Коэффициенты сi
могут
принимать значение 0 или 1. Поэтому
зафиксировать конечный полином можно
будет 22
,
а оно равно 2n.
Коэффициенты сi
могут
принимать значение 0 или 1. Поэтому
зафиксировать конечный полином можно
будет 22![]() способами.
способами.
При построении полинома используются следующие тождества алгебры логики:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Первым этапом
построения для булевой функции в виде
полинома Жегалкина является приведение
ее к СДНФ. Далее, в полученной формуле,
заменяем дизъюнкцию на сложение по
модулю 2. Если мы воспользуемся формулой
1, то получим
![]() .
Если
.
Если
![]() и
и
![]() конституенты 1, то
конституенты 1, то
![]() .
Обязательно одна из переменных будет
входить в
.
Обязательно одна из переменных будет
входить в
![]() без отрицания, а в
без отрицания, а в
![]() с отрицанием или наоборот.
с отрицанием или наоборот.
Пример
Рассмотрим булеву функцию, представленную СДНФ и построим для нее полином Жегалкина.
![]()
формула 1
=
![]()
формула 3 – убираем отрицания
![]()
формула 2 – раскрываем скобки
![]()
формула 5 и 4
![]() .
.
Второй метод построения полинома Жегалкина – метод неопределенных коэффициентов. Используется общий вид полинома Жегалкина, коэффициенты которого определяются на основе таблицы истинности.
Пример
|
x |
y |
x |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
![]()
![]()
![]()
![]()
![]()
![]()
Найденные
коэффициенты подставим в формулу (1):![]() .
.
Класс линейных функций
Определение
Функция
![]() называется линейной, если она может
быть представлена в виде:
называется линейной, если она может
быть представлена в виде:
![]() ,
,
![]() .
.
Пример
![]()
Класс линейных
функций
![]()
Класс линейных функций замкнут:
Тождественная функция является линейной.
Замкнутость
относительно переименования переменных
очевидна. Суперпозицию доказывается
простой подстановкой. Пусть
![]() ,
,
![]()
![]()
![]()
…
![]()
![]()
Лемма о нелинейной функции
Пусть
![]()
![]() TL
тогда
замыкание класса
TL
тогда
замыкание класса
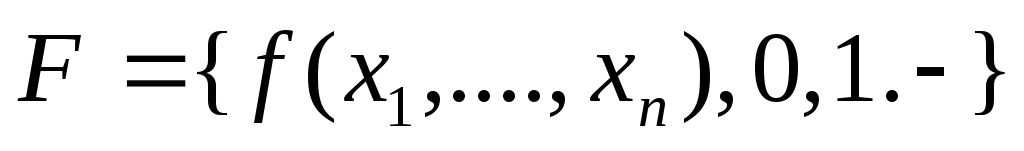 содержит
коньюнкцию.
содержит
коньюнкцию.
Доказательство
Любая функция
может быть задана полиномом Жегалкина.
Так как f![]() TL
, то существует хотя бы одно слагаемое,
которое содержит конъюнкцию по крайне
мере двух переменных. Для определенности
пусть это будут x1
и x2.
Тогда все слагаемые можно разделить на
4 группы:
TL
, то существует хотя бы одно слагаемое,
которое содержит конъюнкцию по крайне
мере двух переменных. Для определенности
пусть это будут x1
и x2.
Тогда все слагаемые можно разделить на
4 группы:
- содержащие x1![]() x2
;
x2
;
- содержащие x1;
- содержащие x2;
- не содержащие x1 и x1.
В первой группе
вынесем за скобки x1![]() x2
, во второй
- x1,
в третьей - x2
.
x2
, во второй
- x1,
в третьей - x2
.
В результате получим:
![]() .
.
Причём
![]() .
.
Следовательно,
существуют такие значения переменных
![]() -
-
![]() ,
что
,
что
![]() .
.
Пусть
![]()
![]()
![]() ,
b,c,d
,
b,c,d
![]() {0,1}э
{0,1}э
Рассмотрим функции:
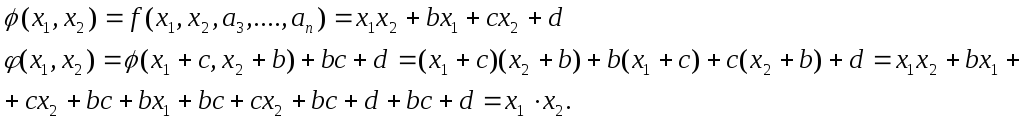
Теорема Поста
Класс булевых функций F полон тогда и только тогда, когда он содержит хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну не монотонную функцию, хотя бы одну нелинейную функцию. При этом функции не обязательно должны быть различны.
Необходимость
Необходимость
будем доказывать от противного. Пусть
![]() и
и
![]() или
или
![]() ,
или
,
или
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
Если
.
Если
![]() один из пяти классов, то
один из пяти классов, то
![]() .
.
![]() ,
поскольку любой из классов является
замкнутым. По свойствам замыкания имеем:
,
поскольку любой из классов является
замкнутым. По свойствам замыкания имеем:
![]() .
Тогда
.
Тогда
![]() ,
но не все булевы функции включаются в
один из классов. Для подтверждения
рассмотрим таблицу:
,
но не все булевы функции включаются в
один из классов. Для подтверждения
рассмотрим таблицу:
|
функция |
|
|
|
|
|
|
0 |
+ |
- |
- |
+ |
+ |
|
1 |
- |
+ |
- |
+ |
+ |
|
|
- |
- |
+ |
- |
+ |
|
|
+ |
+ |
- |
+ |
- |
Для каждого класса существует булева функция, которая ему не принадлежит.
Достаточность
Пусть F
содержит функцию
![]() .
Причем не обязательно, чтобы они все
были разные. Так как
.
Причем не обязательно, чтобы они все
были разные. Так как
![]() ,
то
,
то
![]() .
Относительно значения
.
Относительно значения
![]() рассмотрим два случая.
рассмотрим два случая.
