дискр мат / Функции_алгебры_логики

7

Функции алгебры логики (булевы функции)

Теория булевых алгебр берет свое начало от классического сочинения Джорджа Буля "Исследование законов мысли, на которых основаны математические теории логики и теории вероятностей", изданного в 1854 году. Цель и задачи этой книги автор сформулировал так: "В предлагаемом вниманию читателей трактате мы намереваемся исследовать фундаментальные законы тех операций, которые совершает разум в процессе рассуждений, дабы выразить их в символическом языке исчисления и на этой основе построить науку логики и ее метод". Следуя такой установке, Дж. Буль провел по существу алгебраизацию той логической системы, которая лежит в основе классических математических рассуждений. Таким образом, возникла алгебраическая структура, именуемая ныне алгеброй Буля или булевой алгеброй.

Функция называется булевой или логической, если она принимает только два значения 0 и 1. Каждый из ее аргументов тоже может принимать только два значения 0 и 1. То есть булева функция – это всюду определенная функция, которая задает отображение:

.

Число всевозможных значений наборов для функций от n переменных равно . Число же всех булевых функций равно .

Одним из самых распространенных способов задания булевой функции - это табличный способ.

Строим таблицу из (n+1) столбцов и строк. В n столбцах значения аргументов, в (n+1) столбце значение функции на этом наборе аргументов.

Кроме того, задать булеву функцию можно, перечислив наборы аргументов, на которых функция принимает 0, или, перечислив наборы аргументов, на которых функция принимает 1.

Рассмотрим булевы функции от одного аргумента, f(x):

x	Константа 0	Константа 1	x
0	0	1	0	1
1	0	1	1	0

Рассмотрим булевы функции от двух аргументов, f(x,y):

		конъюнк-ция	дизъюнк-ция	имплика- ция	эквива- лентность	сложение	штрих Шеффера	стрелка пирса
x	y						|
0	0	0	0	1	1	0	1	1
0	1	0	1	1	0	1	1	0
1	0	0	1	0	0	1	1	0
1	1	1	1	1	1	0	0	0

Как мы видим из таблицы истинности:

.

Определение

Булева функция существенно зависит от переменной , если существует такой набор значений аргументов , что

. В этом случае переменная называется существенной, иначе она называется несущественной или фиктивной.

Пример

				Функция существенно зависит от переменных и , - фиктивная переменная. Поэтому для задания функции достаточно задать значения только переменных , . 0 0 0 0 1 1 1 0 1 1 1 0
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Определение

Две булевых функции называются равными, если одну из них можно получить из другой путем удаления фиктивных переменных.

Пример

и вовсе не имеют существенных переменных.

Введем понятие формулы индуктивным способом.

Определение

1. любая логическая переменная – формула;

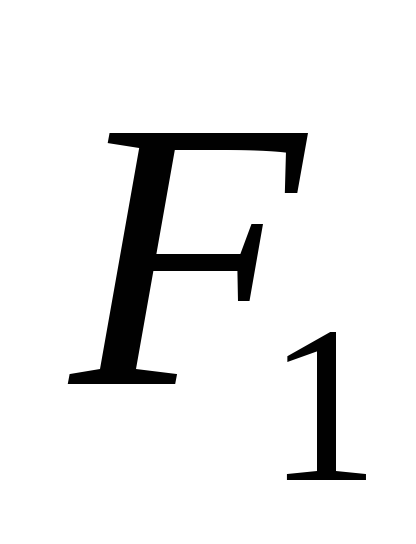2. если и 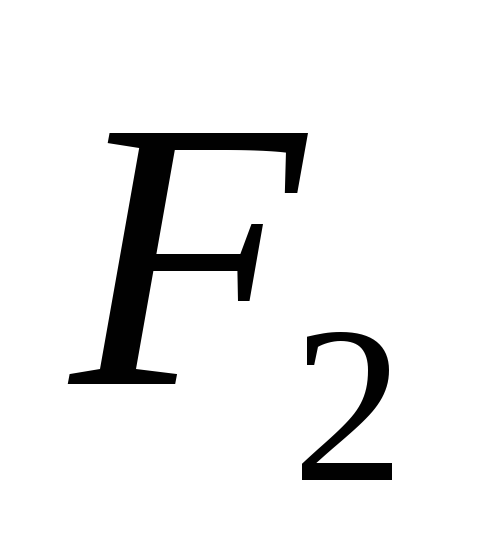- формулы, то 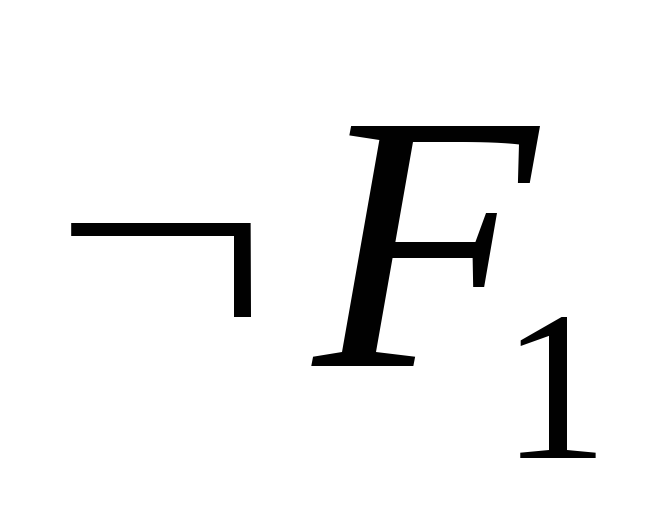, , 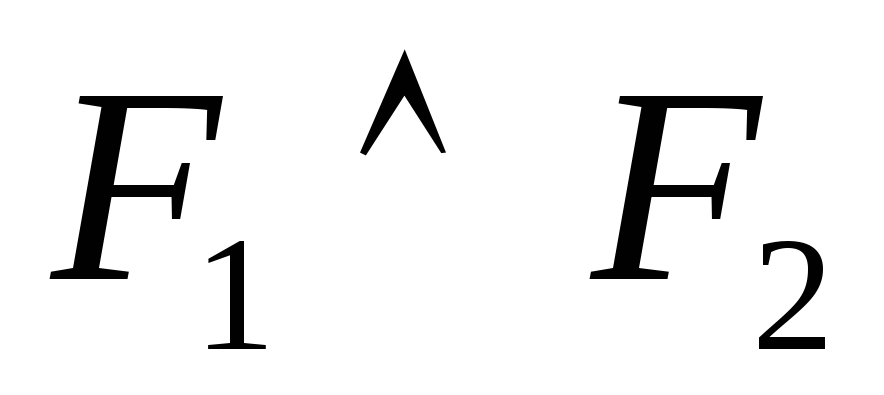, , 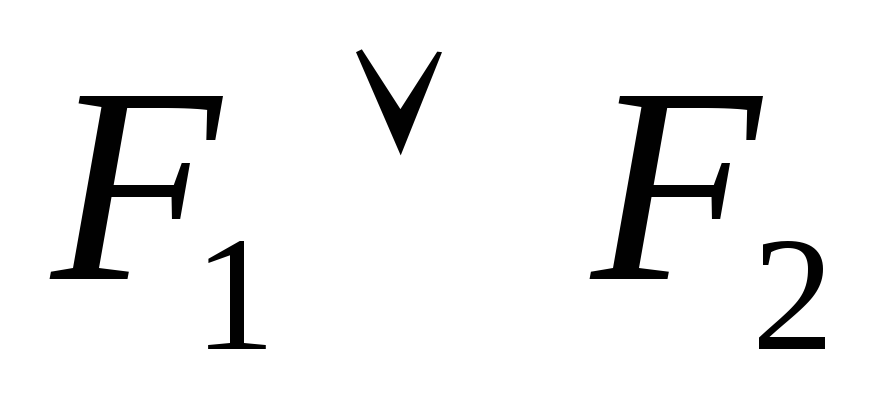, , , 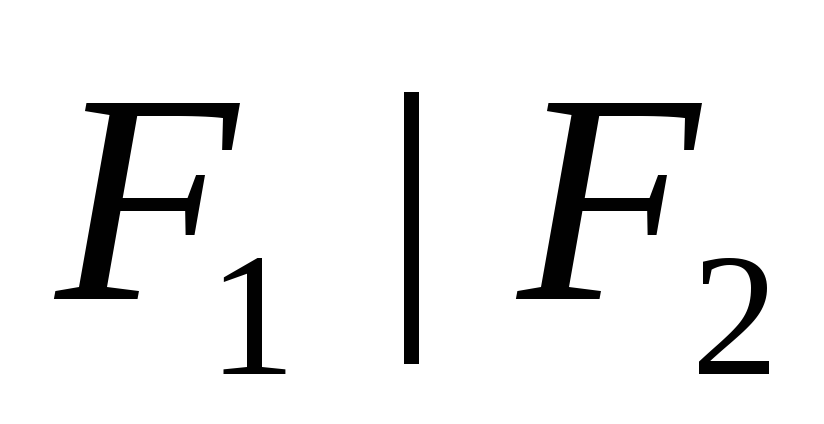являются формулами.

Никаких других формул нет.

Пример

1)

2)

3)

4)

1 и 2 являются формулами булевой алгебры, 3 и 4 – нет.

Каждая формула определяет или реализует некоторую булеву функцию. Одна и та же булева функция может быть реализована несколькими формулами. Но одна формула не может определять несколько булевых функций.

Определение

Две формулы эквивалентны, если соответствующие им функции равны.

Простейший способ установления эквивалентности формул – построение таблицы истинности.

Тождества алгебры логики

Алгебра логики и алгебра множеств являются изоморфными алгебраическими системами, поэтому все тождества алгебры множеств справедливы для алгебры логики:

алгебра логики

А

алгебра множеств

В=

функция, устанавливающая взаимнооднозначное соответствие между алгеброй множеств и алгеброй логики:

.

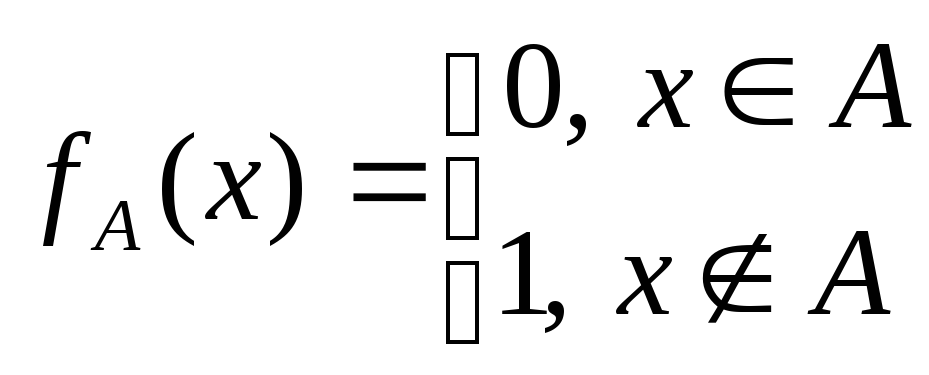
То есть в алгебре логики мы будем иметь все те же тождества, что и в алгебре множеств, но вместо операции у нас будет операция , вместо операции - операция , вместо операции дополнения – операция отрицания, вместо множеств – булевы переменные.

1. коммутативность

;

2. ассоциативность

;

3. идемпотентность

;

4. дистрибутивность

;

5. поглощения

;

6. закон дойного отрицания

7. законы Моргана

;

8. законы дополнения

;

9. законы нуля и единицы

;

;

10)раскрытие импликации и эквивалентности

При составлении сложных формул возникает вопрос порядка выполнения операций. Если есть скобки, то порядок выполнения понятен. Если же скобок нет, то порядок выполнения операций определяется отношением быть более сильным, быть равносильным. Зададим этот порядок:

1)

2)

3)

4)

5) .

Пример

Таблицы истинности для булевой функции представленной формулой

x	y	z
0	0	0	1	1	1
0	0	1	1	1	1
0	1	0	1	1	1
0	1	1	1	1	1
1	0	0	0	1	0
1	0	1	0	1	0
1	1	0	1	0	0
1	1	1	1	0	0

Здесь переменная z – фиктивная.

Определение

Формула называется выполнимой, если существует такой набор переменных, при которых формула принимает значение 1.

Формула называется опровержимой, если существует такой набор переменных, при которых формула принимает значение 0.

Определение

Формула называется тождественно истинной или тавтологией, если эта формула принимает значение 1 на всех наборах переменных, то есть функция является константой 1.

Определение

Формула называется тождественно ложной или противоречием, если эта формула принимает значение 0 на всех наборах переменных, то есть функция является константой 0.

Пример

0	1	0
1	1	0