3.2. Алгоритмы нахождения оптимального пути

Путь из начальной вершины x_Н к конечной вершине x_К - последовательность дуг, начинающаяся в вершине x_НХ, заканчивающаяся в вершине x_КХ, и такая, что конец очередной дуги является началом следующей (i номер пути): (x_Н , x_i1)( x_i1, x_i2)…(x_il-1, x_il)( x_il, x_К).

Элементарный путь – путь, в котором вершины не повторяются.

Простой путь – путь, в котором дуги не повторяются.

Маршрут - последовательность рёбер, составляющих, как и путь, цепочку.

Длина пути взвешенного графа определяется как сумма весов его дуг. Если граф не взвешен, то можно считать веса всех дуг равными 1, и

тогда длина пути - это количество дуг, составляющих путь.

Кратчайшим путем между выделенной парой вершин x_Н и x_К называется путь, имеющий наименьшую длину среди всех возможных путей между этими вершинами.

При построении длиннейшего пути рассматриваются элементарные или простые длиннейшие пути, длиннейшие пути с заданным числом выполненных циклов. Длиннейший путь между x_Н и x_К - путь, имеющий наибольшую длину среди всех возможных путей между этими вершинами.

Волновой алгоритм построения кратчайшего пути для взвешенного графа

Алгоритм называется волновым, так как от рассматриваемой вершины исходит виртуальная волна, которая захватывает смежные с ней вершины.

1. Вершина x_Н получает вес V_Н=0, её номер вводится в массив М номеров вершин, изменивших вес. Остальные вершины x_i получают вес V_i= и их номера не попадают в массив M.

2. Если массив М пуст, то выполняется п. 3, иначе выбирается с исключением из него очередная вершина x_i и пересчитываются веса вершин, принадлежащих исходу E(x_i) вершины x_i: x_iX  V_j=min(V_j, V_i+ l_ij)). Если вес V_i уменьшается, то номер j включается с приведением подобных в М. Снова выполняется п. 2.

3. Если вес V_K=, то делается вывод, что пути из вершины x_н к вершине x_K нет, иначе переход к п. 4.

4. Выполняется процедура выделения дуг, которая заключается в следующем. Выделяем текущую вершину x_i, начиная с конечной, и записываем множество всех вершин, смежных с текущей: E^-1(x_i)={x_j,x_m…}; здесь номера вершин упорядочены по возрастанию. Затем последовательно для каждой вершины из множества E^-1(x_i) определяем вес дуги как разность весов вершин, текущей x_i и рассматриваемой x_j. Если V_i-V_j=l_ij, где l_ij- вес дуги, а V_i, V_j – веса вершин, вычисленные на первом проходе (окончательные значения!), то эта дуга является фрагментом одного из кратчайших путей. Далее x_j полагаем текущей вершиной и переходим на начало этой процедуры. Процедура заканчивается при достижении начальной вершины.

Отметим, что в волновом алгоритме для невзвешенного графа разность весов вершин x_j и x_i должна быть равна 1.

5. После выделения дуг строятся кратчайшие пути, длины которых равны V_k.

Обратите внимание на то, что алгоритм выполняется в 3 прохода. На 1-м проходе (это п. 2 словесного описания алгоритма – СОА) вычисляются и пересчитываются веса всех вершин, включая конечную (x_K=x₆). На 2-м проходе (это п. 4 СОА) выявляютя «претенденты» на кратчайший путь, т.е. дуги, которые могут составить этот путь (эти пути, поскольку их может оказаться несколько с одинаковым весом). На 3-м проходе (это п. 5 СОА) из дуг-претендентов составляются конкретные кратчайшие пути. Задача составления пути из дуг-претендентов является переборной. Здесь важно учесть все возможные варианты перебора.

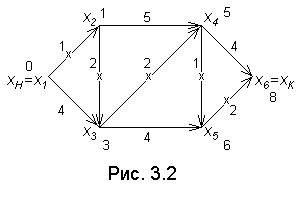
Пример 3.2. Найти кратчайший путь во взвешенном графе (рис.3.2).

Кратко запишем процесс решения задачи (* отмечается дуга, являющаяся претендентом на включение в кратчайший путь)

1. V_Н =V₁=0, V₂ =V₃ =…=V₆ =V_k = , М ={1}.

2. M, i=1, M=, E(x₁)={x₂, x₃}; V₂=min(, 0+1)=1; M={2}.

V₃=min(, 0+4)=4; M={2, 3}.

2. M, i=2, M={3}, E(x₂)={x₃, x₄}; V₃=min(4, 1+2)=3; M={3}.

V₄=min(, 1+5)=6; M={3, 4}.

2. M, i=3, M={4}, E(x₃)={x₄, x₅}; V₄=min(6, 3+2)=5; M={4}.

V₅=min(, 3+4)=7; M={4, 5}.

2. M, i=4, M={5}, E(x₄)={x₅, x₆};

V₅=min(7, 5+1)=6; M={5}.

V₆=min(, 5+4)=9; M={5, 6}.

2. M, i=5, M={6}, E(x₅)={x₆};

V₆=min(9, 6+2)=8; M={6}.

2. M, i=6, M=, E(x₅)=;

3. V_К, переход к п.4.

4. E^1(x₆)={x₄, x₅}; V₆ V₅ = 2, l_5,6 = 2*; V₆ V₄ = 3, l_4,6 = 4.

E^1(x₅)={x₃, x₄}; V₅ V₄ = 1, l_4,5= 1*; V₅ V₃ = 3, l_5,3 = 4.

E^1(x₄)={x₂, x₃}; V₄ V₃= 2, l_3,4 = 2*; V₄ V₂ = 4, l_2,4 = 5.

E^1(x₃)={x₁, x₂}; V₃ V₂= 2, l_2,3 = 2*; V₃ V₁ = 3, l_1,3 = 4.

E^1(x₂)={x₁}; V₂ V₁ = 1, l_1,2 = 1*;

Процесс решения на 1-ом проходе алгоритма можно оформить в виде таблицы (табл. 3.3).

На обратном проходе выделяем претендентов. Из них на 3-м проходе строим путь длиной 8. Кратчайший путь (x_Н,x_К) включает в себя дуги (x_Н=x₁, x₂), (x₁, x₂), (x₂, x₃), (x₃, x₄), (x₄, x₅), (x₅, x₆= x_К).

Таблица 3.3

X1	X2	X3	X4	X5	X6	M
0						1
0	1	4				2, 3
0	1	3	6			3, 4
0	1	3	5	7		4, 5
0	1	3	5	6	9	5, 6
0	1	3	5	6	8	6
0	1	3	5	6	8	