4.4. Определение реакции автомата на входное слово

Пример 4.5. Определить реакцию автомата на входное слово (последовательность входных символов составляет входное слово; аналогично  для выходного слова)

Пусть на вход автомата Мили А_А и эквивалентного ему автомата Мура А_В из примера 4.3 поступает входное слово . Рассмотрим реакцию автоматов на входное слово.

Для автомата Мили имеем: ;, т.е. под действием символа х₁ автомат переходит в состояние с выходом у₁; при следующем символе получим:;и т. д. В результате получим последовательность состояний и выходное слово:

входное слово 		= k *
cостояния S		= k+1
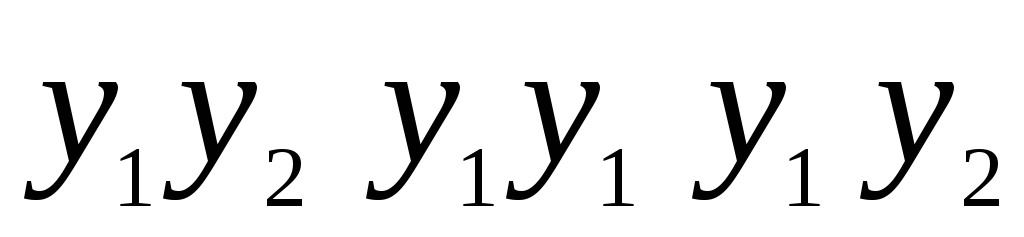
выходное слово 		= k

Для автомата Мура А_В имеем: при вхождении символа х₁ автомат находился в состоянии с выходом,;. Далее поступает следующий символ х₁ в состоянии с выходоми т.д. Последовательность входных и выходных символов, а также символов состояний выглядит аналогично представленным выше для автомата Мили:

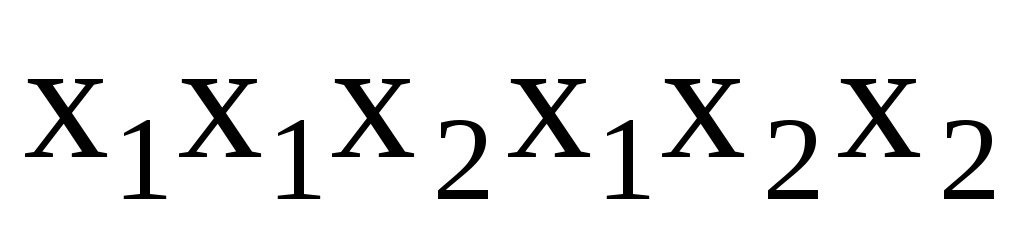
входное слово 		= k
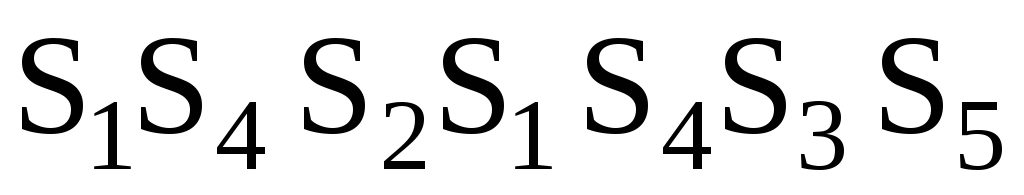
cостояния S		= k+1
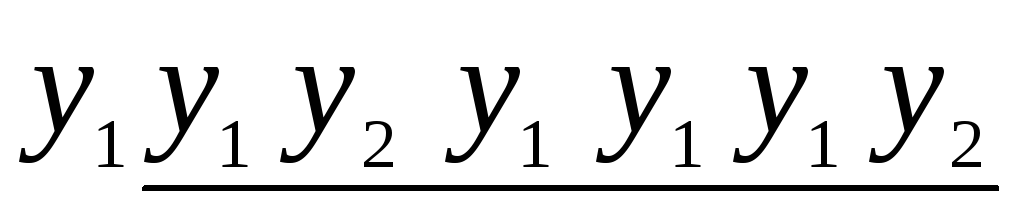
выходное слово 		= k+1

Видно, что реакция автоматов А_А и А_В на входное слово совпадают с точностью до сдвига на один такт; это получилось потому, что реакция автомата Мура на входную букву наступает в следующем такте. Так будет и в общем случае, если автоматы эквивалентны и разных типов. Проверка этого утверждения предоставляется студентам.

4.5. Задания для самостоятельной работы

1. Преобразовать заданный автомат Мили в автомат Мура, а затем последний - в автомат Мили (в табличном и графическом виде).

2. Для всех трёх автоматов из п. 1 определить реакцию на входное слово . Сравнить реакции автоматов и определить, являются ли они эквивалентными

5. Машины тьюринга

5.1. Общие положения

Машина Тьюринга  это конечный автомат, снабжённый бесконечной лентой и читающей/записывающей головкой (просто головкой). Как и автомат, машина Тьюринга (МТ) описывается пятеркой (X, Y, Q, , ). Здесь:

X={x₀, x₁, x₂, … , x_n}  входной алфавит, содержащий пустую букву x₀;

Y={y₀, y₁, y₂,… ,y_n}  выходной алфавит;

Q={q₀, q₁, q₂, …, q_m}  множество внутренних состояний, причем q₀  СТОП-состояние (в этом состоянии МТ не работает);

: QX Q  функция переходов в следующее состояние;

: QX Y  функция выходов.

В свою очередь, Y=XU, где U={R, L, S}  команда на перемещение головки: R  сдвинуться вправо, L  влево, S  стоять на месте.

Задавая МТ [5], вместо двух функций можно пользоваться одной (совме-щающей работу входа и выхода): : QX  QXU, сопоставляющей каждой паре (q_i, x_j) выходную тройку (q_k, u, x_l), uU. Функция  полностью описывает работу МТ и называется логической функцией машины Тьюринга. Таблица этой функции называется функциональной схемой, или программой машины Тьюринга. На каждом такте работы МТ головка обозревает в некоторой ячейке символ x_j, а сама МТ находится в некотором состоянии q_i, что описывается входной парой (q_i, x_j). В зависимости от входной пары МТ выполняет команду (q_k, u, x_l), uU, т.е. записывает в обозреваемую ячейку символ x_l, передвигает головку в зависимости от значения u и переходит в новое состояние q_k. Если на некотором этапе работы МТ переходит в СТОП-состояние, то дальнейших изменений в машине не происходит  машина останавливается.

Последовательность входных символов, записанных в ячейках ленты, будем называть входным словом. Совокупность на ленте слова и состояния МТ для обозреваемой в данный момент ячейки ленты называется конфигурацией в МТ. Конфигурация указывает входную пару и определяет дальнейшую работу МТ. Если из некоторой начальной конфигурации через некоторое число тактов МТ приходит к СТОП-состоянию, то будем говорить, что МТ применима к входному слову; последовательность символов на ленте в момент остановки будем называть результатом преобразования входного слова МТ при данной начальной конфигурации, или просто выходным словом. Если же СТОП-состояние МТ не наступает, то будем говорить, что МТ не применима к входному слову при данной конфигурации.

Поскольку МТ преобразует допустимые входные слова в некотором алфавите в выходные слова в том же алфавите, то с математической точки зрения МТ  это просто определённый алгоритм для преобразования машинных слов. Тем самым при помощи машины Тьюринга уточняется интуитивное понятие алгоритма.

Пример 5.1. МТ А, описываемая пятеркой (X, Y, A, , ), задана своей функциональной схемой (табл. 5.1) и имеет следующие алфавиты^:

Таблица 5.1

X={0, 1}; Y={y1, y2, y3}; A={A0, A1, A2}; y1=(0, R); y2=(1, R); y3=(1, L). А	0	1
А1	0RA2	0RA2
А2	1RA1	1LA0

Рассмотрим два входных слова: ₁=010110 и ₂=00000, и их преобразование машиной Тьюринга (подчеркнутая буква означает, что она обозревается головкой). Соответствующие конфигурации представлены в табл. 5.2. Видно, что МТ А применима к первому входному слову при конфигурации 1 и не применима к пустой ленте (конфигурация 2).

Таблица 5.2

Такт	Состояние	Слово на ленте	Такт	Состояние	Слово на ленте
0	А1	…010110…	0	А1	…00000…
1	А2	…000110…	1	А2	…00000…
2	А1	…001110…	2	А1	…01000…
3	А2	…001010…	3	А2	…01000…
4	А0	…001010…	4	А1	…01010…

Условимся кодировать натуральные числа (с нулём) на ленте МТ, в алфавит которой входят буквы «0» (ноль) и «1» (единица), следующим образом: 01, n111…1 (n+1 единица).

Г

(L) n+1 (R)

… 0111…1 … ,

q_i

оворят, что МТ стандартно воспринимает натуральное числоn в состоянии q_i, если на её ленте имеется конфигурация:

г

(L) n₁+1 n₂+1 n_m+1 (R)

… 011…1011…10…011…10 … .

q_i

де (L) - левая зона (без ограничений), (R) - правая зона (обязательно пустая), читающая головка находится под крайней левой единицей. Аналогично МТ стандартно воспринимает набор (n₁, n₂, …, n_m) в состоянии q_i, если на ленте имеется конфигурация:

МТ М вычисляет функцию y=f(x₁, …, x_n), если выполнены следующие условия:

1. М применима к каждому набору (₁, …, _n), на котором y=f(x₁, …, x_n), определена, и если f(₁, …, _n)=y₀, то М, стандартно воспринимающая набор (₁, …, _n) в начальном состоянии, через конечное число тактов приходит в СТОП-состояние, имея на ленте число y₀.

2. М не применима к наборам, на которых функция f(x₁, …, x_n) не определена.

Функция называется вычислимой по Тьюрингу, если существует вычисляющая её МТ. Вычислимость по Тьюрингу является точным понятием.

Пример 5.2. Функция f(x)=x+1 вычислима по Тьюрингу, так как существует МТ В, которая вычисляет её. Функциональная схема МТ В приведена в табл. 5.3.

Пусть x=n-1 (на ленте записано n+1 единиц) и головка находится у левой границы числа. После n тактов машина передвинет головку к первому справа,

Таблица 5.3

В	0	1
В1	1SB0	1RB1

0, оставаясь в состоянии B₁; на следующем такте машина заменит 0 на 1 и остановится, не передвигая головку.