Алгоритм построения произвольного остова
Рассмотрим словесное описание алгоритма:
1. Для каждой компоненты i графа выполняем пункты 2 и 3.
2. Строим частичный подграф, содержащий все ni вершин i-й компоненты и не содержащий ребер (0- граф).
3. Если в текущий частичный граф включены уже ni-1 ребер, то остов для компоненты i построен, иначе выбираем очередное ребро компоненты и пытаемся его включить в текущий граф.
Если в текущем графе это не приводит к образованию цикла, то включаем ребро, иначе - не включаем. Ребро считаем рассмотренным. Выполняем п. 3.
Пример 3.10.
Рис. 3.10
Так как цикл не образовался, то все рёбра с номерами 1, 2, 3, 4 включены в остов. Проверяем по (3.3): m=4, n=5 и 4=5-1.
Алгоритм построения минимального остова
Для взвешенного графа остов с наименьшей суммой весов для вошедших в него рёбер называется минимальным (кратчайшее связное дерево). Если в сформулированном ранее алгоритме построения обычного остова рассматривать рёбра в порядке возрастания их весов, то будет построен минимальный остов.
Пример 3.11.
Рис.3.11
Алгоритм построения системы независимых циклов графа
1. Строится произвольный остов графа. В исходном графе отмечаются рёбра, не включенные в остов.
2. Выбирается очередное отмеченное ребро и строится цикл, содержащий это ребро и рёбра остова. Рассмотренное ребро отмечается и, если есть ещё не отмеченные рёбра, то выполняется пункт 2, иначе - пункт 3.
3. По формуле Эйлера (3.2) производится проверка числа построенных циклов.
Пример 3.12.
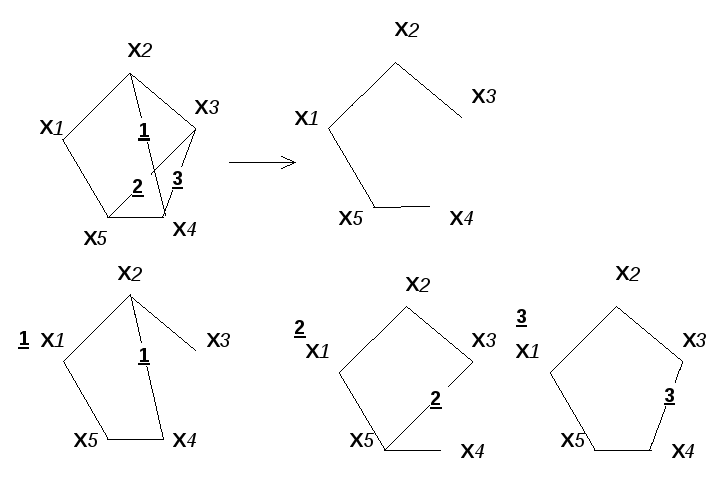
Рис 3.12
1)(X2,X4)(X4,X5)(X5,X1)(X1,X3);
2)(X3,X5)(X5,X1)(X1,X2)(X2,X3);
3)(X3,X4)(X4,X5)(X5,X1)(X1,X2)(X2,X3).
3.6. Алгоритм кратчайшей раскраски графа
Раскраска представляет собой маркирование вершин графа таким образом, чтобы у смежных вершин маркеры не совпадали. Вместо красок используются числа 0, 1, 2… Условие оптимальности раскрашивания - использование минимального числа красок . Это число называется хроматическим числом графа.
Граф, который можно представить на плоскости без пересечения его рёбер, называется плоским.
Теорема. Для плоских графов 4.
Отметим, что проблема раскраски - алгоритмически неразрешима.
Пример 3.13. Рассмотрим граф G (рис. 3.13). Убедившись в том, что он – плоский (ребро (x1, x5) может быть проведено вне контура (x1, x2, x3, x5)), произведём его раскраску. Имеем: =3 (краски 0, 1, 2).
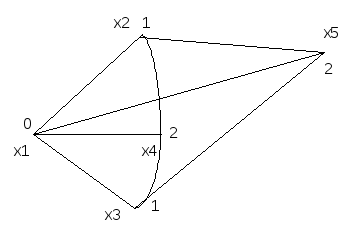
Рис. 3.13
В общем случае строим таблицу для определения максимальных внутренне-устойчивых подмножеств множества вершин графа, т. е. множеств несмежных вершин графа. Строки таблицы – внутренне-устoйчивые множества. Столбцы этой таблицы - номера вершин графа, а последний столбец - имя очередного максимального внутренне-устойчивого подмножества.
Несмежные вершины отмечены в таблице единицами. Далее решается задача построения одного кратчайшего покрытия (методом минимального столбца - максимальной строки). Вершины, принадлежащие каждому подмножеству, вошедшему в найденное кратчайшее покрытие, окрашивается одной краской. Если некоторая вершина принадлежит нескольким вошедшим в покрытие подмножествам, то она в одном остаётся, из остальных исключается. Для нашего примера получим три подмножества: Y1,Y2,Y3, определяющие три краски 0, 1, 2 соответственно.
как показано на рис. 3.13, если x1 покрасить краской 0, то все смежные с ней вершины x2, x3, x4, x5 нельзя покрасить 0. Вершины x2, x4 - смежные, для них необходимы две разные краски (1 и 2); аналогично для x3, x4. Однако вершины x2, x3 - не смежные, и их можно покрасить одной краской.
Таким образом, изображенная на рис. 3.13 раскраска - минимальна.
Дополнительно об использованных алгоритмах можно прочитать в [1, 2]. Элементы теории графов изложены в [3].