Волновой алгоритм построения длиннейшего пути во взвешенном графе

Используется волновой алгоритм построения кратчайшего пути для взвешенного графа со следующими отличиями.

1. В п. 1 волнового алгоритма построения кратчайшего пути присваиваем всем вершинам вес 0, тогда автоматически будут строиться длиннейшие пути.

2. В п. 2 алгоритма полагаем .

П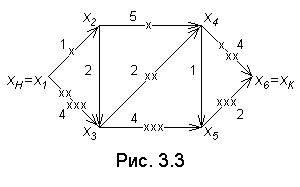ример 3.3. Найти длиннейший путь в графе (рис. 3.3) между вер-

ш

Рассмотрим краткое решение этой задачи.

1. Результаты прямого прохода алгоритма приведены в табл. 3.4.

2. Обратный ход:

инамиx_н и x_к, используя волновой алгоритм.

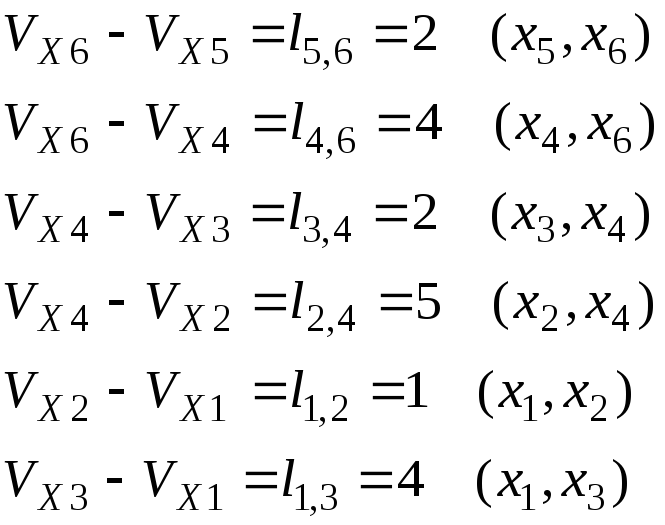
Таблица 3.4

x1	x2	x3	x4	x5	x6	M
0	0	0	0	0	0	1
0	1	4	0	0	0	2,3
0	1	4	6	0	0	3,4
0	1	4	6	8	0	4,5
0	1	4	6	8	10	5,6
0	1	4	6	8	10	6
0	1	4	6	8	10	

Дуги-претенденты: (x₁ x₂), (x₁ x₃), (x₂ x₄), (x₃ x₄), (x₃ x₅), (x₄ x₆), (x₅ x₆).

3. Построены три длиннейшие пути:

L₁: (x₁ x₂),(x₂ x₄), (x₄ x₆); L₂: (x₁ x₃), (x₃ x₄), (x₄ x₆); L₃: (x₁ x₃), (x₃ x₅), (x₅ x₆).

3.3. Нахождение компонент связности

Вершины x_i и x_j слабо связны, если в графе существует путь (x_i, x_j).

Вершины x_i и x_j сильно связны, если существуют пути (x_i, x_j) и (x_j, x_i).

Если в графе нет путей из x_i в x_j и нет обратного пути из x_j в x_i, то вершины x_i и x_j несвязны. Для неориентированного графа имеет смысл только понятие сильной связности.

Компонентой связности называется максимальное подмножество сильно связанных между собой вершин.

Отношение связности рефлексивно, симметрично, транзитивно, т. е. является отношением эквивалентности, и однозначно разбивает множество вершин графа на компоненты связности.

Пример 3.4: Задан граф (рис.3.4). Найти его компоненты связности.

Данный граф может быть разбит на следующие компоненты связности:

1){x1,x2,x3,x4}; 2){x5,x6,x7}; 3){x8}

Между компонентами - только слабая связность: есть пути из вершин 1-й компоненты в вершины 2-й и 3-ей компоненты, а также из вершин 2-й компоненты в вершину 3-ей.

Рис. 3.4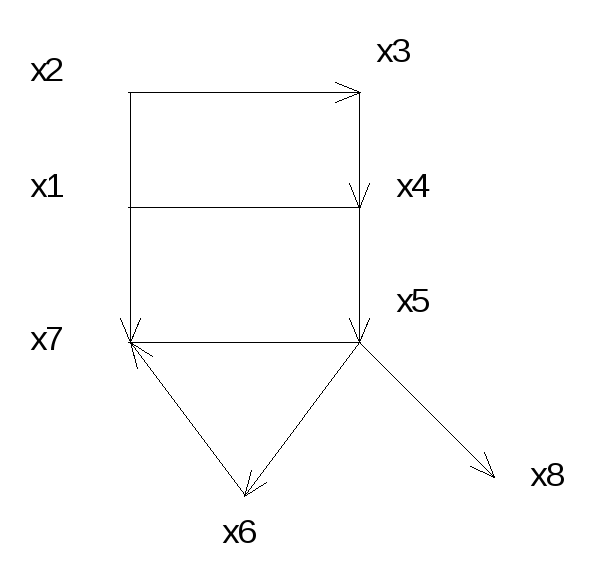

Алгоритм построения компонент связности в неориентированном графе

1. i=0. Все вершины графа не отмечены.

2. i=i+1. Выбираем очередную неотмеченную вершину, отмечаем её и все связанные с нею вершины значением индекса i с помощью распространения волны отметок по ребрам, идущих от уже отмеченных индексом i вершин. Таким образом выделяется i компонента связности. Если есть ещё неотмеченные вершины, то выполняется п.2, иначе выделение компонент связности закончено.

Пример 3.5

Рис. 3.5

Решение:

1. i=0

2. i=1. Отмечаем индексом i=1 вершину x₁ и связанные с ней вершины x₃, x₇ и x₉. Получена первая компонента связности: k₁ {x₁,x₃,x₇,x₉ }

2. i=2. Отметим индексом i=2 вершину x₂ и вершины x₆,x₁₀. Построена вторая компонента связности:k₂ {x₂,x₆,x₁₀}

2. i=3. Отмечаются индексом i=3 вершины x₄ и x₈ . Построена третья компонента связности: k₃ {x₄, x₈ }.

2. i=4. Отмечаются индексом i=4 вершину x₅, которая формирует четвертую компоненту связности – k₄ {x₅}