Отсюда, в частности, имеем при n

и . (4.5)

В более общем случае при n и для любого целого k0

; (4.6)

. (4.7)

4.1.3. Рекуррентные соотношения

Понятие рекуррентных соотношений проиллюстрируем на классической проблеме, поставленной и изученной Фибоначчи около 1200 г.

Фибоначчи поставил свою проблему в форме рассказа о скорости роста популяции кроликов при следующих предположениях. Все начинается с одной пары кроликов. Каждая пара кроликов становится фертильной (fertile – плодовитый) через месяц, после чего каждая пара рождает новую пару кроликов каждый месяц. Кролики никогда не умирают, и их воспроизводство никогда не прекращается. Пусть F_n - число пар кроликов в популяции по прошествии n месяцев и пусть эта популяция состоит из N_n пар приплода и O_n “старых” пар, т.е. F_n = N_n + O_n. Таким образом, в очередном месяце произойдут следующие события:

- старая популяция в (n+1)-й момент увеличится на число родившихся в момент времени n, т.е. O_n+1 = O_n + N_n = F_n;

- каждая старая в момент времени n пара производит в момент времени (n+1) пару приплода, т.е. N_n+1 = C_n.

В последующий месяц эта картина повторяется:

O_n+2 = O_n+1+ N_n+1 = F_n+1,

N_n+2 = O_n+1;

объединив эти равенства, получим рекуррентное соотношение Фибонначи:

O_n+2 + N_n+2 = F_n+1 + O_n+1,

или

F_n+2 = F_n+1 + F_n. (4.8)

Выбор начальных условий для последовательности чисел Фибоначчи не важен; существенные свойства этой последовательности определяются рекуррентным соотношением (4.8). Обычно полагают F₀=0, F₁=1 (иногда полагают F₀=F₁=1).

Рекуррентное соотношение (4.8) является частным случаем однородных линейных рекуррентных соотношений с постоянными коэффициентами:

x_n = a₁x_n-1 + a₂x_n-2 +…a_kx_n-k, (4.9)

где коэффициенты a_i не зависят от n и x₁, x₂, …, x_k считаются заданными.

Существует общий метод решения (т.е. отыскания x_n как функции n) линейных рекуррентных соотношений с постоянными коэффициентами. Этот метод рассмотрим на примере соотношения (4.8). Найдём решение в виде

F_n=crⁿ (4.10)

с постоянными с и r. Подставляя это выражение в (4.8), получим

crⁿ⁺² = crⁿ⁺¹ + crⁿ,

или

crⁿ(rⁿ-r-1)=0. (4.11)

Это означает, что F_n=crⁿ является решением, если либо с=0, либо r = 0 (и отсюда F_n=0 для всех n), а также (и это более интересный случай) если r² - r -1=0, причём константа с произвольна. Тогда из (4.11) следует

r =или r =. (4.12)

Число 1,618 известно как золотое сечение, поскольку с древних времен считается, что треугольник (прямоугольник) со сторонами 1 и имеет наиболее приятные для глаза пропорции.

Сумма двух решений однородного линейного рекуррентного соотношения, очевидно, также является решением, и можно на самом деле показать, что общее решение последовательности Фибоначчи имеет вид

F_n=, (4.13)

где константы с и с’ определяются начальными условиями. Положив F₀=0 и F₁=1, получим следующую систему линейных уравнений:

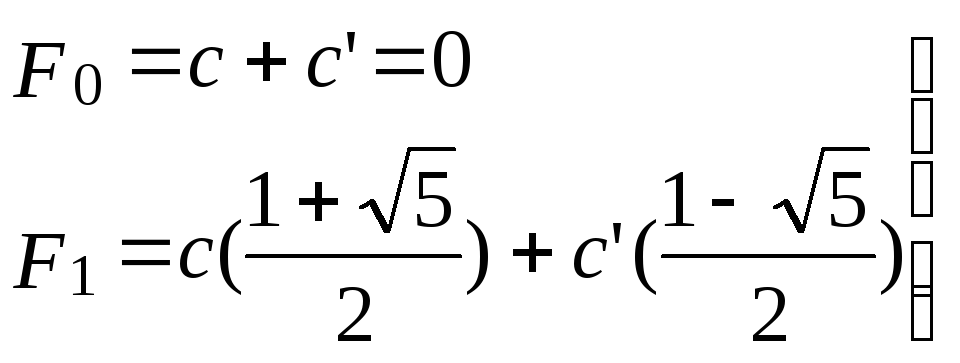, (4.14)

решение которой даёт

c = -c' = . (4.15)

Последовательность Фибоначчи асимптотически растёт как

F_n  , (4.16)

поскольку вторым слагаемым в (4.15) можно пренебречь.